Интегрирование некоторых функций

Учреждение образования «Белорусская государственная

сельскохозяйственная академия»

Кафедра высшей математики

Методические указания

по изучению темы «Интегрирование некоторых функций» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)

Горки, 2013

Интегрирование некоторых функций

1. Интегрирование рациональных функций

Функция вида называется рациональной дробью, если её числитель и знаменатель являются многочленами. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя. Если же степень числителя больше либо равна степени знаменателя, то рациональная дробь называется неправильной.

Так как всякая неправильная дробь может быть представлена в виде суммы многочлена и правильной дроби, то интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби.

Многочлены интегрируются просто. Рассмотрим интегрирование дробей вида _, , которые называются простейшими рациональными дробями.

.

.

Пусть знаменатель дроби имеет действительные корни и может быть представлен произведением множителей вида . Тогда для каждого такого множителя имеет место разложение вида . Таким образом, всякую правильную рациональную дробь можно представить в виде суммы конечного числа простейших дробей. Выполняется это с помощью метода неопределённых коэффициентов.

Пример 1. Проинтегрировать дробь .

Решение. Разложим подынтегральную функцию на простейшие дроби:

. Приравняем коэффициенты при и свободные члены: Решим эту систему уравнений и получим , . Тогда

.

2. Интегрирование некоторых иррациональных функций

Если подынтегральная функция иррациональна, то с помощью замены переменной во многих случаях можно привести её к рациональному виду или к такой функции, интеграл от которой является табличным. Интегрирование при помощи замены переменной, которая приводит подынтегральное выражение к рациональному виду, называется интегрированием посредством рационализации подынтегрального выражения.

Интегралы вида приводятся к интегралам от рациональных функций аргумента t с помощью подстановки , где k – наименьшее общее кратное чисел .

Пример 2. Найти интеграл .

Решение. Наименьшее общее кратное чисел и равно 6. Поэтому нужно применить подстановку . Тогда

. Подынтегральную функцию разложим на простейшие: . Приравняем коэффициенты при и свободные члены: Отсюда найдём Тогда . Таким образом, =. Так как , то . Подставим в полученное выражение:

.

Интегралы вида приводятся к интегралам от рациональных функций с помощью подстановки .

Пример 3. Найти интеграл .

Решение. Выполним подстановку :

.

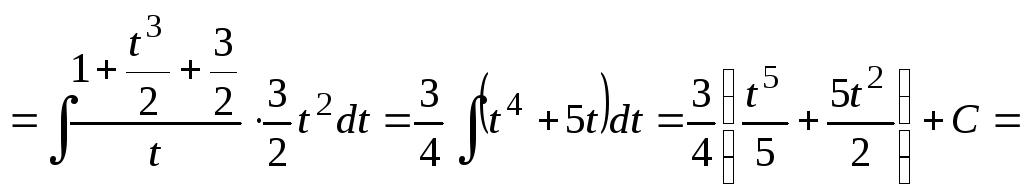
3. Интегрирование выражений, содержащих

тригонометрические функции

Рассмотрим основные случаи интегрирования выражений, содержащих тригонометрические функции.

При нахождении интегралов вида ,

, подынтегральные функции из произ-

ведений преобразовываются в суммы с помощью формул:

,

,

.

В результате полученные интегралы находятся с использованием методов интегрирования и таблицы интегралов. При этом можно использовать формулы и .

Пример 4. Найти интеграл .

Решение. Воспользуемся первой из вышеприведённых формул:

Интегралы вида можно находить довольно просто в следующих случаях.

Если m – положительное нечётное число, то можно отделить первую степень синуса и применить подстановку . Тогда и подынтегральное выражение с помощью тригонометрических формул сведётся к степенным функциям. Если n - положительное нечётное число, то можно отделить первую степень косинуса и выполнить замену . Тогда и подынтегральное выражение с помощью тригонометрических функций тоже сведётся к степенным функциям.

Пример 5. Найти интеграл .

Решение.

.

Пример 6. Найти интеграл .

Решение.

.

Если m и n – неотрицательные чётные числа, то преобразование подынтегральных выражений можно выполнять с помощью формул понижения степени и .

Пример 7. Найти интеграл .

Решение.

.

Подынтегральная функция представляет собой дробь, в числителе которой находится степень синуса, а в знаменателе – степень косинуса, или наоборот. При этом показатели степени или оба чётные, или оба нечётные, т.е. одинаковой чётности.

В этом случае, если в числителе синус, то наиболее подходящей является подстановка . Отсюда , , , .

Если же в числителе косинус, то удобно использовать подстановку . Тогда , , , .

Пример 8. Найти интеграл .

Решение.

.

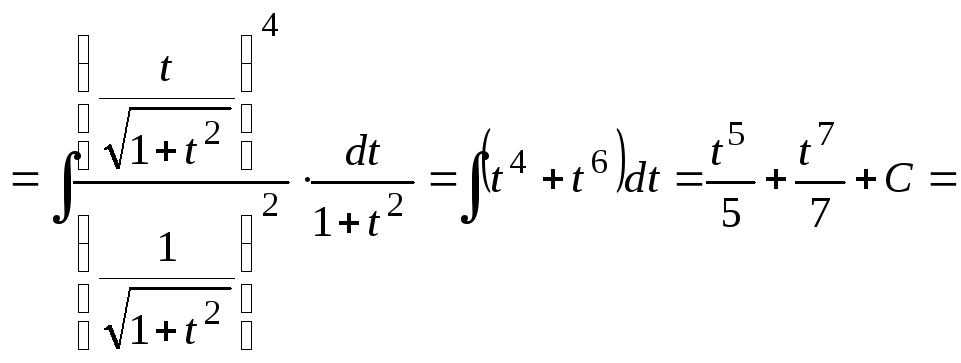
Нахождение интегралов вида сводится с помощью подстановки к нахождению интегралов от рациональных функций. Подстановка называется универсальной тригонометрической подстановкой, которая всегда приводит к результату. В этом случае ,, , , .

Пример 9. Найти интеграл .

Решение. .

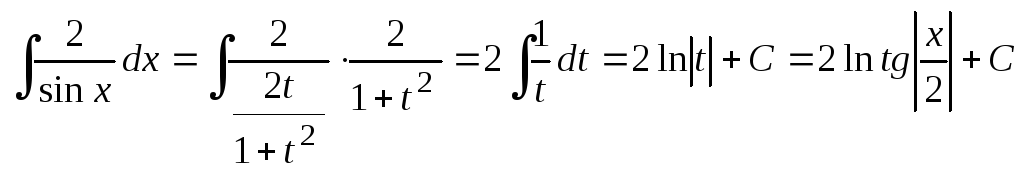Вопросы для самоконтроля знаний

1. Какая функция называется рациональной?

2. Какая рациональная дробь называется правильной, а какая – неправильной?

3. С помощью какой подстановки интегралы вида приводятся к интегралам от рациональных функций аргумента?

4. С помощью какой подстановки интегралы вида

приводятся к интегралам от рациональных функций?

5. Как находятся интегралы вида ,

,

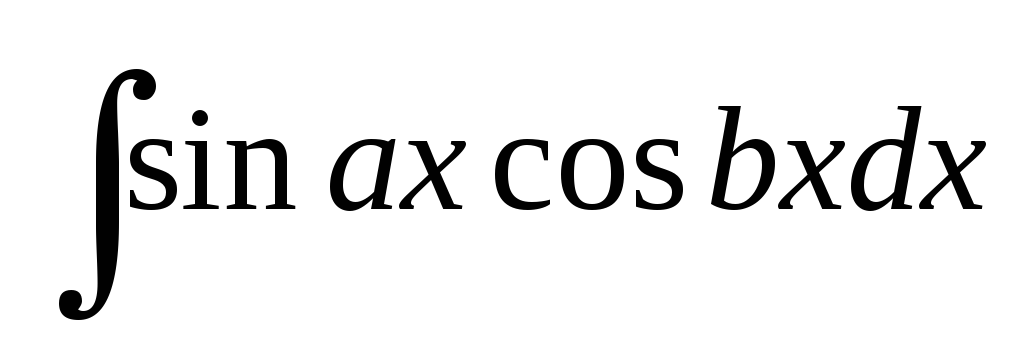6. _{Что называется универсальной тригонометрической подстановкой и когда она используется?}

Задания для самостоятельной работы

1. Найти интегралы от рациональных функций:

а) ; б) ; в) .

2) Проинтегрировать выражения, содержащие тригонометрические функции:

а) ; б) ; в) ;

г) ; д) .

10