Учреждение образования «Белорусская государственная

сельскохозяйственная академия»

Кафедра высшей математики

Методические указания

по изучению темы «Транспортная задача» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)

Горки, 2013

Транспортная задача

1. Постановка транспортной задачи

Транспортная задача является задачей линейного программирования. В общей постановке она выглядит следующим образом.

Имеется m пунктов отправления (поставщиков) с запасами единиц груза. Имеется n пунктов назначения (потребителей) с потребностями . Груз из пунктов отправления должен быть доставлен в пункты назначения. Известны транспортные издержки , связанные с перевозкой единицы груза из пункта в пункт .

Требуется составить такой план перевозок, при котором весь груз из пунктов отправления был бы доставлен потребителям и при этом спрос потребителей был бы удовлетворён, а транспортные издержки были минимальными.

Для разрешимости данной задачи необходимо и достаточно, чтобы сумма запасов была равна сумме потребностей всех пунктов, т.е. . Транспортная задача, в которой выполнено это условие, называется закрытой (или транспортной задачей с закрытой моделью).

Для наглядности транспортную задачу удобно представлять в виде таблицы, которую называют распределительной.

В таблице количество груза, перевозимого от поставщика к потребителю обозначено через .

Матрица называется матрицей тарифов, а числа – тарифами.

Поставщики	Потребители				Запасы груза
			…
			…
			…
…	…	…	…	…	…
			…
Потребность в грузе			…

Матрица называется планом транспортной задачи. Здесь каждое число обозначает количество единиц груза, который надо доставить от i-го поставщика к j-му потребителю. Матрицу Х называют ещё матрицей перевозок.

Общие суммарные затраты, связанные с перевозкой груза, можно представить в виде функции

.

Эта функция называется целевой функцией.

Кроме этого, переменные должны удовлетворять ограничениям по потребностям, по запасам и условиям неотрицательности. Всё это с учётом целевой функции можно записать в виде:

(1)

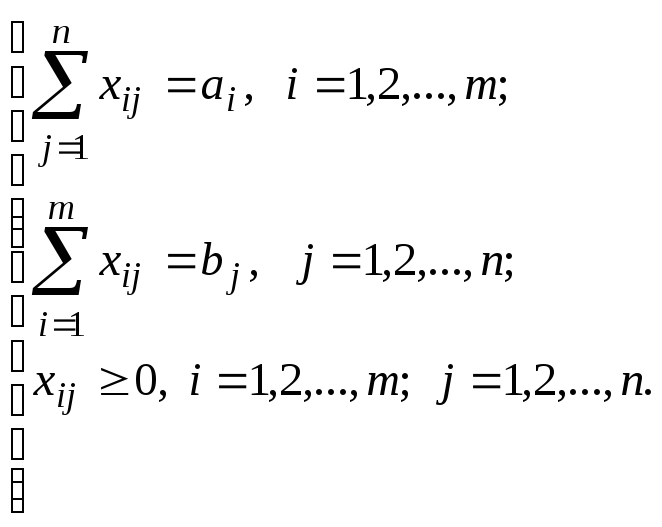(2)

Условия (2) образуют систему ограничений. Любой план, удовлетворяющий этой системе, называется допустимым.

Таким образом, можно математически сформулировать транспортную задачу:

Даны система ограничений (2) и целевая функция (1). Требуется среди множества решений системы найти такой план перевозок, который минимизирует целевую функцию (1).

2. Определение допустимого плана задачи

1. Правило «северо-западного угла». Суть данного правила состоит в следующем. Таблица заполняется, начиная с левого верхнего угла (северо-западного), двигаясь по строке вправо или по столбцу вниз в направлении правого нижнего угла.

Пример 1. Сельхозпредприятия ежедневно выделяют соответственно 30, 40 и 20 ц молока для снабжения пунктов . Стоимость перевозки и потребности пунктов даны в таблице.

Сельхоз- предприятия	Потребители				Наличие
	2	3	5	4	30
	3	2	4	1	40
	4	3	2	6	20
Потребности	20	25	35	10	90

Требуется найти допустимый план задачи.

Решение. Найдём допустимый план задачи с помощью правила «северо-западного угла».

Сельхоз- предприятия	Потребители				Наличие
	2 20	3 10	5	4	30
	3	2 15	4 25	1	40
	4	3	2 10	6 10	20
Потребности	20	25	35	10	90

Затраты на перевозку составят

.

2.2. Правило «минимального элемента». Допустимый план, построенный по правилу «северо-западного угла», обычно оказывается далёким от оптимального. Поэтому в дальнейшем потребуется достаточно много преобразований для достижения оптимального плана. Сократить число таких преобразований позволяет правило «минимального элемента». Суть этого правила в следующем.

Заполнение таблицы начинается с клетки, которой соответствует наименьший элемент из всей матрицы тарифов. Затем остаток по столбцу или строке помещается в клетку того же столбца или строки, которым соответствует следующее по величине значение и т.д.

Пример 2. Решить предыдущий пример, используя правило «минимального элемента».

Решение. Так как наименьшим элементом является , то заполнение таблицы начнём с этой клетки. В клетку с элементом поместим требуемые для пункта 10 ц, затем в клетку с элементом поместим 25 ц, а оставшиеся 5 ц – в клетку с элементом . Таким образом, имеющиеся в наличии 40 ц молока у сельхозпредприятия распределены. Аналогичным образом распределяем запасы молока сельхозпредприятий и .

Сельхоз- предприятия	Потребители				Наличие
	2 15	3	5 15	4	30
	3 5	2 25	4	1 10	40
	4	3	2 20	6	20
Потребности	20	25	35	10	90

Затраты на перевозку составят

.