Министерство образования и науки Украины

Таврический национальный университет им. В.И. Вернадского

Электронный парамагнитный резонанс

Ю.В. Сорокин

2001

Электронный парамагнитный резонанс

Многие из веществ в намагниченном состоянии приобретают способность поглощать энергию электромагнитных волн, падающих на такое вещество. Это поглощение носит резонансный характер, то есть происходит лишь при определенном соотношении между длиной электромагнитной волны и напряженностью постоянного магнитного поля, намагничивающего образец вещества. Явления этого рода получили общее название магнитного резонанса и играют значительную роль в современной физике, химии, биологии и технике как очень эффективное средство исследования строения вещества и как основа для создания весьма важных технических устройств (мазеров, например).

Одна из разновидностей магнитного резонансного поглощения -электронный парамагнитный резонанс, возникающий в результате взаимодействия магнитных моментов электронной оболочки атомов парамагнитных веществ с внешними (постояннымH₀- и высокочастотнымН_)магнитными полями. Сущность этого физического эффекта легко понять, если вспомнить основные сведения о механических и магнитных свойствах атомов и их взаимодействиях, как с внешними магнитными полями, так и друг с другом.

§ I.Магнитные свойства атома

Магнетизм атома порождается тремя причинами:

• орбитальным движением электронов, создающим орбитальный механический 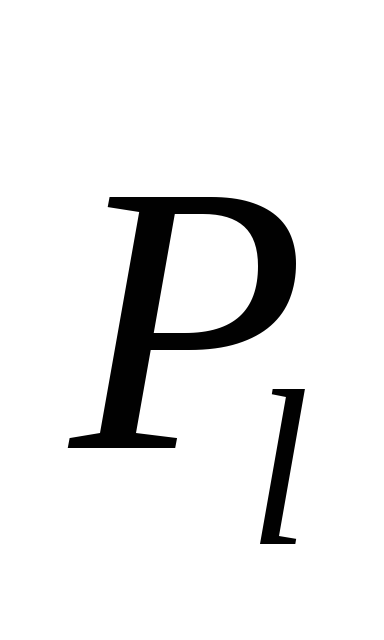и магнитный моменткаждого из них;

• спиновыми свойствами электрона – существованием у него собственных механического и магнитногомоментов;

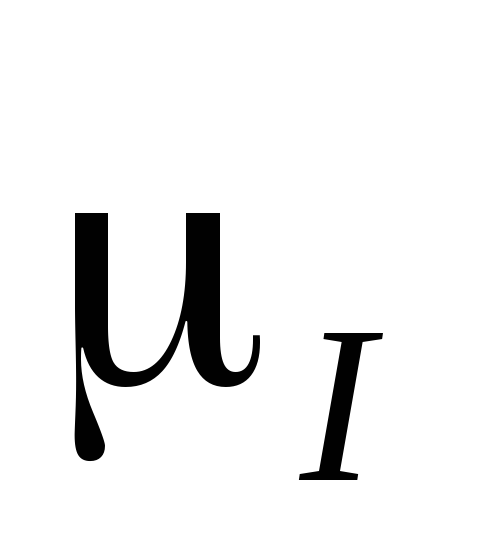• такими же свойствами многих атомных ядер, обладающих собственными механическим и магнитныммоментами.

Обращение каждого электрона вокруг ядра представляет собой аналог кругового тока силой ,создающего орбитальный магнитный момент

, (1)

где S– площадь контура, обегаемого электроном;

механический момент орбитального движения электрона; l– орбитальное квантовое число, а

(2)

так называемое гиромагнитное отношение орбитального движения электрона¹.

Складываясь векторно, орбитальные магнитные моменты всех электронов атома образуют результирующий магнитный момент всей электронной оболочки:

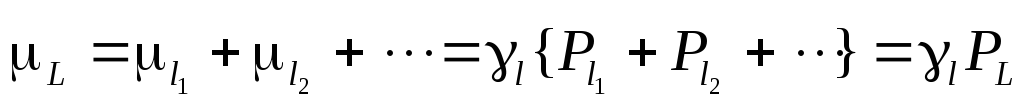(3)

Здесь

– суммарный орбитальный механический момент атом; L –орбитальное квантовое число атома.

Спиновый магнитный момент электрона связан с его механическим моментомсоотношением

, (4)

где

– спиновый механический момент электрона; s– спиновое квантовое число, а

(5)

– его спиновое гиромагнитное отношение. Оно, как видим, вдвое больше аналогичной величины для орбитального движения:

. (6)

Это обстоятельство получило в свое время название гиромагнитной аномалии и, хотя с современной точки зрения здесь нет ничего аномального, название удержалось до сих пор.

Сумма спиновых магнитных моментов всех электронов оболочки образует результирующий спиновый магнитный момент атома:

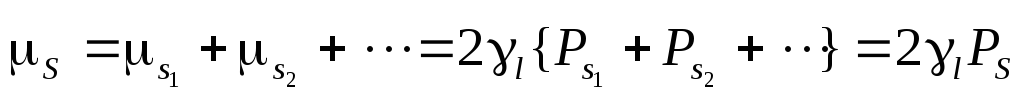(7)

где .

Здесь – суммарный спиновый механический момент атома;S– спиновое квантовое число атома.

Если в формулах (1)и (4)заменить входящие в них величины соответствующими значениями, то получим для орбитального и спинового магнитных моментов электрона соотношения:

, (8)

. (9)

Величина

(10)

называется магнетоном Бора и служит единицей для измерения атомных магнитных моментов.

Квантовые числа lи sпринимают значения:

(11)

где n= 1, 2, 3,… – главное квантовое число.

Это значит, что спиновый магнитный момент электрона приблизительно равен двум магнетонам Бора:

, (12)

в то время как его орбитальный магнитный момент имеет величины разные для различных состояний электрона в атоме, причем при

Заметим, что равенство (12) не имеет большого физического значения, поскольку в эксперименте проявляется не ,aего проекция на заданное полем направление; проекция же эта, как показывают данные, равна по абсолютной величине одному магнетону Бора(см. формулу (14)).

М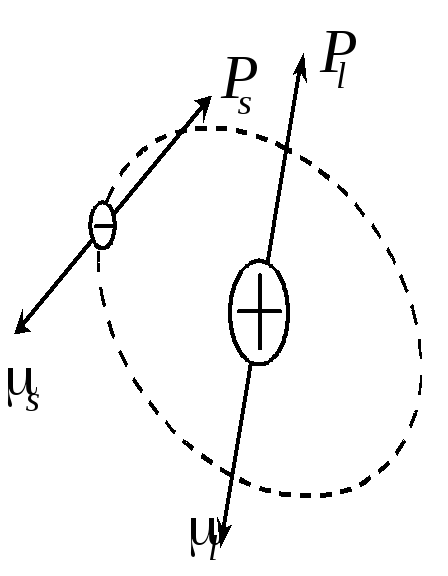агнитные моментыиориентированы антипараллельно соответствующим механическим моментами,так как заряд электрона отрицателен (см. рис. 1).

Рис. 1. Механические и магнитные моменты электрона в атоме

Направления и. относительно друг друга (так же, как направления квантовых векторов вообще относительно заданной оси в пространстве) определяются правилами пространственного квантования: можно точно указать значение проекции квантовоговектора на заданную ось, но нельзя одновременно с тем определить другие компоненты этого вектора. Проекции орбитального и спинового механических и магнитных моментов электрона на ось, заданную направлением постоянного намагничивающего поля,соответственно равны:

, (13)

, (14)

где – орбитальное магнитное квантовое число электрона;– его спиновое магнитное квантовое число.

Таким образом, орбитальные механический и магнитный моменты имогут относительно поля принимать 2l+1различные ориентации, а их проекциииимеют 2l+1возможные значения.

Проекции вектора направлены либо вдоль,либо против него и равныисоответственно.

Сумма результирующих орбитального и спиновогомагнитных моментов атома определяет его результирующий магнитный момент:

. (15)

Поскольку полный механический момент атома равен

, (16)

где

, (17)

(j– внутреннее квантовое число атома), то из (15)и (16)следует, что векторсоставляет с векторомугол, отличный от 180(следствие гиромагнитной аномалии).

Схема сложения моментов ив результирующий магнитный моментвсей электронной оболочки представлена на рис. 2. (в избранном на рис. 2масштабе длина вектораравна длине вектора;в силу гиромагнитной аномалии в этом масштабе длина вектора, вдвое больше длины.).

Рис. 2. Сложение механических и магнитных моментов электронной оболочки атома

Так как вся система векторов вращается вокруг оси совпадающей с направлением вектора , то физическое значение имеет не вектор,а только его слагающая. Векторназывается эффективным магнитным моментом атома или просто магнитным моментом атома.

Таким образом, эффективный магнитный момент атома антипараллелени численно равен

. (18)

Несложные вычисления (см. рис. 2)дают:

, (19)

где

(20)

– так называемый фактор Ланде, или фактор спектроскопического расщепления электронной оболочки атома. Из (20)следует, что величина фактора Ланде зависит от состояния атома. По величине этого множителя можно сделать качественные заключения о происхождении магнетизма данного атома: если,то это возможно приS = 0,но тогда_S= 0,и магнетизм создается только за счет орбитального движения электронов. Если же(точнее 2,00238),то это возможно при_L =0, но тогдаL = 0,и магнетизм имеет чисто спиновое происхождение. Разумеется, возможны и промежуточные случаи.

В случае же конденсированных веществ, когда взаимодействие данного атома с атомами вещества может быть значительным, g-фактор по своей величине может отличаться оттого, что дает формула (20).Эти различия дают возможность судить как о характере взаимодействия атомов, таи и о природе магнетизма данного вещества.

Для получения полного, а, следовательно, точного значения магнитного момента атома в целом, к величине (15)нужно добавить векторное значение магнитного моментаатомного ядра:

. (21)

Собственный магнитный момент ядра равен

, (22)

где _I –гиромагнитное отношение ядра, равное

; (23)

–ядерный фактор спектроскопического расщепления (или фактор Ланде); m_p– масса протона;– собственный момент количества движения ядра, численно равный

, (24)

I –спиновое квантовое число ядра.

Подставляя формулы (23)и (24)в (22),определим величину собственного магнитного момента ядра:

. (25)

Величина

(26)

называется ядерным магнетоном и служит единицей для измерения магнитных моментов ядер².

Поскольку приблизительно в 210³раз меньше(магнетона Бора), то ядерные магнитные моменты приблизительно в210³раз меньше электронных (g_Iи I^*имеют значения порядка единицы). Поэтому ядерный магнетизм часто можно не принимать во внимание. Однако «часто» не означает «всегда»: в ряде случаев пренебрегать ядерным магнетизмом нельзя; так, в электронном парамагнитном резонансе он обуславливает возникновение сверхтонкой структуры резонансных линий поглощения. Более того, существование ядерных магнитных моментов обеспечивает возможность очень важной разновидности магнитного резонанса – ядерного.