Лабораторна робота №6

Оцінка надійності безпілотних літальних апаратів в процесі їхньої експлуатації.

1. Мета роботи

1) Вивчити і одержати навички побудови математичних моделей надійності систем з відновленням.

2) Застосувати методики оцінки надійності ремонтованої системи і розробити програмний комплекс розрахунку показників надійності ремонтованої системи з урахуванням надійності і відновлення її елементів.

3) Проведення обчислювальних експериментів.

2. Постановка завдання

Для проведення випробувань засобів протиповітряної оборони на полігоні є десять безпілотних літальних апаратів (повітряних мішеней). В процесі їхньої експлуатації з ладу виходять в середньому від 1 до 4 мішеней на місяць. На проведення ремонту однієї повітряної мішені потрібно в середньому від 15 до 90 днів.

Потрібно оцінити надійність виконання повітряними мішенями поставлених завдань і ступінь готовності наявних повітряних мішеней протягом місяця їхньої експлуатації.

3. Методика розрахунку надійності системи з урахуванням відмов її елементів.

Розглянемо два випадки відновлення елементів системи:

1. Коли при відмові елемента система вимикається, відбувається ремонт цього елемента, і система знову включається.

2. Ремонт елементів, що відмовили, відбувається в процесі функціонування системи.

Перший випадок.

Припустимо, що відмова більш ніж одного елемента неможливий, тому що потік відмов є пуасоновским потоком.

Нехай μ - інтенсивність потоку відновлення першого елемента. Якщо система складається з елементів з однаковими интенсивностями відмов елемента λ, то інтенсивність відмови системи визначається по формулі виду:

λc = n λ. 1)

(

Система може перебувати в наступних станах: E₀ – система працездатна; E₁ – система виключена, відбувається ремонт елемента, що відмовив. Граф зв'язку станів буде мати вигляд:

Рис.1. Граф зв'язку станів.

У цьому випадку функція надійності визначається по наступній формулі:

.

(2)

Коефіцієнт готовності системи обчислюється в такий спосіб:

.

(3)

Ймовірність того, що в інтервалі часу [0,t] система буде працювати без перерви на ремонт, визначається як:

.

(4)

Другий випадок.

Нехай μ - інтенсивність потоку відновлення одного елемента. Розглянемо стан системи, що враховує число несправних елементів:

E₀ – всі елементи справні;

E₁ – перший елемент ремонтується, ( n-1) елементів працюють;

…

E_{k -}k елементів ремонтується, ( n-k) елементів працюють;

…

E_n – n елементів ремонтується.

При побудові моделі надійності будемо мати на увазі наступний факт: при відмові k елементів системи інтенсивність потоку відновлень становить:

μ(k)=kμ,  k=1,2,…,n...

(5)

Граф зв'язку наведених станів представлений на рис.2.

Рис.2. Граф зв'язку станів.

Математична модель завдання записується в такий спосіб:

.	(6)
.	(7)
.	(8)

Вирази (6)-(8) звуться рівняння «загибелі і розмноження».

Функція надійності системи p(t)=P₀(t) визначається шляхом чисельного рішення завдання (6)-(8).

На основі рівнянь (6)-(7) можна одержати стаціонарні (сталі) значення ймовірностей:

(9)

Для цих цілей в рівняннях (7) припускають, що 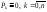. Отримана система лінійних алгебраїчних рівнянь вирішується разом з перетвореною умовою (7) виду:

.

(10)

За знайденим значенням можна знайти середнє число несправних елементів у системі (математичне очікування числа несправних елементів):

,

(11)

коефіцієнт готовності визначається в такий спосіб:

.

(12)
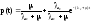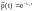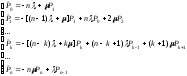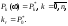
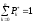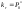