Антонов - Прикладная механика - 2004

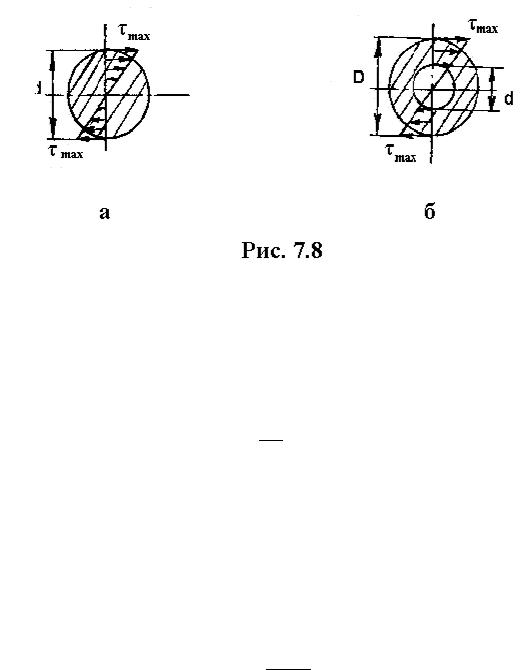
91

где максимальное значение радиуса ρmax = D/2, c = (d/D) ≤ l.

Условие статической прочности вала при кручении имеет вид:

τmax = M z ≤ [τ],

Wp

где [τ] – допускаемое касательное напряжение.

Ниже будет показано, что для малоуглеродистой стали [τ] =

(0,5 ÷ 0,6)[σ].

Из выражения (7.2) найдем угол закручивания вала:

ϕ = ∫M z dz .

L GI p

Входящее в эту формулу произведение GIρ называется жестко-

стью вала при кручении. При Mz = const и GIρ = const получим формулу для определения угла закручивания вала постоянного сечения:

92

ϕ= M z l . GI p

Для обеспечения требуемой жесткости вала при кручении необходимо выполнить условие:

где [Θ] - допускаемый относительный угол закручивания вала.

[Θ] = (5 ÷ 22) 10 -3 [1/м] – для оборудования общего назначения.

Полученные соотношения позволяют производить построения эпюр углов закручивания.

7.4. Потенциальная энергия при кручении

Рассмотрим с энергетической точки зрения процесс статического нагружения вала постоянного сечения и длиной 1 крутящим моментом Мk. При статическом нагружении (медленном изменении нагрузки по времени) упругой системы работа внешних сил преобразуется в потенциальную энергию деформации.

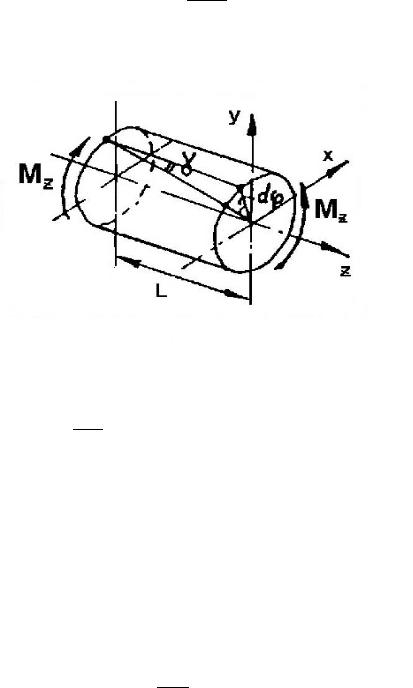
Внашем случае на элементарном уровне для элемента объема, выделенного внутри вала: dU=Mzdφ (рис. 7.10).

Вобласти упругих деформаций угол закручивания вала и крутящий момент Mz связаны линейной зависимостью:

93

ϕ= M z l , GI p

Рис. 7.10

отсюда находим dϕ = GIl dM z .

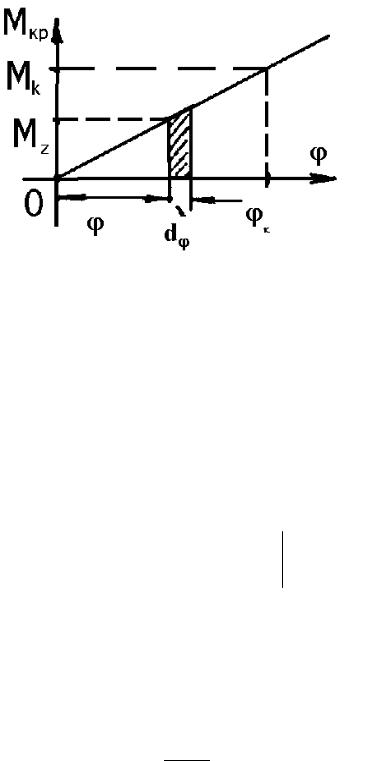
Рассмотрим далее графическую зависимость между моментом и углом закручивания (рис. 7.11). Из построения и из предыдущего соот- но-шения следует, что приращение потенциальной энергии связано с прира-щением угла закручивания в результате приложения крутящего момента следующим образом:

dU = GIl p M z dM z .

94

Рис. 7.11

Далее необходимо проинтегрировать последнее соотношение. Потенциальная энергия, накопленная рассматриваемым валом при воздействии момента Мk, равна:

Mk

Если крутящий момент изменяется по длине бруса, т.е. M(z), да и брус имеет переменное сечение, то полная потенциальная энергия равна интегралу:

= M 2 dz U ∫ z .

L 2GI p

95

7.5.О рациональном сечении вала

Вряде случаев конструктору предоставляется возможность выбора формы сечения бруса или стержня при различных видах нагружения,

вчастности, при кручении. Рациональным сечением следует считать то, которое обеспечивает наименьший расход материала при соблюдении требуемой прочности и жесткости вала. В качестве критерия рациональности сечения можно выбрать безразмерную величину Wk, названную условно удельным моментом сопротивления при кручении:

Wk =Wp / A32 ,

где Wρ - полярный момент сопротивления, характеризующий прочност-

ные свойства вала; А - площадь сечения, пропорциональная массе материала на единицу длины вала.

По этой характеристике сравним некоторые сечения:

2)сплошное круглое сечение……..... Wk = 0,28

3)круговое кольцо при d/D = 0,5…... Wk = 0,37

4)круговое кольцо при d/D = 0,9……Wk = 1,16

Согласно этим результатам наиболее выгодным является кольцевое сечение с малой толщиной стенок. Это станет ясно, если рассмотреть эпюры напряжений в сечениях.

96

В центральной части сплошного сечения материал напряжен сравнительно мало и его прочностное использование является неполным, в кольцевом же сечении малоэффективная центральная часть отсутствует, и степень использования материала повышается. При наличии полостей внутри валов их используют для подачи масла и других жидкостей в качестве смазывающих компонентов.

7.6. Статически неопределимые задачи

Кручение, как и растяжение, относятся к одномерным задачам, и из шести уравнений равновесия независимым остается только одно уравнение:

∑Мz = 0 – при кручении;

∑Nz = 0 - при растяжении.

И если брус закрепить хотя бы в двух сечениях, то число неизестных опорных реакций будет превышать число уравнений равновесия. Такие задачи называются статически неопределимыми, и для их решения необходимо к уравнениям равновесия добавить уравнения совместности перемещений. Метод решения таких задач, как при растяжении, так и при кручении один и тот же.

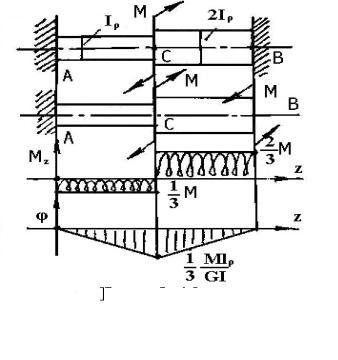
Рассмотрим пример (рис.7.12).

Дано: М, l, Iρ,G = const. Требуется построить эпюры М и

φ.

97

Рис. 7.12

Решение задачи. Отбросим мысленно одну заделку (правую) и ее действие заменим неизвестным моментом MВ, соблюдая принятое правило знаков. Полученная система является статически определимой и называется эквивалентной. В эквивалентной системе найдем и приравняем нулю угол поворота сечения у отброшенной заделки, что выражает условие закепления в исходной системе:

φВА = φВС + φСА = 0,

где

После сокращения устанавливаем, что

0,5МВ + МВ – М = 0,

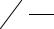
98

Отсюда находим

MВ = (2/3)M, ϕBC = (− 13)MI .

GIp

Найденный момент реакции опоры MВ завершает этап раскрытия статической неопределимости системы. Строим далее эпюру крутящего момента и углов поворота сечений стержня.

Участок I (0 ≤ z1 ≤ l):

M1 = MB – M = (-1/3)M,

ϕ1 = M 1 z1 ;

GIp

при z1 = 0 φ1 = 0, при z1 = l φ = (-1/3)(Ml/GIρ).

Участок II (0 ≤ z2 ≤ l):

M2 = MB = (2/3)M, ϕ2 = M 2 z2 +ϕCA ; 2GIp

при z2 = 0 φ2 = (-1/3)(Ml/GIρ), при z2 = l φ2 = 0.

По результатам расчетов завершаем построение графиков (эпюр) установленных величин на рис. 7.12.

Отметим, что представленный алгоритм расчетов применим и в случае большого числа участков нагруженного стержня, для которых операция метода сил (“РОЗУ”) применяется последовательно от участка к участку. Нумерацию участков целесообразно начинать с незакрепленного конца бруса.

99

8.ИЗГИБ

8.1.Общие сведения

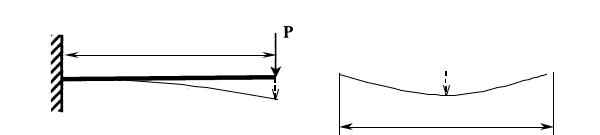
Изгибом называется нагружение и деформация бруса, сопровождаемая искривлением его продольной оси и возникновением в поперечных сечениях бруса изгибающих моментов (рис. 8.1).

a

a

Рис. 8.1.

Изгиб, вызванный поперечной нагрузкой, называется поперечным изгибом. Поперечный изгиб, при котором брус изгибается в плоскости действия нагрузки, называется прямым. Если плоскость изгиба не совпадает с плоскостью действия нагрузки, то изгиб называется косым изгибом. Брус, работающих на изгиб принято называть балкой независимо от того, в каких конструкциях он используется. В химическом оборудовании воздействию изгибающей нагрузки подвержены корпусы аппаратов колонного и барабанного типов, печи для обжига цементного клинкера, валы и оси центрифуг, дробилок, вальцев, различных перемешивающих устройств, трубопроводы, имеющие большую длину и другие элементы аппаратов химической промышленности.

100

Внутренними силовыми факторами при воздействии поперечных сил на балку при изгибе являются перерезывающая (или поперечная) сила Q и изгибающий момент М.

8.2. Эпюры поперечных сил и изгибающих моментов

Эпюры Q и М определяют методом сечений. Знаки поперечной силы Q и изгибающего момента М в сечении соответствуют принятым знакам деформации балки.

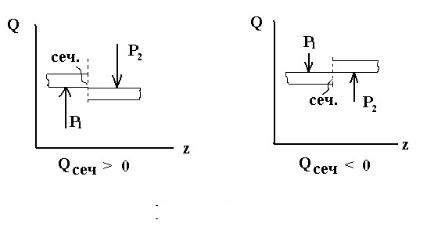
Перерезывающая сила Q вызывает деформации сдвига сечений.

Рис. 10.2

Деформация сдвига считается положительной, если отсеченная часть балки слева от сечения сдвигается вверх, или справа от сечения вниз (рис.10.2).

Перерезывающая сила Qсеч в сечении равна алгебраической сумме внешних поперечных сил Pi , приложенных к балке по одну сторону от сечения. При этом внешняя поперечная сила Pi принимается положи-