1) Только IV;

¹2^{) только IV}и^;II;

²3^{) только I}I^и; ^II;

³4^{) только II;}и III;

5^{4) только I}.^{I и III;}

5) Только I.

⎞

_{11. Если U = sin(x + 2 y 2 − z ) , то значение U ′ в точке M ⎛ π ;0;0⎟ равно:}

^⎜

^{z ⎝ 2 ⎠}

₁

^{1) − ; 2)}

²

₁

^{1) −}

²

; 2)

_{3 2}

_{; 3) 0; 4) 1; 5) .}

^{2 2}

12. Издержки предприятия на изготовление единицы некоторого вида продукции

^{определяются формулой z = x + y − x 2 y + 5 ; где x – затраты капитала, тыс. руб.,}

^{(x>0), y – расходы на оплату рабочей силы, тыс. руб., (y>0). При каких значениях x и}

y издержки производства будут минимальными, если затраты x+y на единицу продукции составляют 3 тыс. руб.:

1) x=1, y=2; 2) x=2.5, y=0,5; 3) x=2, y=1;

4) x=1.8, y=1.2; 5) x=1.5, y=1.5;

^{13. Интеграл} _∫

1) x=1, y=2; 2) x=2.5, y=0,5;

55 xx==11 55 yy==11 55

4) x=1.8, y=1.2; ) . ,5) x=.1;.;5, y=1.5;

^{13. Интеграл ∫}

3) x=2, y=1;

31

_x ² _dx

^{13. Интеграл ∫} _x ³ _{− 1} ^равен:

_{1) ln x} ³ _{−1 + C ; 2)} ² _{ln x} ³ _{−1 + C ; 3) 2 ln x} ³ _{−1 + C ;}

³

₁

_{4) −} 1

_{+ C ; 5)}

_{ln x} ³ _{−1 + C ;}

_(x ³ _{− 1)}^{2 3}

x −

_{1) ln x} ³ _{−1 + C ; 2)} ² _{ln x} ³ _{−1 + C ; 3) 2 ln x} ³ _{−1 + C ;}

³

4) ₋

1

_(x ³ _{− 1)}²

_{+ C} ; 5)

¹ _{ln x} ³ _{−1 + C ;}

³

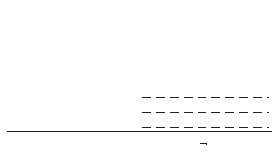
14. Площадь заштрихованной части фигуры, изображенной на чертеже, задана интегралом:

2

¹⁾ _∫ ^{(6 −}

− 3

₂

x ² −

x )d x ^;

²⁾ _∫ ^{(5 −}

− 3

₂

x ² ₎d x ^;

^{3) 2} _∫ ^{(6 −}

0

₂

x ² −

x ₎d x ^;

^{4) 2} _∫ ^{(5 −}

0

x ² ₎d x ^;

2

⁵⁾ _∫ [^{(5 −}

− 3

x ² ) − ⁽ x

^{+ 1 )}]^{d x .}

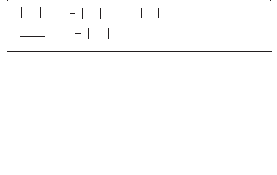
15. Частное решение дифференциального уравнения

15. Частное решение дифференциального уравнения

_{⎛ π ⎞}

^{y ′ ⋅ sin x = y ⋅ cos x}

при

_{y⎜ ⎟ = 1 имеет вид:}

^{⎝ 2 ⎠}

1

_{ощадь заштрихованной части фигуры, изображенной на чертеже, задана}

4. Пл

интегралом:

₂

¹⁾ ∫ ^{(6 −}

^{− 3}

₂

x ² −

^{x )d x ;}

²⁾ ∫ ^{(5 −}

^{− 3}

₂

^{x 2 )d x ;}

³⁾ _{2 ∫ (6 −}

x ² −

_{x )d x} ^;

2

_{1) cos x ; 2) cos x + 1 ; 3) sin x +1 ;}

⁰ _{4) sin x ; 5) − sin x .}

^{4) 2} _∫ ^{(5 − x 2 )d x ;}

2

16. Общим решением дифференциального уравн⁰ения y ′′ = 8 sin⁽2x ⁾ является:

_{5) [(5 −}

_{x 2 ) − ( x}

_{+ 1 )]d x .}

1 2

1) _{C ⋅ sin}(_2x ) _{+ C}

; ²⁾ − 2 ⋅ sin⁽2x ⁾ + C₁ ⋅ x_∫ + C ₂ ^; ₃₎

^{− 3}

_{15. Частное решение дифференциального уравнения}

1 2

^{1) C ⋅ sin(2x ) + C}

^{; 2) − 2 ⋅ sin(2x ) + C}₁ ^{⋅ x + C} ₂ ^{; 3) C ⋅cos(2x) +C ;}

1 2

^{4) 8⋅sin(2x ) +C}₁^{x +C}₂ ^{; 5) −4⋅sin(2x) +C}₁^{x +C}₂ ^.

_{17. Из рядов}

∞

∞

2

∞

_{a) ∑ =} ⁷ⁿ

^{+ 5n} _{; b) ∑}

^n! _{; c) ∑} ¹

_n=1

^{9n2 − n}

n₌₁

100ⁿ

_n=1 n ⋅

n +1

сходятся:

_{1) только a; 2) только с; 3) только b и c; 4) ни один не сходится; 5) только b.}

_{18. При разложении функции y = 1 − 2 ⋅ sin} ² _x

в ряд Тейлора в окрестности точки

^{x = 0 первыми тремя отличными от нуля членами ряда будут:}

_{2 4 3 5 3}

¹⁾ _{2 −} ²

^{2 !}

_{⋅ x} ² ₊ ²

^{4 !}

_{⋅ x} ⁴ _{−. . .} ^{; 2) x} ₋

2

^{1 !}

_{x x}

+

^{3 ! 5 !}

_{− . . .} ^{; 3)} _{1 −} ^x ₊

^{1 !}

^x _{− . . .} ^;

^{3 !}

_{4) 1 −} ^x

² _x ⁴

₊

_{−. . . ; 5) 1 −} ²

_{⋅ x} 2 ₊ ²

4

_{⋅ x} ⁴ _{−. . .}

_{2 ! 4 ! 2! 4 !}

¹⁾_9.^то_С^л_к^ь_о^к_л^о_ь^a_к^;_{о р}²_а⁾_зл^т_и^о_ч^л_н^ьк_ы^о_х^с_п^; _ра³_в⁾_и^т_л^о_ь^л_н^ь_ы^ко_х ^b_др^и_о^c_б^;_ей ⁴_м⁾_о^н_ж^и_н^од_с^и_о^н_ст^н_а^е_в^с_и^х_т^о_ь^ди_з^тс_ч^я_и^;_сел⁵⁾₁^т_,^о₂^л_,^ьк₃^о_{, 5}^b_,^. _7,

11, 13:

₁₎ ^{7 !} _{; 2)} ^{7 !}

_{; 3)} ^{7 !} _{; 4)} ^{7 !}

33

_{; 5)} ^{7 !} _.

^{2 ! 3 !⋅ 4 !}

^{5 ! 2 !⋅ 5 !}

^{4 !⋅ 3 !}

_{18. При разложении функции y = 1 − 2 ⋅ sin} ² _x

в ряд Тейлора в окрестности точки

_{x = 0 первыми тремя отличными от нуля членами ряда будут:}

_{2 4 3 5 3}

¹⁾ _{2 −} ²

^{2 !}

_{⋅ x} ² ₊ ²

^{4 !}

_{⋅ x} ⁴ _{−. . .} ^{; 2) x} ₋

2

^{1 !}

_{x x}

+

^{3 ! 5 !}

_{− . . .} ^{; 3)} _{1 −} ^x ₊

^{1 !}

^x _{− . . .} ^;

^{3 !}

_{4) 1 −} ^x

² _x ⁴

₊

_{−. . . ; 5) 1 −} ²

_{⋅ x} 2 ₊ ²

_{⋅ x} ⁴ _{−. . .}

2 ! 4 !

2! 4 !

19. Сколько различных правильных дробей можно составить из чисел 1, 2, 3, 5, 7,

11, 13:

4

₁₎^{= 7 !} _{; 2)} ^{7 !} _{; 3)} ^{7 !} _{; 4)} ^{7 !} _{; 5)} ^{7 !} _.

2 ! 3 !⋅ 4 !

5 ! 2 !⋅ 5 !

4 !⋅ 3 !

20. В урне 6 белых и 4 черных шара. Из урны вынимают сразу 2 шара.

_{Вероятность того, что оба шара будут белыми, равна:}

_{1) =}^{7 !} _{; 2) =} ^{7 !}

_{; 3) =}^{7 !} _{; 4) =} ^{7 !}

_{; 5) =} ^{7 !} _.

2 ! 3 !⋅ 4 !

5 ! 2 !⋅ 5 !

4 !⋅ 3 !

20. В урне 6 белых и 4 черных шара. Из урны вынимают сразу 2 шара.

Вероятность того, что оба шара будут белыми, равна:

₁₎ ³ _{; 2)} ² _{; 3)} ¹ _{; 4)} ¹ _{; 5) 1 .}

5 3 3 2

₃2₄1. В магазин поступает продукция трех фабрик. Причем продукция первой фабрики составляет 20%, второй – 45% и третьей – 35% изделий. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй

– 2%, и для третьей – 4%. Вероятность того, что оказавшееся нестандартным

21. В магазин поступает продукция трех фабрик. Причем продукция первой фабрики составляет 20%, второй – 45% и третьей – 35% изделий. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй

– 2%, и для третьей – 4%. Вероятность того, что оказавшееся нестандартным изделие произведено на ПЕРВОЙ фабрике, равна:

₁₎ ⁹

1 ₇

_{; 2) ; 3)}

_{; 4)} ⁶ _{; 5)} ¹ _.

₂₃₆ 5

118 29 3

22. График плотности распределения случайной величины Х имеет вид:

Тогда М(X+5)=:

1) 1;

2) 0;

3) 0,5;

4) –1;

_{5) 5.}

k

23. Случайная величина ξ распределена по закону Пуассона

P (ξ = k ) = ^λ

^{⋅ e − λ} _,

k !

где k=0, 1, 2. По результатам наблюдаемых значений 2; 1; 1; 3; 1; 4; 2; 5; 1; 7

_{неизвестный параметр λ этого распределения, равен:}

1) 5; 2) 1,7; 3) 2,7; 4) 3; 5) 7.

35

24. С помощью журнала посещаемости собраны данные о числе пропущенных занятий по математике (за один семестр) у 25 студентов I курса. В итоге получены значения: 2, 5, 0, 1, 6, 3, 0, 1, 5, 4, 0, 3, 3, 2, 1, 4, 0, 0, 2, 3, 6, 0, 3, 0, 1. Значение эмпирической функции распределения F₂₅(3) по данной выборке равно:

1) 11/25; 2) 19/25; 3) 14/25; 4) 5/25; 5)7/27.

25. На товарных станциях A и B имеется по 30 комплектов мебели. Перевозка одного комплекта со станции A в магазины C и D стоит соответственно 2 ден. ед. и

5 ден. ед., а стоимость перевозки со станции B в те же магазины – 4 ден. ед. и 3 ден. ед. Необходимо доставить 20 комплектов мебели в магазин C и 40 комплектов в магазин D. Укажите план перевозок, при котором затраты на транспортировку мебели были наименьшими:

^{1) x}_AC^{=15, x}_AD^{=15, x}_BC^{=23 x}_BD^{=7; 4) x}_AC^{= 0, x}_AD^{=30, x}_BC^{=20 x}_BD^=10;

^{2) x}_AC^{=5, x}_AD^{=20, x}_BC^{=15 x}_BD^=20;

^{5) x}_AC^{=15, x}_AD^{=20, x}_BC^{=5, x}_BD^=20.

^{3) x}_AC^{=20, x}_AD^{=10, x}_BC^{=0, x}_BD^=30;

_{Работу выполнил студент}

_{группа №}

_{ПИН код}

Работу проверил преподаватель

_{Оценка Дата}

1) x_AC=15, x_AD=15, x_BC=23 x_BD=7;

^{2) x}_AC^{=5, x}_AD^{=20, x}_BC^{=15 x}_BD^=20;

^{3) x}_AC^{=20, x}_AD^{=10, x}_BC^{=0, x}_BD^=30;

4) x_AC= 0, x_AD=30, x_BC=20 x_BD=10;

^{5) x}_AC^{=15, x}_AD^{=20, x}_BC^{=5, x}_BD^=20.

I-ВАРИАНТ. 1) 5 2) 5 3) 2 4) 2 5) 1 6) 2 7) 3 8) 5 9) 3 10) 4 11) 4 12) 2 13) 3 14) 4 15) 2 16) 1 17) 1 18) 5 19) 3 20) 1 21) 2 22) 3 23) 2 24) 3 25) 1 II-ВАРИАНТ. 1 - 4 2 - 2 3 - 2 4 - 5 5 - 2 6 - 3 7 - 5 8 - 2 9 - 5 10 - 3 11 - 4 12 - 3 13 - 5 14 - 3 15 - 1 16 - 1 17 - 1 18 - 5 19 - 1 20 - 5 21 - 2 22 - 3 23 - 5 24 - 2 25 - 4 III-ВАРИАНТ. 1)5 2)3 3)2 4)4 5)4 6)2 7)2 8)1 9)3 10)3 11)1 12)3 13)2 14)4 15)1 16)2 17)1 18)2 19)1 20)2 21)1 22)3 23)5 24)5 25)4 IV-ВАРИАНТ. 1-4, 2-4, 3-2, 4-4, 5-5, 6-3, 7-4, 8-5, 9-4, 10-5, 11-3, 12-3, 13-5, 14-1, 15-4, 16-2, 17-2, 18-5, 19-4, 20-3, 21-4, 22-5, 23-3, 24-3, 25-3.