1) Только a и b; 2) сходятся все; 3) только b; 4) только b и c; 5) только a.

1

₁

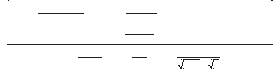
14. Площадь заштрихованной части фигуры, изображенной на чертеже, задана интегралом:

0 4

^{1) −} _∫ ^{( x + 2) 2 d x +} _∫ ^{(4 − x ) d x ;}

_{дисциплина «Математика»}

− 2 0

0 4

_{2) ∫ ( x + 2)} 2 _{dx − ∫ (4 − x )dx ;}

_{15. Частное решение дифференциального уравнения y'=(2y+1) ctg x при y(π/4)=1/2}

_{имеет вид:}

− 2 0

₄

_{1) 2sin2x-1/2; 2) sin2x-1; 3) sin2x+3)1/2∫; 4() 4sin2x+1;}

_{)5) sin2x.;}

− x d x

− 2

_{16. Общим решением дифференциального у}⁰_{равнения y y"-2(}⁴_y')²_{=0 является:}

1) _{y =}

^{1 ; 2)} y =

_{4C) 1∫ ( x ; 2)}

_{dx +3)∫ y}

_{x ) d1x} ;

=

+ C ^;

₊ 2

_{− 2 0}

(4 −

₂

4

^C ₁ ^{x + C} ₂ ^{x + C} ₁ ^C ₁ ^{x + 1}

^{4) y=0} 5) _{y =}

⁵_C⁾ _{( x}

1_∫

_{− 2}

₂ ^+.

_{2 )} ² _{d x} ^.

+

_{x + C 2}

15. Частное решение_∞= дифференциальн_∞о₌ го_n+у₁р₌ авнени_∞я₌ y'=(2y+1) ctg x при y(π/4)=1/2

_{имеет вид: 1 5 1}

_{17. Из 2рядов a) s∑in2}

_{3 ; b) ∑2}

_{; c) ∑2 2}

_{2 2 сходятся:}

_{1) 2sin x-1/2; 2) x-1;}

n=2

₃₎

!

n=1

_n 2; 4) sin _n=1 1; x_n+5₊1);₁sin₊5)xs. in x.

n ln

n

sin

sin x+1/

4)xs+in

6. Общим реш нием дифференциального уравнения y" 2( =0 является:

14⁾ .^тоП^льл^ко^ощ^aад^иь^b;з_еа²ш⁾т^ср^хи^ох^до^яв^та^сн^ян^во^сй^е; ч³а⁾с^тт^ои^льф^ки^ог^bу^;р⁴ы⁾,^тои^лз^ьо^кб^ор_yа^bж^ие_-н^cн^;_yо_')й2 на⁵⁾ ч^те^ор^лт^ье^кж^ое^a,^. задана

_{интегралом: 1}

_{18. При разложении функции y =}

_{в ря0д Тейлора в окр4естности точки 0}

^{2 − x1) −} _∫ ^{( x + 2) 2 d x +} _∫ ^{(4 − x ) d x ;}

− 2 0

0 4

²⁾ _∫ ^{( x + 2) 2 dx −} _∫ ^{(4 − x )dx ;}

− 2

4

³⁾ _∫ ^{( 4 −}

− 2

0

x ) d x ^;

0 4

1) _{y =}

_{1 ; 2) y =}

_{4C) 1∫ ( x ;+ 2)}

_{dx +3)∫ y}

_{= x ) d1x ; + C ;}

^C ₁ ^x

^{+ C} ₂

2

1

_{x +} ⁻_C²

₄

(4 −

2

0

^C 1 ^{x + 1}

_.

^{4) y=0} 5) _{y =}

^5C) 1_∫ ⁽ ₊^x

₂ ^+.

2 ) ² d x

C

2

x + ^{− 2}

_{ференциального уравнения y'=(2y+1) ctg x при y(π/4)=1/2}

^{15. Частное решение}_∞ ^диф₁

_{∞ 5n+1 ∞ 1}

_{и17м.еИетз врияд:ов a) ∑}

_{3 ; b) ∑ ! ; c) ∑ сходятся:}

_{1) 2sin2x-1/2; 2) sin2x-1; 3) sin2x+1/2; 4) sin2x+1; 5) sin2x.}

_n=2 ^{n ln n}

_n=1 ⁿ

_{n=1 n + 1 + n}

_{1) только a и b; 2) сходятся все; 3) только b; 4) только b и c; 5) только a.}

_{16. Общим решением дифференциального уравнения y y"-2(y')}²_{=0 является:}

₁

_{18= . При разложе1нии функции y =}

_{Cв1ряд Тейлора в3о)крестности1 точки ; 0}

1) _{y =}

C x + C

_{; 2) y}

_{=2 − x C ;}

_{y = + C}

C x + 1 ²

^{1 2 x + 1 1}

^{4) y=0} 5) _{y =}

^{C 1} _{+ 2} ^.

^{x + C} ₂

_{∞ 1 ∞}

_{5n+1 ∞ 1}

_{17. Из рядов a) ∑}

_{3 ; b) ∑ ! ; c) ∑ сходятся:}

_n=2 ^{n ln n}

_n=1 ⁿ

_{n=1 n + 1 + n}

1) только a и b; 2) сходятся все; 3) только b; 4) только b и c;

₁

5) то5л)ьтколaь.ко a.

₁₅

^{18. При разложении функции} y =

2 − x

в ряд Тейлора в окрестности точки 0

^{18. При разложении функции} y =

1

_{2 − x}

в ряд Тейлора в окрестности точки

x = 0

первыми тремя отличными от нуля членами ряда будут:

₁₎

2

3

_{1) x x x}

_{x x} 2 _x 3

_{1 x x} 2

2 ⁺ 2 ²

+ _{2 3}

₂

_{+ K} ^{; 2)}

₋

² 2 ²

+ _{2 3}

₂

^{− K ; 3)} ₂ ⁻ ₂ ²

+ _{2 3}

_{− K} ^;

_{4) 1 x x}

_{1 = x}

_{= x .}

₂ ⁺ ₂ ⁺ ₂ ²

^{− K ; 5)} ₂ ⁺ ₂ ²

⁺ ₂ ³

19. В пространстве даны 7 точек, причем никакие 4 из них НЕ ЛЕЖАТ в одной плоскости. Сколько различных плоскостей можно провести через эти 7 точек:

₁₎

₁₎ ^{7 !}

3 !4 !

_{; 2) 4!; 3) 3!; 4)} ^{7 !}

3 !1!

_{; 5)} ^{7 !} _.

4 !1!

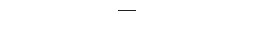
20. Игральная кость бросается один раз. Вероятность того, что появится не менее 5

_{очков, равна:}

1) 1/6; 2) 1; 3) 1/2 ; 4) 2/3; 5) 1/3.

21. С первого автомата на сборку поступает 20%, со второго – 30%, с третьего – 50% деталей. Первый автомат дает в среднем 0,2% брака, второй – 0,3%, третий – 0,1%. Вероятность того, что оказавшаяся бракованной деталь изготовлена на ВТОРОМ автомате, равна:

1) 5/9; 2) 1/2; 3) 2/3; 4) 4/9; 5) 7/9.

22. Если график функции распределения случайной величины Х имеет вид:

то М(X) =:

1) 3/4;

2) 1/4;

3) 3/2;

4) 2/3;

5) ½.

23. В результате пяти измерений длины стержня одним прибором (без математических погрешностей) получены следующие результаты (в мм): 92; 94;

103; 105; 106. Несмещенная оценка длины стержня равна:

1) 106; 2) 105; 3) 94; 4) 103; 5) 100.

24. Интересуясь размером проданной в магазине мужской обуви, мы получили данные по 100 проданным парам обуви, и нашли эмпирическую функцию распределения:

^{⎧ 0 ,}

^⎪

^{⎪ 0 . 04 ,}

^{⎪ 0 . 14 ,}

⎪

если если

если

^{x ≤ 37}

^{37 < x ≤ 38}

^{38 < x ≤ 39}

Обуви 39-го размера было продано:

1) 10;

_⎪ 0 . 29 , если 39 < x ≤ 40 ^{2) 15;}

F₁₀₀ ( x ) = _⎨

_⎪ 0.52,

^⎪ 0.78,

если

_если

40 < x ≤ 41

41 < x ≤ 42

3) 12;

_{4) 23;}

1) 106;

^⎪ 2) 105; 3) 94; 4) 103; 5) 100₅._{) 21.}

1

,

⎩

_⎪ 0.92,

если

42 < x ≤ 43

^⎪ если

x > 43 ¹⁷

25. Фирма производит две модели A и B сборных книжных полок. Для каждого

изделия модели A требуется 3 м² досок, а для изделия модели B – 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю. Для каждого

24. Интересуясь размером проданной в магазине мужской обуви, мы получили данные по 100 проданным парам обуви, и нашли эмпирическую функцию распределения:

^{⎧ 0 ,}

^⎪

^{⎪ 0 . 04 ,}

^{⎪ 0 . 14 ,}

^⎪

₁₀₀ ⎨

^{F ( x ) = ⎪ 0 . 29 ,}

^{⎪ 0.52,}

^{⎪ 0.78,}

^⎪

^{⎪ 0.92,}

⎪

если если если если если если если

^{x ≤ 37}

^{37 < x ≤ 38}

^{38 < x ≤ 39}

^{39 < x ≤ 40}

^{40 < x ≤ 41}

^{41 < x ≤ 42}

^{42 < x ≤ 43}

Обуви 39-го размера было продано:

1) 10;

2) 15;

3) 12;

4) 23;

5) 21.

_⎩ 1 ,

если

x > 43

25. Фирма производит две модели A и B сборных книжных полок. Для каждого изделия модели A требуется 3 м² досок, а для изделия модели B – 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю. Для каждого изделия модели A требуется 12 минут машинного времени, а для изделия B - 30 минут. В неделю можно использовать 160 час. машинного времени. Сколько изделий каждой модели следует фирме выпускать в неделю для получения максимальной прибыли, если каждое изделие модели A приносит 2 ден. ед. прибыли, а каждое изделие B – 4 денежных единиц прибыли:

1) x_A=200 x_B=500; 2) x_A=200 x_B=300; 3) x_A=400 x_B=160;

^{4) x}_A^{=300 x}_B^{=200; 5) x}_A^{=400 x}_B^=300.

_{Работу выполнил студент}

_{группа №}

_{ПИН код}

Работу проверил преподаватель

Оценка Дата

1) xA=200 xB=500;	2) xA=200 xB=300;	3) xA=400 xB=160;
4) xA=300 xB=200;	5) xA=400 xB=300.

Вариант № 3 ^{(id 181527)}

Указания: Все задания имеют 5 вариантов ответа, из которых правильный только один. Номер выбранного ответа обведите кружочком

1 0 0 3

1. Определитель

3 2 1 4

4 1 0 2

3 0 0 1

равен:

1) 0; 2) 2; 3) 6; 4) 1; 5) 8.

1) 0; 2) 2; 3) 6; 4) 1; 5) 8.

_{2. Если A= ⎡2 0 ⎤ и B= ⎡− 1 2⎤ , то AВ+2арBи=ант}

_{⎢ ⎥ ⎢ ⎥}

_⎣^{3 − 2}_⎦

_⎣ ^{2 1}_⎦

1)

Вариант

_{1) ⎡1 2 ⎤}

_{⎡0 4⎤}

_{⎡7 0⎤}

_{⎢ ⎥ ; 2) 0; 3) ⎢}

_{⎥ ; 4) –28; 5) ⎢ ⎥ .}

_⎣^{5 − 1}_⎦

_⎣^{7 0}_⎦

_⎣^{0 4}_⎦

i j k

^{3. Если av = −3 ⋅ r + 6 ⋅ v − 2 ⋅ v , то}

^{av =}

4. Угловой коэффициент "k" и величина отрезка "b" отсекаемого прямой

^{x + 2 ⋅ y + 6 = 0 на оси OY равны:}

1) b=6, k=2; 2) b=3, k=0,5; 3)b=6, k=0.5; 4) b=-3, k=-0,5; 5) b=3, k=2.

5. Уравнение x ² + y ² − 2 ⋅ x − 3 = 0 определяет на плоскости:

1) параболу; 2) прямую; 3) эллипс; 4) окружность; 5) гиперболу.

6. Какое из данных уравнений определяет плоскость:

а) x + 2 ⋅ y − 4 = 0 ; б)

Варианты ответов:

y ² = 4 ⋅ x − 30 ; в) 2 ⋅ x + 3 ⋅ y

+ z = 0 .

1) только а ; 2) только а и в; 3) все; 4) только в; 5) ни одно.

^{71.) Фb=у6н,кkц=и2я; y = 2x) 2b=−34, kо=т0о,5б;раж3а)еbт=м6н, оkж=0ес.5т;во4)(b−=1-;33, ]k=н-а0,м5н; оже5с)твbо=:3, k=2.}

¹⁾ (^{− 3; 5}_]^{; 2)} _[− 4; 5_]^{; 3)} (− 5; 5_]^{; 4)}

^{5. Уравнение x 2 + y 2 − 2 ⋅ x − 3 = 0 определяет на плоскости:}

1) параболу; 2) прямую; 3) эллипс; 4) окружность; 5) гиперболу.

6. Какое из данных уравнений определяет плоскость:

_{а) x + 2 ⋅ y − 4 = 0 ; б)}

_y ² _{= 4 ⋅ x − 30 ; в) 2 ⋅ x + 3 ⋅ y}

_{+ z = 0 .}

Варианты ответов:

1) только а ; 2) только а и в; 3) все; 4) только в; 5) ни одно.

^{7. Функция y = x 2 − 4 отображает множество (−1; 3] на множество:}

^{1) (− 3; 5]; 2) [− 4; 5]; 3) (− 5; 5]; 4)}

1) параболу; 2) прямую; 3) эллипс; 4) окружность; 5) гиперболу.

6. Какое из данных уравнений определяет плоскость:

а) x + 2 ⋅ y − 4 = 0 ; б)

Варианты ответов:

y ² = 4 ⋅ x − 30 ; в) 2 ⋅ x + 3 ⋅ y

+ z = 0 .

1) только а ; 2) только а и в; 3) все; 4) только в; 5) ни одно.

^{7. Функция y = x 2 − 4 отображает множество (−1; 3] на множество:}

^{1) (− 3; 5]; 2) [− 4; 5]; 3) (− 5; 5]; 4)}

1) только а ; 2) только а и в; 3) все; 4) только в; 5) ни одно.

1. Определитель

1 0 0 3

^⎦с

3 2 1 4

4 1 0 2

3 0 0 1

¹

равен:

₁^д₎^и₀^с_;^ципл₂^и₎ ^н₂^а_; ^«М₃^а₎^т₆^е_;^мати₄^к₎ ^а₁^»_{; 5) 8.}

_⎢ ^отобр_⎥^а

⎢

_{27.. ЕФсулникAци=я ⎡2y =0 x⎤ и2 B−=4}^{⎡− 1 2⎤} _{,жтаоеAт +мВ2наBроиж=аенсттв№о 3(− 1; 3] на множество: 1}

_{Указания: ⎣3}

_{− 2В}^⎥ _{е зад⎣ а2ния1⎦имеют 5 вариантов ответа, из которых правильный у}

_{только один. Номер выбранного ответа обведите кружочком}

_{− 3; 5) .}

⎥ ⎢

_{1) ⎡1 2 ⎤}

_{⎡0 4⎤}

_{⎡7 0⎤}

_{; 2) 0; 3)}

_{1 0 0 3}

_{⎥ ; 4) –28; 5) ⎢ ⎥ .}

⎢

_{⎣5 − 1⎦ итель}

_{⎣7 0⎦вен:}

_{⎣0 4⎦}

^{18.. ОПпрредеделел}_lim

x

3. Если

^{x x3 2 1 4 ра} ₁

4 1 0 2

3 0 0 1

1) 0; 2) 2; 3) 6; 4) 1; 5) 8.

_{2.= Если A= ⎡2 0 ⎤ и B= ⎡− 1 2⎤ , то A+2B=}

_{⎢ ⎥ ⎢ ⎥}

^⎣3

₁₎ ⎡^{1 2} ⎤

^{− 2⎦}

^{⎣ 2 1⎦}

_{⎡0 4⎤}

_{⎡7 0⎤}

_{⎢ ⎥} ; 2) 0; 3) _⎢

_⎥ ; 4) –28; 5) _{⎢ ⎥} .

⎣^{5 − 1}⎦ ⎣^{7 0}⎦ ⎣^{0 4}⎦

^{1) (− 3; 5]; 2) [− 4; 5]; 3) (− 5; 5}]^{; 4) (− 4; 5}] ^{; 5) (− 3; 5) . 1}

3. Если

₂

^{8. Предел} _lim ^3x

x → −1

^{+ 9x + 6} _равен:

2x ² − 2

1) -3/4; 2) 3/4 ; 3) -1/4; 4) 3/2; 5) ¼.

_{9. Уравнение касательной к графику функции y=} ¹

x ³ + 1

в точке (0; 1) имеет вид:

¹⁾ x − y + 1 = 0 ^{; 2) x+y-1 = 0; 3)} _{y − 1 = 0} ^{; 4)} _{y + 1 = 0} ^{; 5)} x + y + 1 = 0 ^.

^{3 2 + 9}

^{+ 6} _равен:

^{→ −1}

2 ² − 2

1) -3/4; 2) 3/4 ; 3) -1/4; 4) 3/2; 5) ¼.

_{9. Уравнение касательной к графику функции y=} ¹

x ³ + 1

в точке (0; 1) имеет вид:

^{1) x − y + 1 = 0 ; 2) x+y-1 = 0; 3) y − 1 = 0 ; 4) y + 1 = 0 ; 5) x + y + 1 = 0 .}

10. График какой функции на всем отрезке [a, b] одновременно удовлетворяет трем условиям: y>0; y'< 0; y"> 0?

Варианты ответов:

^В1)^ав^рс^ие^ангр^тыаф^ои^тк^ви^е;^тов:

¹2^{) в}то^сель^гк^ро^афII^и; ^ки;

²3^{) только II}I^;;

³4^{) только III}и^; III;

⁴5^{) только II}и^иI^III. ^;

5) только I и III.

^{11. Если U = ln} (x ² − y + 2z ) ^{, то значение U '} _z ^{в точке M (1;2;2) равно:}

й

(

1) 2/3; 2) 3/2; 3) -1/3; 4) 0; 5) –2.

12. Прибыль П автомобильного завода от производства одного автомобиля определяется формулой П = 0,25 xy-x-y-2, где x – затраты на материалы, млн. руб., (x>0) – затраты на оплату рабочей силы, млн. руб.,(y>0), 2 млн. руб. – постоянные затраты. Значения x и y, при которых прибыль завода максимальна, а суммарные затраты на один автомобиль не превышают 27 млн. руб., равны:

дисциплина «Математика»

_∫

13. Интеграл ^{cos xdx}

sin ² x + 1

равен:

¹⁾ − arctg x + C ^{; 2)} arctg(sin x ) + C

; 3)

₁

(_sin² _{x +1})

_+C ^{; 4) ln sin 2 x +1 + C ; 5)} (sin ² x + 1) + C ^.

14. Площадь заштрихованной части фигуры, изображенной на чертеже, задана

₁^и₄^н_.^те_П^гр_л^а_о^л_щ^ом_ад^: _{ь заштрихованной части фигуры, изображенной на чертеже, задана}

₀

интегралом:

¹⁾ _{2 ∫}

_{[(1 − x ) − (x} ² _{− 5)]dx} ^;

2

0

¹⁾ 2 ⁻_∫³_[⁽1 − x ⁾ − ₍x ² − 5_)]dx ^;

²₂

^{2) −}_∫³_[(x ²

_{− 5) − (1 − x )]dx} ^;

2

^{2) 2}_∫⁰ [^{(x 2 − 5) − (1 − x )}]^{dx ;}

³⁾ _∫ ^{[(x 2 − 5) − (x + 1)]dx ;}

0

³⁾ _∫^{2 [(x 2 − 5) − (x + 1)]dx ;}

−3

⁴⁾ ₍ ^{2 ;}

₂

−3

_∫2 [ ^{1 − x ) − (x − 5)}]^dx

2

^{4) −}_∫³[^{(1 − x ) − (x 2 − 5)}]^{dx ;}

−3

_{5) [(1 − x ) + (x 2 − 5)]dx}

_∫2 ^.

^{5) −}_∫^{3[(1 − x ) + (x 2 − 5)]dx .}

− 3

15. Частное решение дифференциального уравнения (1 + x² ) y' =2 x y при y(0)=1

_{имеет вид:}

1) x²+1; 2) 2x; 3) x³-1; 4) 2x²+3; 5) x² .

_{16. Общим решением дифференциального уравнения y ′′ =}

15. Частное решение дифференциального уравнения (1 + x² ) y' =2 x y при y(0)=1

_{имеет вид:}

_{1) x}²_{+1; 2) 2x; 3) x}³_{-1; 4) 2x}²_{+3; 5) x}² _.

₂

_{16. Общим решением дифференциального уравнения y ′′ =}

x ³

является:

15. Частное решение дифференциального уравнения (1 + x² ) y' =2 x y при y(0)=1

_{имеет вид:}

1) x²+1; 2) 2x; 3) x³-1; 4) 2x²+3; 5) x² .

_{16. Общим решением дифференциального уравнения y ′′ =}

_{= 1 C1}

^{1) − +}

^{x 2 x}

₁

^{+ C 2 ; 2)}

₁

2

^{+ C x + C ; 3) ln x}

^{x 1 2}

^{+ C1 x}

^{+ C 2 x ;}

_{Частное решение дифференциального уравнения (1 + x2 ) y' =2 x y при y(0)=1}

^{415) .− + C x + C ; 5) ln x}

^{имеетxвид: 1 2}

^{+ C1 x + C 2 .}

_{2 3 2 2}

_{1) x +1; 2) 2x;}

_{∞ 3⎡)7xn-+1;1⎤} ⁿ

_{4) 2x∞ +n33; 5∞) x . 1}

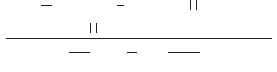
_{17. Из рядов a) ∑ ⎢}

_{⎥ ; б) ∑}

_{n ; в) ∑ ln( ) сходятся:}

^{16. Общим решеnн=и2 е⎣мnд−иф1ф⎦еренциалnь=н1 о3го уравненn=и1яny+′′ = n}

^{1) только b; 2) только с; 3) только b и c; 4) ни один не сходится; 5) только a и c.}

18. При разложении функции y=e^2x+(x-2)² в ряд Тейлора в окрестности точки 0

_{2 и}

_и¹_м⁵_е^._е^Ч_т ^а_в^с_и^т_д^н_:^{ое решение дифференциального уравнения (1 + x}

₁^и₎^м_x^е2₊^ет_1;^в₂^и₎^д:_{2x; 3) x}³_{-1; 4) 2x}²_{+3; 5) x}² _.

1) x²+1; 2) 2x; 3) x³-1; 4) 2x²+3; 5) x² .

_{16. Общим решением дифференциального уравнения y ′′ =}

_д¹_и⁶_с^._ц^О_и^б_п^щ_л^и_и^м_на^ре_«^ш_М^е_а^н_т^и_е^е_м^м_а^д_т^и_и^ф_к^ф_а»^{еренциального уравнения y ′′ =}

^{) y' =2 x y при y(0)=1} _п

1

2

_в

_ц

18. При разложении функции y=e^2x+(x-2)² в ряд Тейлора в окрестности точки первыми тремя отличными от нуля членами ряда будут:

^{x = 0} _п

_{15. Частное решение дифференциального уравнения (1 + x}² _{) y' =2 x y при y(0)=}

_{имеет вид: 2}⁴ _{6 8}

2)

_{1) x3}²_+−12; ² _{x 2−x;}

3)

^2!

x ² +_xK³_-1;_;

²4) 2⁵x⁻²+²3;^{x +}

_x ² _{; 3x)}² _{.5 − 2x +}

5)

2!

_x ² _{+ ;}

^K

^2!

_{16. Общим реш2}⁴_{ением дифференциально6го уравнения y ′′ =}

4) 3 + 2² x +

_x ² _{+ ; 5) 5 − 2}² _{x +}

^K

^2!

_x ² _{+ 2}

^K

^2! _о

19. Сколько различных шестизначных чисел, начинающихся цифрой 2 и о¹к⁹а^.нчи^Св^ка^ою^льщ^ки^охся^рац^зи^лф^ичр^ной^ых5, м^шо^еж^сн^тио^зс^но^ас^чт^на^ыв^хить^чи^из^сец^ли^,фр 1^н, ^а2^ч,^и3^н,^а4^ю, ^щ5,^и6^хсп^яри^цу^ис^фл^ро^ови^йи, ²что^и

_к^о_а^к_ж^а_д^н_а^ч_я^и_ц^ва_и^ю_ф^щ_ра^и_в^хс_о^я_бо^ц_з^и_н^ф_а^р_ч^о_ен^й_и⁵_и^, _ч^м_и^о_с^ж_л^н_а^о_в ^с_т^о_р^с_е^т_ч^а_а^в_е^и_т^т_с^ь_я^и₁^з_р^ц_а^и_з^ф_: ^{р 1, 2, 3, 4, 5, 6 при условии, что е}

^{каждая цифра в обоз}₆^н_!^{ачении числа} ₆^вс_!^{тречается 1 ра}₆^з:_!

_{1) 4!; 2)}

_{6! ; 3)}

_{6!; 4)}

_{6!; 5) 6!}

_{1) 4!; 2) 4 !2! ; 3) 4! ; 4) 2! ; 5) 6!}

_{20. Какова вероятно}⁴_с^!_т²_ь^! _{того, что н}⁴_а^!_{удачу выбранн}²_о^!_{е двузначное число простое и}

_с²_у⁰_м^._м^К_а ^а_е^к_г^ов_ц^а_иф^ве_р^р_р^о_а^я_в^тн_а^ос₅^т_:^{ь того, что наудачу выбранное двузначное число простое и}

₁^с₎^у₁^м_/1^м₀^а_; ^е₂^г₎^о₁^ц_/^и₄₅^ф_;^р₃^р₎^а₁^в_/^н₉^а_; ^5:

_{4) 1/90; 5) 2/5.}

₂¹₁⁾_. ¹_Н^/1_а^0;_ф²_аб⁾ _р¹_и^/4_к⁵_е^;_, ³_и⁾ _з¹_г^/_о⁹_т^; _{овляющей}⁴_б⁾ _о¹_л^/9_т⁰_ы^;_, ⁵⁾_п²_е^/_р⁵_в^._{ая машина производит 25%, вторая –}

₃²₅¹_%^. _,^Н_т^а_ре^ф_т^а_ь^б_я^р_–^ик₄^е₀^,_%^и_в^з_с^г_е^о_х^то_и^в_зд^ля_ел^ю_и^щ_й^е_. ^й_Бр^б_а^о_к^л_п^ты_ро^, _ду^п_к^е_ц^р_и^в_и^ая_со^м_с^а_т^ш_ав^и_л^н_я^а_ет^п_с^р_о^о_о^и_т^з_в^в_е^о_т^д_с^и_т^т_ве²_н⁵_н^%_о ^,_5%^вт_,^о₄^р_%^ая_и^–

всех изделий. Брак продукции составляет соответственно 5%, 4% и

^{23%5%. В, етрроеяттьняо–ст4ь0%тог}₆^о_!^{, что оказавш}₆^и_!^{йся бракованны}₆^м_!

^{болт произведен на ПЕРВОЙ}

_{2%. Вероятность того, что оказавшийся бракованным болт произведен на ПЕРВОЙ}

_{м1)аш4!и; не, равна: 2)}

_{; 3)}

_{; 4)}

_{; 5) 6!}

₁^м₎ ^а₂^ш_5/^и₆^н₉^е_;^{, равна:} _{2) 8}4_/2!2₇₃!_{; 3) 1}4_/3!_{; 4) 1}2₄!_{0/273; 5) 1/20.}

2¹0⁾. ²К^5/а⁶к⁹о^;ва вероя²т⁾н⁸о^/с²т⁷ь^3;того, чт³о⁾ н¹а^/3у^;дачу выбр⁴ан⁾ н¹о⁴е^0/2д⁷в³у^;значно⁵е⁾ ч¹и^/2с⁰л^.о простое и

_{2су2м. Емсалеигослцуичфайрнрааявнвеал5и:чина X задана плотностью распределения}

_{22. Если случайная вел( иx ч−1и)н2 а X задана плотностью распределения}

_{1 − 2}

_{f ( x ) = 1 e −} ^{( x8−1)} _{, то М(3X+3)=:}

_{f ( x ) = 2 2π e}

⁸ _{, то М(3X+3)=:}

п

_1)=0,3; ^{2 2}₂₎^π_{4; 3) 6; 4) 3; 5) 5.}

^{1) 0,3; 2) 4; 3) 6; 4) 3; 5) 5.}

21. На фабрике, изготовляющей болты, первая машина производит 25%, вторая –

35%, третья – 40% всех изделий. Брак продукции составляет соответственно 5%, 4% и

2%. Вероятность того, что оказавшийся бракованным болт произведен на ПЕРВОЙ

машине, равна:

1) 25/69; 2) 8/273; 3) 1/3; 4) 140/273; 5) 1/20.

22. Если случайная величина X задана плотностью распределения

_{( x −1) 2}

f ( x ) =

_{1 −}

_e ⁸

2 2π

, то М(3X+3)=:

1)=0,3; 2) 4; 3) 6; 4) 3; 5) 5.

_{1) 0,3; 2) 4; 3) 6; 4) 3; 5) 5.}

_{23. Случайная величина ξ распределена по нормальному закону с параметрами а и b и}

¹ _{имеет следующие результаты наблюдаемых значений 35; 15; 5; 25; 5. Значение}

_{параметра распределения а этой случайной величины равно:}

1

дисциплина «Математика»

24. Из текущей продукции автомата, обрабатывающего ролики диаметром 20 мм, взята выборка объемом 100 штук. Ролики измерены по диаметру микрометром с ценой деления 0,01 мм. По данным отклонений от номинального размера диаметра построена гистограмма частот:

Сколько роликов имеют отклонение x от номинального размера диаметра, удовлетворяющее неравенству

0.04<x<0.08:

1) 74;

2) 60;

3) 34;

4) 26;

5) 46.

25. Для изготовления изделий N1 и N2 имеется 100 кг металла. На изготовление одного изделия N1 расходуется 2 кг металла, а изделия N2 – 4 кг. Укажите план производства, обеспечивающий получение наибольшей прибыли от продажи изделий, если отпускная стоимость одного изделия N1 установлена 3 ден. единицы, а изделия N2 - 2 ден. единицы, причем изделий N1 требуется изготовить не более 40, а изделий N2 – не более 20:

^{1) x}₁^{=30, x}₂^=25;

^{2) x}₁^{=37, x}₂^=31;

^{3) x}₁^{=42, x}₂^=18;

^{4) x}₁^{=40, x}₂^=5;

^{5) x}₁^{=30, x}₂^=15;

_{Работу выполнил студент}

_{группа №}

_{ПИН код}

_{Работу проверил преподаватель}

_О¹⁾_ц^x_ен1⁼_к³_а^{0, x}2^=25;

^{2) x}₁^{=37, x}₂^=31;

^{3) x}₁^{=42, x}₂^=18;

_{Работу выполнил студент}

Дата

^{4) x}₁^{=40, x}₂^=5;

^{5) x}₁^{=30, x}₂^=15;

27

группа №

ПИН код

_{Вариант № 4} (id 721527)

_{Указания: Все задания имеют 5 вариантов ответа, из которых правильный}

в бланке для ответов

только один. Номер выбранного ответа обведите кружочком^. .

_{25 вопросов на 90 минут.}

_{1. Определитель}

_равен:

4	2 6 7
1	0 3 2
0	0 1 0

^{− 2 0 1 0}

^{1) 4; 2) 2; 3) 0; 4) -8; 5) 5.}

_{1) 4; 2) 2; 3) 0; 4) -8; 5) 5.}

_{2. Если A= ⎡1}

_{− 1⎤}

_{и B= ⎡0 1⎤ , то 3A + B=:}

_{⎢ ⎥ ⎢ ⎥}

^⎣1

^{1) 0 2)}

^{− 1⎦}

^{⎣1 0⎦}

⎢

_{1) 0 2) ⎡1 0 ⎤ ; 3) –1; 4) ⎡3}

_{− 2⎤ ; 5) ⎡3}

_{− 2 ⎤ .}

⎦

⎢

⎦

⎢

⎦

_⎣^{2 − 1⎥}

_⎣^{4 − 3⎥}

_⎣2 − 1 ^⎥

^{3. Если a = −10i + 2 j + 11k , то a =K}

^{1)-15; 2) 15; 3)}

^{1)-15; 2) 15; 3)} 23 ^{;4) 243); 235; ) 25. ) 2.}

Вариант № 4

_дУ_ик_са_цз_иа_пн_ли_ия_н: _{а «Ма}В_тс_ее_маза_тд_иа_кн_аи_»я имеют 5 вариантов ответа, из которых правильный только один. Номер выбранного ответа обведите кружочком в бланке для ответов.

_{25 вопросов на 90 минут.}

⁴_1. ^У_О^г_п^л_р^о_е^в_д^о_е^й_ли^к_т^о_е^э_л^ф_ь^{фициент "}_р^k_а^"_в^и_ен^в_:^{еличина отрезка "b", отсекаемого прямой 3x+2y-6=0,}

1 0 3 2

^{на оси ординат рав4ны2 : 6 7}

1) b=4, k=3; 2)₀b=₀-4₁ , ₀k=2; 3) b=4/3, k=2/3; 4) b=3, k=-1.5; 5) b=-4, k=3.

^{− 2 0 1 0}

^{51.) 4; 2) 2; 3) 0; 4) -8; 5) 5.}

_{2. Если A= ⎡1}

_{− 1⎤}

_{и B= ⎡0 1⎤ , то 3A + B=:}

Каноническое уравнение окружности,

_{⎢ ⎥ ⎢ ⎥}

_{⎣1 − 1⎦}

_⎣1 0_⎦

_{Вариант}^по_№^ка₄^{занной на рисунке, имеет вид:}

_{1) 0 2) ⎡1 0 ⎤ ; 3) –1; 4)}

_{; 1) ( x +51))}2 _{+ y 2 =.1 ;}

^⎡3

^{⎢ ⎥} ⎢

^{− 2⎤}

⎥

^{⎡3 − 2 ⎤}

⎢ ⎥

Указания:_⎣2

^{− 1}_⎦ ^{Все задания имею}_⎣^т4 ⁵− 3^в_⎦ ^ар₂^и₎^{антов о}_⎣2^тве−^т1^а_⎦^{, из которых правильный}

только один. Номер выбранного ответа обведите кружочком в бланке для ответов.

₃²_.⁵_Е^в_с^о_л^п_и^ро_a^с₌^ов₋^н₁^а₀⁹_i ⁰₊ ^м₂^и_j^н₊^у₁^т₁^. _{k , то a =K}

_{1. Определитель}

_{4 2 6 7}

_равен:

^{1)-b1=54; , k2=)31; 5; 32)}₁^b=2₀^-34₃^,;₂^{k4=) 2;3; 53) 2b.=4/3, k=2/3; 4) b=3, k=-1.5; 5) b=-4, k=3.}

0 0 1 0

_{45. Угловой коэффи}⁻ _ц² _и⁰_ен¹ _т⁰ _{"k" и величина отрезка "b", отсекаемого прямой 3x+2y-6=0,}

_н¹_а^{) 4}_о^;_{си ор}²_д⁾_и²_н^;_{ат р}³_ав⁾ _н⁰_ы^; _:

4) -8; 5) 5.

Каноническое уравнение окружности,

_{12). Еb=сл4и, kA==3;⎡1}

_{− 1⎤2) иb=B-=4,⎡}0_k=21_{⎤; , то 3)Ab=+4B/3=,:k=п2о/к3а;з4а)нbн=о3й, нkа=р-1и.с5у; нке5,)иbм=е-е4т, kв=ид3.:}

_{⎢ ⎥ ⎢ ⎥}

^{⎣1 − 1⎦}

^{⎣1 0⎦}

¹⁾ _{( x + 1)}² _{+ y} ² _{= 1} ^;

^{51.) 0 2) ⎡1 0 ⎤ ; 3) –1; 4)} ⎡³

^{− 2}⎤ ^;

^{2) x 2 +} (^{y + 1})^{22 = 1 ;}

^{⎢ ⎥} ⎢ ⎥

5) _⎡3

⎢

⁻ ⎤ ^.

⎥

_⎣2 − 1_⎦

_⎣4 − 3_⎦

^{Канониче}⎣^{2ско−е1} ⎦

уравнение окружности,

^{3. Если a = −10i + 2 j + 11k , то a =K}

^{1)-15; 2) 15; 3) 23 ;4) 23; 5) 2.}

^п3)ок(^{аxз−ан1})^н2о+й(^{нyа−р1и})^{2су=н1к;е, имеет вид:}

^{x + 1}) ⁺ (^{y + 1}) ^{= 1}

^{14) (( x + 12)2 + y 2 =21 ; ;}

^{25) ( x + 1)2 + (y − 1)2 = 1 .}

4. Угловой коэффициент "k" и величина отрезка "b", отсекаемого прямой 3x+2y-6=0,

на оси ординат равны:

1) b=4, k=3; 2) b=-4, k=2; 3) b=4/3, k=2/3; 4) b=3, k=-1.5; 5) b=-4, k=3.

₆⁵_.^. _{Даны уравнения плоскостей: а) 2x+3y+z-1=0; б) x-3y+4z=0; в) y+z+2=0.}

Через начало координат проходят:

Каноническое уравнение окружности,

_{показанной на рисунке, имеет вид:}

^{1) ( x + 1)2 + y 2 = 1 ;}

²⁾

1) только а и в; 2) только б и в ; 3) только б ; 4) ни одна; 5) все.

29

на оси орндаионсаит оррадвниына:т равны:

_{1) b=4, k1=)3;b=4, k2=)3b;=-4, k2=) 2b;=-4, 3k)=b2=; 4/3,3k)=b2=/34;/34,)kb==23/3, ;k4=)-1b.=53; , k=5-)1b.5=;-4, k5=) 3b.=-4, k=3.}

5. 5.

Национальный открытКыайноиннисчтКеисаткунотоенРиочсусерисакивонге. нСиауенраквтон-кПернеуитжеенробосуктрирг,ужност показаннпоойканзаарнинсоуйннкае,римсеуенткев,иидм: еет вид:

_{21) 2 ; ;}

^{7. Функция y = e x + 1 отображает множеств1о) (}₍^{x−∞+ 1;0)} _] ^{+н(аyxм+н=1о1)ж2 +есyт2во=:1}

2) 2)

_{1) (− ∞;2] ; 2) [1;2];}

_{3) (0;2]; 4) (1;2]; 5) (− ∞;1) .}

2

_{8. Предел lim} ^3x

^{− 3x − 18} _равен:

^x→−2

_{2 x} ² _{− 8}

₁₎ ⁵ _{; 2)} ⁵ _{; 3)} ^{1 5} _{; 4) −} ^{1 5} _{; 5)} ¹₌ ⁵ _.

4 8 4 8 8

^{9. Уравнение касательной к графику функции} _{y =} ¹

^{x 2 + 1}

в точке (-1; 0.5) имеет вид:

1) x+2y-2=0; 2) x+2y=0; 3) x-2y-2=0; 4) x-2y+2=0; 5) x-2y=0.

10. График какой функции на всем отрезке

_{x +}

1) x+2y-2=0; 2) x+2y=0; 3) x-2y-2=0;

4) x-2y+2=0; 5) x-2y=0.

^{10. График какой функции на всем отрезке [a, b] одновременно удовлетворяет трем}

^{условиям: y < 0 ; y ′ < 0 ; y ′′ > 0 ?}

Варианты ответов:

Варианты ответов: