Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный педагогический университет им. М.П. Драгоманова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

sfme2009_8

.pdf

Скачиваний:

Добавлен:

28.02.2016

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

Кукуруза А.О.

Ланцюгова функція

Друга функція задана з використанням ланцюгового зображення числа.

Як відомо дріб виду: c = a0 +			1			називають ланцюговим, що
Як відомо дріб виду: c = a0 +			1			називають ланцюговим, що
	a +		1

		a	+		1
1		a	+		1
1

2				a	+L
			3
скорочено записують так: с = [a0, a1, a2, a3 ,…].
Розглянемо ланцюговий дріб [α0, α1, α2 , …,					αn ,… ]. Якщо αn {α1;α2} =

А, де n N і 0 < α1 < α2 , то ланцюговий дріб називається двомісним, а множина А — його алфавітом.

Для задання функції було використано двомісні ланцюгові дроби з

алфавітом А =

;1 і вона задовольняє таким умовам:

Функція визначена на відрізку [0;1].

Її аргумент х [0;1] представимо двійковим дробом.

Відповідні значення функції у = f(x)=

...β

, де вk

;1 ,—

символічне

зображення числа за допомогою двомісного ланцюгового дробу.

Функція набуває значень у

;1 , оскільки мінімальне значення

ланцюгового дробу з А=

;1 дорівнює

а максимальне дорівнює 1.

Відповідність між αk і βk встановлено таким чином, що

βk

, якщо αk = 0 і βk = 1 , якщо αk = 1.

Наближений графік після четвертого кроку побудови зображено на мал. 2.

50	Математика

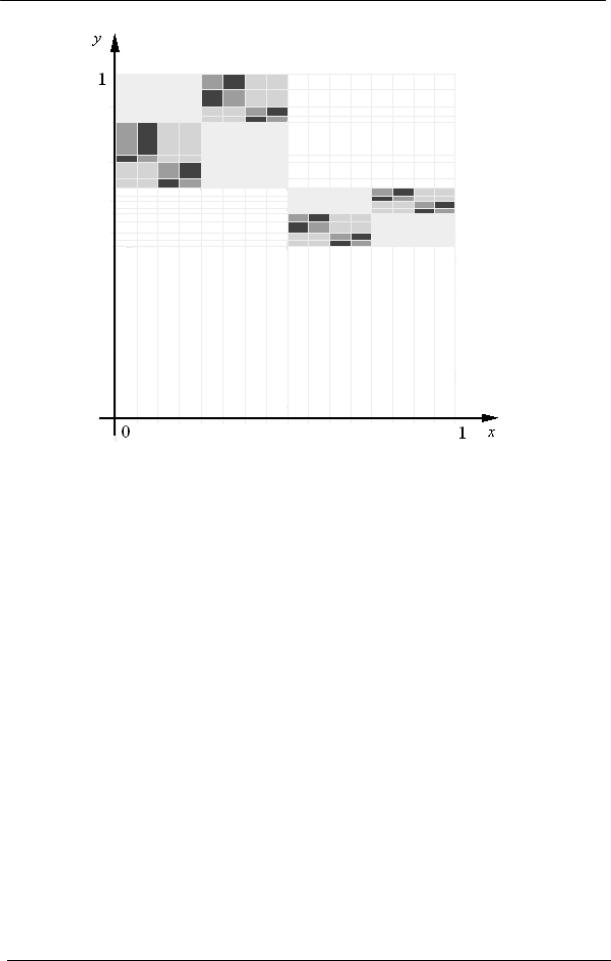
ВИКОРИСТАННЯ МЕДІАНТНИХ І ЛАНЦЮГОВИХ ДРОБІВ ДЛЯ ЗАДАННЯ ФРАКТАЛЬНИХ ФУНКЦІЙ

Мал. 2

З побудови графіка стає зрозуміло, що функція хоч і визначена в кожній точці, але також в кожній точці є розривною, в чому і проявляється складність її локальної структури.

Висновки

На сьогоднішній день людство зіткнулося з такими процесами і явищами, вивчити і описати які за допомогою “ традиційних” функцій, заданих за допомогою відомих способів, неможливо внаслідок їх складної локальної структури. Отже, стає очевидною потреба в створенні нових функціональних залежностей та способів їх задання саме для вивчення і опису таких процесів і явищ. Дещо вирішити цю проблему дозволяє використання двоалфавітних систем числення і символьного способу задання функцій. Задані функції є прикладом застосування такого способу для задання фрактальних функцій, крім того ці приклади розширюють класи функцій зі складною локальною структурою.

Студентські фізико-математичні етюди, 2009, № 8

Кукуруза А.О.

Література

1.Кравченко В.Ф., Масюк В.М. Новый класс фрактальных функций в задачах аналитического синтеза антенн. Кн. 3. — М.: ИПРЖР, 2002. — 72 с.

2.Працьовитий М.В. Фрактальні властивості однієї неперервної ніде не диференційовної функції // Наукові записки НПУ імені М.П.Драгоманова. Фізико-математичні науки. — № З, 2002.-С. 327-338.

3.Працьовитий М.В.,Чумак М.Є. Фрактальність і канторовість розподілу однієї комплекснозначної випадкової величини типу Джессена-Вінтнера // Наукові записки НПУ імені М.П.Драгоманова. Фізико-математичні науки.— Київ: НПУ імені М.П.Драгоманова, 1999.— 1.— С.244-250.

4.Турбин А.Ф., Працевитый Н.В. Фрактальные множества, функций, распреде-ления.

— Киев: Наук, думка, 1992. — 208 с.

5.Працьовита І.М. Модифікації класичних фракталів за допомогою складного

золотого поділу відрізка // У світі математики. — 2002. — Том 8. — Вип. 4. — С. 16-27. 6. Дмитренко С.О. М-представлення чисел і випадкові величини з ним пов'язані // Студентські фізико-математичні етюди. К.: НПУ імені М.П.Драгоманова, 1999.№1.— С.

17-25.

7. Дмитренко С.О. Наближення дійсних чисел за допомогою медіантного представлення // Студентські фізико-математичні етюди. К.: НПУ імені М.П.Драгоманова, 2000.№1.— С. 26-29.

52	Математика

О. П. Вишняк,

студент Фізико-математичного інституту НПУ імені М.П.Драгоманова Науковий керівник: старший викладач Василенко Н. М.

ПРО ПОСЛІДОВНІСТЬ ТРІБОНАЧЧІ ТА ДЕЯКІ ЇЇ ВЛАСТИВОСТІ

У роботі розглянуто послідовність трібоначчі (3-крокову послідовність Фібоначчі) та досліджено деякі її властивості. Доведено, що множина всіх послідовностей трібоначчі утворює тривимірний векторний простір, базис якого є ортонормованим.

Вступ

Числова послідовність трібоначчі є одним з багаточисельних узагальнень класичної послідовності Фібоначчі і належить до, так званих, п-крокових послідовностей Фібоначчі [6, 10].

О з н а ч е н н я 1 . п-кроковою послідовністю Фібоначчі називається

числова послідовність, загальний член якої задовольняє наступним рекурентним співвідношенням

sk = sk −1 + sk −2 + ... + sk −n , k > n ,	s1, s2 ,..., sn R .	(1)
О з н а ч е н н я 2 . 3-крокова послідовність	Фібоначчі називається

послідовністю трібоначчі, а її загальний член задовольняє наступним рекурентним співвідношення

tn = tn−1 + tn−2 + tn−3 , n > 3 , t1 , t2 , t3 R .	(2)
Термін „ послідовність трібоначчі” був введений 14-річним	студентом
Марком Фейнбергом (M. Feinberg) [5] у 1963 році для випадку, коли
t1 = t2 = 1, t3 = 2 .	(3)

О з н а ч е н н я 3 . Послідовність трібоначчі, яка задовольняє початковим умовам (3), будемо називати класичною, по аналогії з послідовністю Фібоначчі.

Послідовність трібоначчі, на сьогодні, достатньо вивчена. Про це говорить наявність ряду наукових публікацій з даної тематики [1-10]. У зв’язку з тим, що значна частина з них має обмежений доступ, наприклад, роботи [1, 5, 7 – 9], ми не маємо повного уявлення про властивості цієї послідовності і будемо досліджувати їх самостійно.

Студентські фізико-математичні етюди, 2009, № 8

Вишняк О.П.

Для вивчення послідовності трібоначчі ми будемо використовувати ті методи та прийоми, що й для класичної послідовності Фібоначчі. Детальніше з ними можна ознайомитись в [11].

1. Генератриса числової послідовності трібоначчі

Метод генератрис –– найбільш потужний метод комбінаторики, який дозволяє вивчати числові послідовності засобами математичного аналізу.

Означення		4 [13]. Генератрисою						числової послідовності (an )∞n=0
							∞
називається сума степеневого ряду A(t) = ∑an xn .
						n=0
Має місце твердження.
Теорема 1 (єдиності для генератриси) [13]. Якщо при деякому
додатному с функцію			f (x) можна представити у вигляді степеневого ряду
∞			(−c;c), то коефіцієнти ап визначаються однозначно.
∑ an xn на інтервалі			(−c;c), то коефіцієнти ап визначаються однозначно.
n=0
Доведення теореми 1 ґрунтується на властивостях степеневих рядів.
Знайдемо вираз T (x) генератриси числової послідовності трібоначчі. З
означення 1 слідує, що
∞						∞		∞	∞
T (x)= ∑tn xn−1			= t1 + t2 x + t3 x2 + ∑tn−1xn−1 + ∑tn−2 xn−1 + ∑tn−3 xn−1 . (4)
n=1						n=4		n=4	n=4
Враховуючи, що
			∞		(T (x)			−t1 −t2 x)x ,
			∑tn−1xn−1	=	(T (x)			−t1 −t2 x)x ,
			n=4
			∞	−1	= (T (x) −t1 )x2 ,
			∑tn−2 xn	−1	= (T (x) −t1 )x2 ,
			n=4
			∞
			∑tn−3 xn−1 = T (x)x3 ,
			n=4
рівність (4) може бути переписана у вигляді
T (x) = t + t	2	x + t x2 + (T (x) −t −t					2	x)x + (T (x) −t )x2	+T (x)x3
1	2		3		1		2	1

З останньої рівності знаходимо вираз Т(x) генератриси числової послідовності (2):

54	Математика

ПРО ПОСЛІДОВНІСТЬ ТРІБОНАЧЧІ ТА ДЕЯКІ ЇЇ ВЛАСТИВОСТІ

	(t + t	2	−t	3	)x2 + (t −t	2	)x −t
T (x) =	1	2		3	1	2	1	.
T (x) =			x3 + x2 + x −1					.
			x3 + x2 + x −1

2.Властивості числової послідовності трібоначчі

Уданому розділі ми розглянемо найпростіші властивості послідовності трібоначчі, доведення яких ґрунтується на означенні 2.

Властивість 1. Сума п перших членів послідовності трібоначчі обчислюється за формулою

t1 + t2 +... + tn = 1 (tn+3 − tn+1 + t1 − t3 ).

↓ Нехай (tn) –– числова послідовність трібоначчі. Тоді виконуються рівності

t1 = t4 − t2 − t3 , t2 = t5 − t3 −t4 , t3 = t6 − t4 − t5 ,

. .

tn−2 = tn+1 −tn−1 − tn ,

tn−1 = tn+2 − tn − tn+1,

tn = tn+3 − tn+1 − tn+2 .

Додавши почленно записані вище рівності, одержимо

t1 + t2 +... + tn = −t2 −t3 −... −tn + tn+3 −tn+1 −t3 ,

що рівносильно

t1 + t2 +... + tn = (−t1 −t2 −t3 −... −tn ) + tn+3 −tn+1 + t1 −t3 .

Звідки

+ t

+... + t

−t

+ t −t

). ↑

n+3

n+1

Властивість 2.

Сума членів

послідовності

трібоначчі

з непарними

номерами обчислюється за формулою

t + t

+... + t

+ t

−t

2n−1

2n+1

↓ Нехай (tn) ––

числова

послідовність

трібоначчі, тоді

виконуються

рівності

Студентські фізико-математичні етюди, 2009, № 8

Вишняк О.П.

t1 R, t3 R,

t5 = t6 −t3 − t4 , t7 = t8 −t5 −t6 ,

t9 = t10 − t7 − t8 ,

. . . ,

t2n−3 = t2n−2 −t2n−5 t2n−1 = t2n − t2n−3 −

− t2n−4 ,

t2n−2 .

Додавши почленно записані вище рівності, одержимо

t1 + t3 +... + t2n−1 = −t3 −t5 −... −t2n−3 + t2n −t4 ,

що рівносильно

t1 + t3 +... + t2n−1 = (−t1 −t3 −... −t2n−3 −t2n−1 ) + t2n+1 + t2n + t1 −t4 .

З останньої рівності маємо

2 (t1 + t3 +... + t2n−1 )= t2n+1 + t2n + t1 − t4

або

t1 + t3 +... + t2n−1 = 1 (t2n+1 + t2n − t2 − t3 ). ↑

Властивість 3. Сума членів послідовності трібоначчі з парними номерами обчислюється за формулою

t		+ t		+... + t		=	1	(t		− t		+ t + t		).
	2		4		2n				2n+2		2n+2		2
						2						1

↓ Нехай (tn) –– числова послідовність трібоначчі. Тоді має місце рівність

t2 + t4 +... + t2n = (t1 + t2 +K + t2n−1 + t2n )− (t1 + t3 +K + t2n−1 ).

Враховуючи властивості 2 та 3, остання рівність може бути переписана у вигляді

t2 + t4 +... + t2n = 12 (t2n+3 − t2n+1 + t1 − t3 )− 12 (t2n+1 + t2n − t2 − t3 ) =

=12 (t2n+2 + t2n+1 + t2n − 2t2n+1 − t2n + t1 + t2 )=

=12 (t2n+2 −t2n+1 + t1 + t2 ). ↑

56	Математика

ПРО ПОСЛІДОВНІСТЬ ТРІБОНАЧЧІ ТА ДЕЯКІ ЇЇ ВЛАСТИВОСТІ

A =

(T ) ––

Властивість 4

[4].

Нехай

––

трібоматриця,

класична послідовність трібоначчі. Тоді для довільного

n N

має місце

рівність

1 1

0 n

n−1

= T +T

(5)

n−1

n−2

n−

n−3

n−1

n−2

↓ Для доведення властивості 4 використаємо метод математичної індукції.

Перевіримо виконання рівності (5) для п = 1. Матимемо

1 1

1 0

= T +T T +T

−1

−2

−1

де T1 =T2 =1, T3 = 2 , T0 =T3 −T2 −T1 = 0 , T−1 =T2 − T1 −T0 = 0 ,

T−2 =T1 −T0 −T−1 =1. Отже, рівність (5) має місце.

Припустимо, що рівність (5) виконується для n = k ,

1 1

0 k

k +1

k −1

−1 + Tk −2

1 0

Tk + Tk −1

Tk −2 + Tk −3 .

−1

k −2

Покажемо її виконання для n = k +1. Матимемо

+ 1

Ak + 1 = Ak

k -1

× A = T + T

+ T

- 2

+ T

- 3

1 0 1

-1 k -1

-1

k - 2

(T + T

Tk +1

+ Tk + Tk −1

)

Tk +1

+ T

)+ (T

+ T

−2

+ T

T + T

−1

+ T

k −1

k −2

k −1

k −3

k −1

k −

Tk + Tk

−1 + Tk −2

Tk −1

Tk +2

Tk +1

Tk +Tk −1

Tk +1 +Tk

Tk −1 +Tk −2 .

k −1

Отже, за принципом математичної індукції рівність (5) має місце для довільного натурального п. ↑

Студентські фізико-математичні етюди, 2009, № 8

Вишняк О.П.

3. Простір послідовностей трібоначчі

Позначимо через

R	= (tn ):t1,t2 ,t3 R, tn = tn−1 + tn−2 +tn−3 , n > 3}
T ={t

— множину всіх послідовностей трібоначчі (множину нескінченних векторів, координати яких є відповідними членами послідовностей трібоначчі). Очевидно, що ця множина є непорожньою, оскільки із співвідношення (2) слідує, що існує нескінченна кількість послідовностей трібоначчі.

Введемо на	цій		множині операції додавання та множення на скаляр.
Візьмемо довільні елементи				R		Î T і поставимо їм у відповідність елемент c
Візьмемо довільні елементи				a, b		Î T і поставимо їм у відповідність елемент c
за законом
		R	R	+ b = (an )+ (bn )= (an + bn ),
		c	= a	+ b = (an )+ (bn )= (an + bn ),
який назвемо сумою a та b . Оскільки
an + bn = an−1 + an−2 + an−3 + bn−1 + bn−2 + bn−3 =
= (a		n−1	+ b		) + (a		n−2	+ b	) + (a	+ b	) ,
		n−1	n−1				n−2	n−2	n−3	n−3
R
то c T .
Візьмемо довільні елементи				R		і λ R . Поставимо їм у відповідність
Візьмемо довільні елементи				a T		і λ R . Поставимо їм у відповідність
елемент
							R	= (λan ),
					d = λ × a			= (λan ),
який назвемо добутком елемента a на скаляр λ . Оскільки
λ an = λ(an−1 + an−2 + an−3 ) = λ an−1 + λ an−2 + λan−3 ,
то d T
Т е о р е м а	2. Множина					всіх		послідовностей трібоначчі разом з

введеними на ній операціями додавання і множення на скаляр λ є лінійним (векторним) простором.

↓ Покажемо,			що	виконуються всі аксіоми лінійного (векторного)
простору.
R	T ,	R		R	оскільки
1) a,b	T ,	a + b = b + a ,			оскільки
R					R
a + b = (a1 + b1; a2 + b2; ... ak + bk ;...)= (b1 + a1; b2 + a2; ... bk + ak ; ...)= b + a. 2)
R R	T ,	R	R	R	R
a, b, c	T ,	(a + b) + c		= a	+(b + c) , оскільки
R	R	((a1 + b1) + c1; (a2 + b2 ) + c2;...(ak + bk ) + ck ;...)=
(a + b )+ c =		((a1 + b1) + c1; (a2 + b2 ) + c2;...(ak + bk ) + ck ;...)=

58	Математика

ПРО ПОСЛІДОВНІСТЬ ТРІБОНАЧЧІ ТА ДЕЯКІ ЇЇ ВЛАСТИВОСТІ

							R	R
= (a1 + (b1 + c1); a2 + (b2 + c2 );...; ak + (bk + ck ); ...)= a								+ (b + c ).
	3)	R	T ,	R	+ 0	R	= (0; 0; ...0; ...).
	3)	a	T ,	0 T : a	+ 0	= a , де 0	= (0; 0; ...0; ...).
	Справді
		R		= (a1 + 0; a2 + 0; ... ak +				R
		a	+ 0	= (a1 + 0; a2 + 0; ... ak +			0; ...)= (a1; a2; ... ak ; ...)= a .
	4)	R	T	R	R	R
	4)	a	T	-a T : a +		(-a) = 0 , оскільки
R		R
a	+ (−a) = (a1 + (−a1); a2 + (−a2 ); ... ak + (−ak ); ...)= (0; 0; ... 0; ...) = 0 .
	5)	R	ÎT		R	R
	5)	" a	ÎT	$ 1Î R : 1× a = a , оскільки
			R					R
	6)		1× a	= (1× a1; 1× a2; ...1× ak ; ...) = (a1; a2; ... ak ; ... ) = a .
	6)	" a ÎT		$ λ, μ Î R : λ(μ a) = (λμ)a , оскільки
		R				R	R

		R	R	R	R	=
		λ(μ a) = (λ(μ a1); λ(μ a2 ); ...			λ(μ ak ); ...)	=
		= ((λμ)a1; (λμ)a2; ... (λμ)ak			; ...) = (λμ)a.
					R
R	ÎT	$ λ, μ Î R :	R	R	R
7) " a	ÎT	$ λ, μ Î R :	(λ + μ)a	= λ a + μ a , оскільки

R			=
(λ + μ)a = ((λ + μ)a1; (λ + μ)a2; ... (λ + μ)ak ; ...)
= (λ a1 + μ a1; λ a2 + μ a2; ... λ ak + μ ak ; ...) =
= (λ a1; λa2; ... λ ak ; ...) +		R
		(μ a1; μ a2; ... μ ak ; ...) = λ a + μ
R	R	R
8) a, b T , λ R :	λ(a + b ) = λ a + λ b , оскільки
R	+ b1);λ(a2 + b2 );...λ(ak + bk );...) =
λ(a + b ) = (λ(a1			R
= (λ a1 + λ b1;λ a2 + λ		R
		b2;...λ ak + λ bk ;...) = λ a +	λ b.

Отже множина всіх послідовностей трібоначчі утворює лінійний простір. Далі цю множину будемо позначати (T ,+,λ(×)). ↑

R R R	T ,
Т е о р е м а 3. Впорядкована система векторів b1, b2 , b3 , де bi

i =1, 2,3, b1 = (0;0;1;...) , b2 = (0;1;0;...) , b3 = (1;0;0;...) є базисом векторного простору (T ,+,λ(×)).

↓ Покажемо, що система векторів b1, b2 , b3 є лінійно незалежною, тобто,

що з рівності α1b1 +α2b2 +α3b3 = 0 слідує α1 = α2 = α3 = 0 . Припустимо що α1 ¹ 0 , тоді

Студентські фізико-математичні етюди, 2009, № 8

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.02.2016131.58 Кб17Seminari_Istoriya_Ukrayini_1_kurs.doc
#
28.02.201646 Кб13Seminari_z_filosofiyi_-_plani_33_1_sem.docx
#
24.11.201983.18 Кб2seminar_DID_11_vstup_do_fakhu.docx
#
28.02.201636.62 Кб93Seminar__9.docx
#
21.08.2019712.19 Кб4Senin.doc
#
28.02.20161.92 Mб19sfme2009_8.pdf
#
28.02.2016134.97 Кб282ShPORA.docx
#
24.12.2019484.2 Кб0Shpori_ekzamen_TOM.docx
#
28.02.2016277.74 Кб22shpori_ist_ukr_kult (1)норм.docx
#
28.02.2016738.61 Кб27shpori_na_ukr_movu.pdf
#
26.12.2019376.32 Кб0shpori_op.doc