sfme2009_8

Савченко І.О., Філєр З.Ю.

ЛІТЕРАТУРА

1.Воробьев Н.Н. Теория рядов: Учеб. пособие для втузов. М.: Наука, 1986. – 408 с.

2.Дороговцев А.Я. Ряды. К.: Вища школа, 1978, 112 с.

3.Рыжик И. М., Градштейн И. С. – Таблицы интегралов, сумм, рядов и произведений. Изд. 3, пер. М.-Л.: ГИТ-ТЛ, 1951. – с. 464.

4.Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. Продолжение курса. – М.: МГУ, 1987. – 358 с.

5.Савченко І.О., Філєр З.Ю. Використання сталої Ейлера для обчислення сум // Матеріали науково-практичної конференції, присвяченої 80-річчю фізикоматематичного факультету. 26.11.2010 р. – Кіровоград: Лисенко С.В., 2010. – С. 20-22.

6.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. В 3 т. Т. II / Пред. и прим. А.А. Флоринского. – 8- е изд. – М.: ФИЗМАТЛИТ, 2003. – 864 с.

7.Эйлера постоянная/в кн. Математический энциклопедический словарь. – М.: Сов.

энц., 1988. – с. 641.

Карпенко О.В.

1. Лінійність простору арифметичних прогресій

Нехай A – множина всіх арифметичних прогресій, включаючи

(0,0,...,0,...) , тобто

An = {(an ) : an R, an+1 −an = const}.

Введемо лінійні операції на множині A за правилом

(a1 , a2 ,..., an ,...) + (b1 , b2 ,...bn ,...) = (a1 + b1 , a2 + b2 ,..., an + bn ,...) λ(a1 , a2 ,..., an ,...) = (λa1 , λa2 ,..., λan ,...) ,

де λ – довільне дійсне число.

Очевидно, що замкненість цих операцій має місце. Легко бачити, що пара ( А, +) є адитивною комутативною групою, нейтральним елементом якої є тривіальна арифметична прогресія (0,0,...,0,...) .

Операція множення арифметичної прогресії на скаляр має властивості:

1.λ(μ(an )) = (λμ)(an ) ,

2.(λ + μ)(an ) = λ(an ) + μ(an ) ,

3.λ[(an ) + (bn )] = λ(an ) + λ(bn ) ,

4.1(an ) = (an ) (an ) A ,

перша з яких виражає властивість асоціативності відносно скалярного множника, друга – дистрибутивність відносно додавання скалярів, третя – дистрибутивність відносно додавання прогресій.

Підсумовуючи сказане, отримаємо наступне твердження.

Теорема 1. Множина всіх арифметичних прогресій разом з операціями додавання та множення прогресій на скаляр утворює векторний (лінійний) простір, тобто алгебраїчна структура ( А,+,λ(×)) є векторним простором.

Зауваження. Грубо кажучи, кожна арифметична прогресія є “ вектором”, тобто арифметична прогресія є однією з моделей вектора. Це дає підставу елементи множини А називати векторами і використовувати відповідну символіку

(an ) = (a1 , a2 ,..., an ,...) = a A.

Поняття лінійної залежності та лінійної незалежності системи векторів, добре відомі з курсів лінійної алгебри та аналітичної геометрії, тепер можуть бути використані для елементів простору арифметичних послідовностей. На їх основі вводяться поняття базису простору та його розмірності.

ЛІНІЙНИЙ ПРОСТІР АРИФМЕТИЧНИХ ПРОГРЕСІЙ

З’ясуємо, які прогресії утворюють базис даного векторного простору і яку розмірність він має?

2. Скінченновимірність простору арифметичних прогресій

Теорема 2. Впорядкована пара векторів

e1 = (1,0,−1,−2,...) , e2 = (0,1,2,3,...)

a = a1e1 + a2 e2 , то (e1 , e2 ) – базис.

Теорема доведена.

Наслідок 1. Простір арифметичних прогресій має розмірність два, тобто є двовимірним простором.

Наслідок 2. Вектор а = (аn ) A в базисі < e1 , e2 > має координати

(a1 , a2 ) .

Теорема 3. Вектори a = (an ) і b = (bn ) є лінійно залежними тоді і тільки тоді, коли

b1 = b2 . a1 a2

Доведення. Справді, a і b є лінійно залежними згідно з основною

теоремою про лінійну залежність тоді і тільки тоді коли = λR тобто

, , b a ,

b1 = λa1 ,= λb2 a2 ,

а, отже,

λ= b1 = b2 . a1 a2

Теорему 3 доведено.

Карпенко О.В.

Наслідок 3. Вектори а = (аn ) A , b = (bn ) A є лінійно залежними тоді і тільки тоді, коли

b2 = a2 або a1b2 − а2b1 = 0 . b1 a1

3. Оператор зсуву

Означимо лінійний оператор σ в просторі А рівністю a′ = σ (a) = (a2 , a3 ,.., an ,...) ,

де a = (a2 , a3, ..., an ,...) .

Лема 1. Вектори a і a′ = σ (a) є лінійно залежними тоді і тільки тоді, коли a2 − a1 = d = 0 .

Доведення. Згідно з теоремою 3 a і a′ = σ (a) є лінійно залежними тоді і тільки тоді, коли

a2 = a3 Û a22 = a3a1 (1),

a1 a2 але a3 = a2 + d , a1 = a2 − d .

Тому рівність (1) переписуємо у вигляді

a22 = (a2 + d )(a2 - d ) ,

що рівносильно d = 0 . Лему доведено.

4. Евклідовість простору арифметичних прогресій

Введемо в просторі арифметичних прогресій операцію скалярного множення векторів. З цією метою зафіксуємо базис < e1 , e2 >.

ЛІНІЙНИЙ ПРОСТІР АРИФМЕТИЧНИХ ПРОГРЕСІЙ

ортонормованим, оскільки вектори, що до нього входять є одиничними і взаємно перпендикулярними.

5. Нормованість простору арифметичних прогресій

Поняття скалярного добутку векторів дозволяє ввести в просторі А норму елемента а наступною рівністю

6. Метричний простір арифметичних послідовностей

Наявність норми у просторі А дозволяє ввести поняття відстані (метрику) між точками цього простору. Метрику ρ в цьому просторі задає функція двох змінних, визначена рівністю:

Перетворення простору арифметичних прогресій в евклідів нормований повний метричний простір дозволяє задавати в ньому різні геометричні об’єкти, розглядати і досліджувати фрактали.

Карпенко О.В.

9.Василенко Н.М., Працьовитий М.В. Простір послідовностей Фібоначчі // Науковий часопис НПУ імені М.П. Драгоманова. Серія 1. Фізикоматематичні науки. –– № 9. –– К.: НПУ імені М.П. Драгоманова, 2008.

Кукуруза А.О.

Результатом дослідження можливих використань двійкової системи числення, двомісних ланцюгових дробів та медіантного представлення чисел для задання фрактальних функцій, стали дві нові такі функції, які дещо розширюють класи функцій зі складною локальною структурою.

Обидві функції задано з використанням символьного способу.

Лінійно-медіантна функція

Для задання першої функції, яку названо лінійно-медіантною, використано медіантне зображення числа. Таке зображення полягає у визначенні числа системою вкладених відрізків. Кожен такий відрізок отримується за допомогою подрібнюючих розбиттів спочатку відрізка [0;1], а потім і отриманих відрізків медіантою його кінців на два відрізки вищого рангу.

Так якщо кінці відрізка [0;1] представити у вигляді 0 = 0 і 1 = 1 , то

1 1

медіантою є дріб 1 , який розбиває відрізок [0;1] на два відрізки першого рангу:

2

У свою чергу кожен з цих відрізків медіантами кінців розбивається на відрізки 2-го рангу:

Отже для кожної точки з відрізка [0;1] існує відрізок 1-го рангу, відрізок 2- го рангу і т.д., що містять точку х. За аксіомою Кантора ця точка єдина для послідовності вкладених відрізків

Dα1 É Dα1α2 É Dα1α2 α3 É L É Dα1α2 Lαk L .

Таким чином, кожне число х з відрізка [0;1] має своє М-представлення, елементи якого визначаються наступним чином

Лінійно-медіантна функція у = f(x) задовольняє наступні умови: 1)Функція визначена на відрізку [0;1].

ВИКОРИСТАННЯ МЕДІАНТНИХ І ЛАНЦЮГОВИХ ДРОБІВ ДЛЯ ЗАДАННЯ ФРАКТАЛЬНИХ ФУНКЦІЙ

відрізка [0;1] за допомогою медіантного представлення. 4) Для відповідних х і у значення α1, α2, α3, ..., αk ті самі.

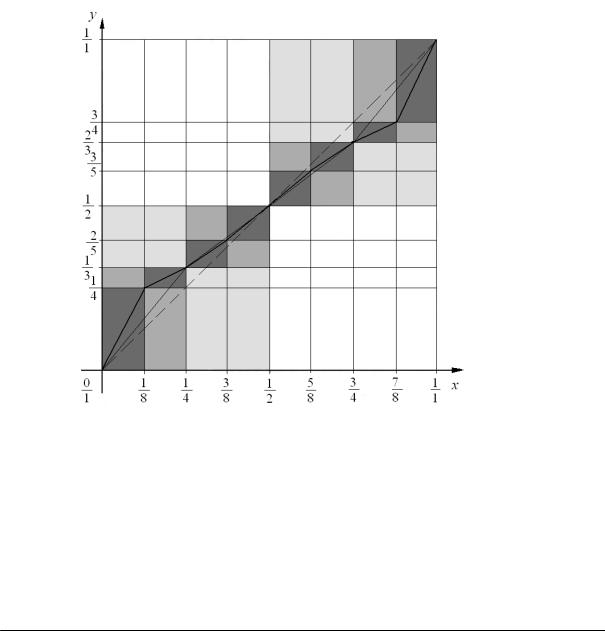
Наближений графік після третього кроку побудови (заштриховані області

—це області в яких містяться точки графіка) зображено на мал.1.

Складність локальної структури полягає в тому що дана функція хоч і зростає на всій області визначення, але разом з тим існує безліч точок в яких похідна даної функції дорівнює 0.

Мал. 1