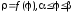- •Тема: Границя функції неперервного аргументу.
- •Диференціальне числення функції однієї змінної. Тема: Похідна функції
- •Тема: Обчислення похідної функції
- •Тема: Похідна складеної функції Теоретичні питання
- •Тема: Диференціювання неявно та параметрично заданих функцій.
- •Тема: Диференціал функції
- •Тема: Похідні та диференціали вищих порядків
- •Тема: Теореми про середнє. Правила Лопіталя Основні означення та теореми
- •Інтегральне числення функції однієї змінної Тема: Основні методи інтегрування
- •Властивості невизначеного інтеграла
- •Таблиця основних інтегралів
- •Основні методи інтегрування
- •Тема: Інтегрування раціональних дробів
- •Інтеграли від елементарних дробів
- •Тема: Інтегрування ірраціональних виразів. Основні означення та теореми
- •Тема: Інтегрування тригонометричних функцій.
- •Інтегралів на збіжність.
- •Ознаки порівняння
- •Числові ряди
- •1.1. Знакододатні ряди
- •Необхідна умова збіжності числового ряду
- •Достатні умови збіжності знакододатних рядів
- •Зразки розв’язання задач
- •Завдання для самостійної роботи
- •1.2. Знакозмінні ряди
- •Зразки розв’язування задач
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •4.2.Розвинення в ряди Фур’є 2π-періодичних функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Відповіді
Інтеграли від елементарних дробів
|
І.
|
Інтегрується методом безпосереднього інтегрування. |
|
ІІ.
|
Знаходиться за допомогою таблиці інтегралів та формули безпосереднього інтегрування. |
|
ІІІ.
|
Інтеграл
знаходиться підстановкою
|
|
ІV.
|
Підстановкою
|
|
|
Рекурентна формула використовується для обчислення інтеграла, де п – ціле додатне число. |
|
|
Інтеграл від многочлена знаходиться безпосередньо, а інтеграл від правильного раціонального дробу зводиться до інтегралів від елементарних дробів. |
Тема: Інтегрування ірраціональних виразів. Основні означення та теореми
|
|
Інтеграли
такого типу зводиться до інтегралів
від раціональних функцій підстановкою
|
|
де
|
Інтеграл
зводиться до інтеграла від раціональної
функції підстановкою
|
|
|
Зводиться
до інтеграла від раціональної функції
підстановкою
|
Тема: Інтегрування тригонометричних функцій.
|
|
Зводиться
до табличних інтегралів. Якщо добуток
тригонометричних функцій перетворити
в суму за формулами:
|
|
|
Зводиться до інтегралів від раціональних функцій або до табличних .
|
|
|
Інтеграл
даного виду зводиться до інтегралів
від раціональних функцій за допомогою
універсальної тригонометричної
підстановки
|
Тема:Обчислення визначеного інтеграла безпосередньо, заміною змінних та інтегрування частинами.
|
|
Фігура
|
|
|
Інтегральна
сума для функції
|
|
|
Визначеним
інтегралом
функції
|
|
|
Теорема
про середнє значення визначеного
інтеграла.
Якщо функція неперервна на відрізку
| |
|
|
Геометричне
тлумачення теореми про середнє: площа
криволінійної трапеції | |
|
|
Похідна інтеграла із змінною верхньою межею дорівнює значенню підінтегральної функції при цій межі. | |
|
|
Формула
Ньютона – Лейбніца: визначений інтеграл
від функції | |
|
Властивості визначеного інтеграла | ||
|
|
При переставленні меж інтеграла змінюється його знак. | |
|
|
Інтеграл
від деякої функції
| |
|
|
Сталий
множник
| |
|
|
Інтеграл від алгебраїчної суми функцій дорівнює алгебраїчній сумі інтегралів від даних функцій. | |
|
|
Адитивна
властивість визначеного інтеграла;
площа трапеції
| |
|
|
Наслідок
адитивної властивості в разі, якщо | |
|
|
Наслідок
адитивної властивості в разі, якщо | |
|
|
Нерівність
справедлива, якщо
| |
|
|
Нерівність
справедлива, якщо Нерівність
справедлива, якщо функція
| |
|
Методи інтегрування | ||
|
|
Формула
інтегрування частинами,
справедлива у випадку, де функції
| |
|
|
Формула
заміни змінної
за умов, що функція | |
|
Методи наближеного обчислення | |||
|
|
Обчислення визначеного інтеграла за формулою прямокутників. Відрізок
інтегрування
| ||
|
|
Відрізок
інтегрування
| ||
|
|
Формула обчислення визначеного інтеграла, яку називають формулою Сімпсона. Відрізок
інтегрування поділений на парну
кількість рівних частин ( | ||
|
Об’єм тіл обертання | |||
|
|
Об’єм
| ||
|
|
Об’єм
| ||
|
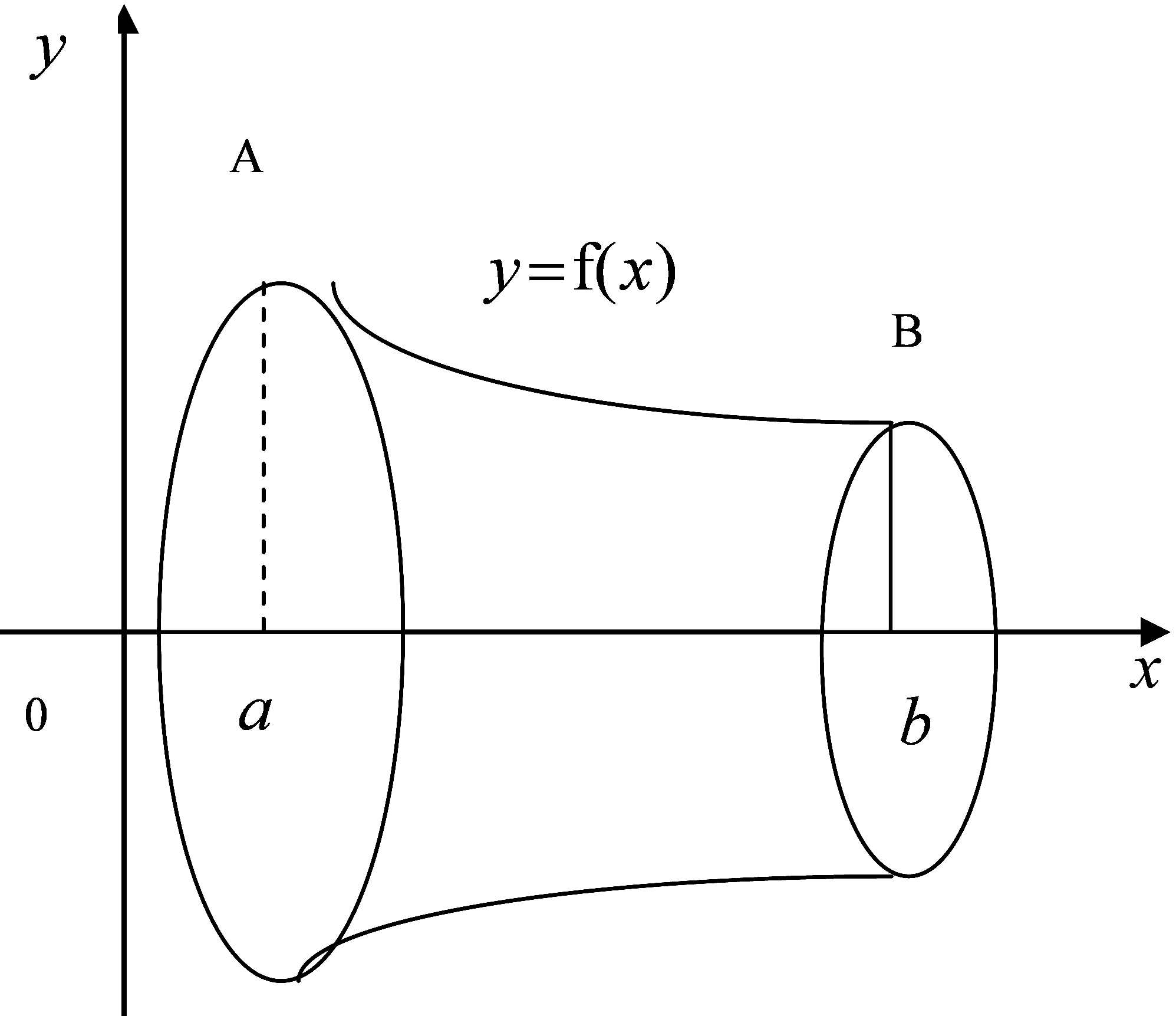
Довжина дуги плоскої кривої | |||
|
|
Під довжиною дуги плоскої кривої розуміють границю, до якої прямує периметр вписаної в неї ламаної лінії, за умови, що кількість ланок ламаної необмежено зростає і довжина найбільшої з ланок прямує до нуля.
Довжина
| ||
|
|
Довжина
дуги кривої, заданої параметрично;
| ||
|
|
Довжина
дуги кривої, заданої в полярних
координатах;
| ||
|
Площа поверхні обертання | |||
|
|
Площа
поверхні, утвореної обертанням навколо
осі
| ||
|
|
Площа
поверхні, утвореної обертанням навколо
осі
| ||
|
|
Площа
поверхні, утвореної обертанням навколо
осі
| ||


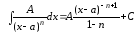
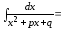
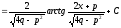 .
.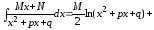
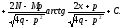
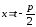 ;
;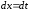 .
.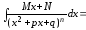
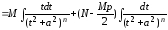
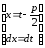 зводиться до двох інтегралів, де
зводиться до двох інтегралів, де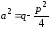 .
Перший інтеграл обчислюється
безпосередньо, а другий рекурентною
формулою.
.
Перший інтеграл обчислюється
безпосередньо, а другий рекурентною
формулою.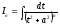
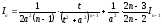
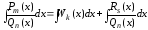
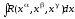 ,
де
,
де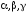 -
дробові раціональні числа ;
-
дробові раціональні числа ;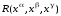 -
раціональна функція від аргументів
-
раціональна функція від аргументів
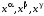 .
.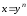 ,
,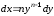 ,
де
,
де -
найменше спільне кратне знаменників
дробів
-
найменше спільне кратне знаменників
дробів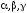 .
Інтеграл зводиться до інтеграла
.
Інтеграл зводиться до інтеграла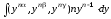 ,
зараз
,
зараз -
цілі числа. Інтеграл звівся до інтеграла
від раціональних функцій.
-
цілі числа. Інтеграл звівся до інтеграла
від раціональних функцій.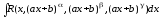 ,
,
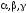 -
дробові раціональні числа.
-
дробові раціональні числа.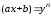 ,
де
,
де -
найменше спільне кратне знаменників
дробів
-
найменше спільне кратне знаменників
дробів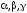 .
.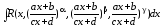 ,
де
,
де
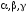 -
дробові раціональні числа.
-
дробові раціональні числа.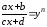 ,
, – найменше
спільне кратне знаменників дробів
– найменше
спільне кратне знаменників дробів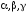


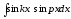
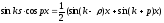
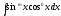
 -
парне, а
-
парне, а -
непарне, то використовують підстановку
-
непарне, то використовують підстановку .
.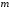 -
непарне, а
-
непарне, а -
парне, то використовують підстановку
-
парне, то використовують підстановку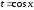 .
.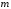 і
і парні, то використовують формули
пониження степеня
парні, то використовують формули
пониження степеня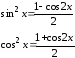
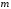 і
і -
непарні, але принаймні одне з них
від’ємне то використовують підстановку
-
непарні, але принаймні одне з них
від’ємне то використовують підстановку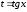 .
.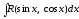 ,
де
,
де 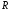 -
раціональна функція.
-
раціональна функція.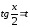 ,
тоді
,
тоді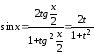 ,
,
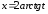 ,
,
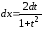 .
.
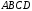 ,
обмежена лініями
,
обмежена лініями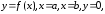 називається криволінійною трапецією.
називається криволінійною трапецією.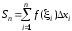
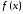 визначеної на відрізку
визначеної на відрізку ,
який розбитий на n відрізків точками
,
який розбитий на n відрізків точками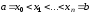 ,
на кожному з яких вибрана довільна
точка
,
на кожному з яких вибрана довільна
точка
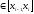 ,
,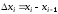 .
.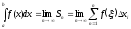
 на відрізку
на відрізку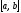 називають границю інтегральної суми,
якщо ця границя існує і не залежить
від способу розбиття відрізка
називають границю інтегральної суми,
якщо ця границя існує і не залежить
від способу розбиття відрізка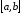 на частини та вибору точок
на частини та вибору точок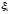
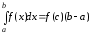
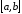 ,
то існує точка
,
то існує точка є
є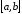 така, що виконується рівність.
така, що виконується рівність.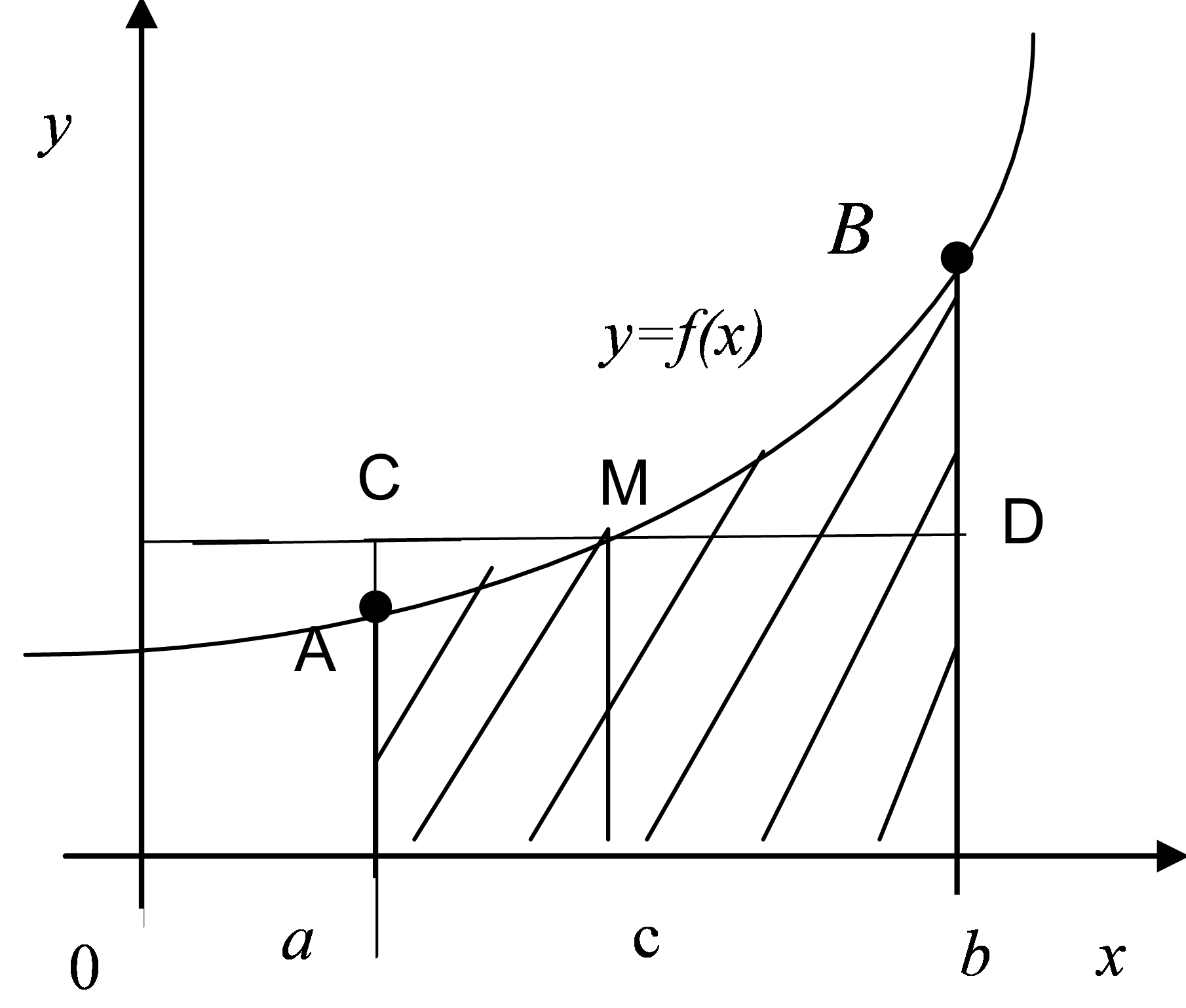
 дорівнює площі прямокутника
дорівнює площі прямокутника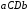 ,
основа якого збігається з основою
трапеції, а висота дорівнює
,
основа якого збігається з основою
трапеції, а висота дорівнює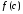

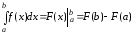
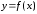 на відрізку
на відрізку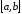 дорівнює приросту первісної функції
дорівнює приросту первісної функції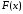 на цьому відрізку.
на цьому відрізку.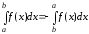
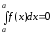
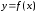 в межах, що дорівнюють одному й тому
ж числу, дорівнює нулю.
в межах, що дорівнюють одному й тому
ж числу, дорівнює нулю.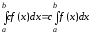
 можна виносити за знак визначеного
інтеграла.
можна виносити за знак визначеного
інтеграла.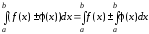

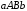 дорівнює сумі площ двох трапецій, на
які вона поділяється прямою
дорівнює сумі площ двох трапецій, на
які вона поділяється прямою .
.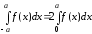
 -
парна функція.
-
парна функція.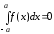
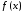 -
непарна функція.
-
непарна функція.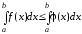
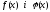 неперервні функції на
неперервні функції на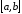 і для кожного
і для кожного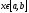 виконується нерівність
виконується нерівність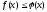 .
.

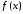 неперервна функція на
неперервна функція на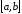 .
.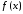 обмежена на
обмежена на і
і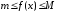
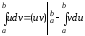
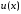 і
і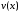 неперервні на
неперервні на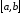 разом із своїми першими похідними.
разом із своїми першими похідними.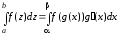
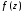 неперервна на
неперервна на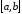 ,
а функція
,
а функція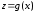 неперервна і має похідну на
неперервна і має похідну на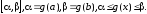 Функцію
Функцію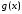 потрібно вибрати так, щоб новий
інтеграл був простішим від початкового.
потрібно вибрати так, щоб новий
інтеграл був простішим від початкового.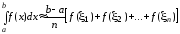
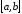 поділений на
поділений на рівних
частин довжиною
рівних
частин довжиною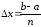 і позначено через
і позначено через середню точку відрізку
середню точку відрізку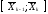 .
.
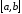 поділений точками ділення
поділений точками ділення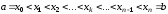 на
на рівних
частин довжиною
рівних
частин довжиною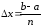 і позначимо значення функції в точках
ділення
і позначимо значення функції в точках
ділення ,
тоді визначений інтеграл можна
обчислити за формулою, яку називають
формулою трапецій.
,
тоді визначений інтеграл можна
обчислити за формулою, яку називають
формулою трапецій.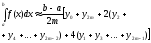
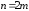 )
і позначимо
)
і позначимо де
де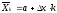 - точки ділення,
- точки ділення,
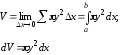
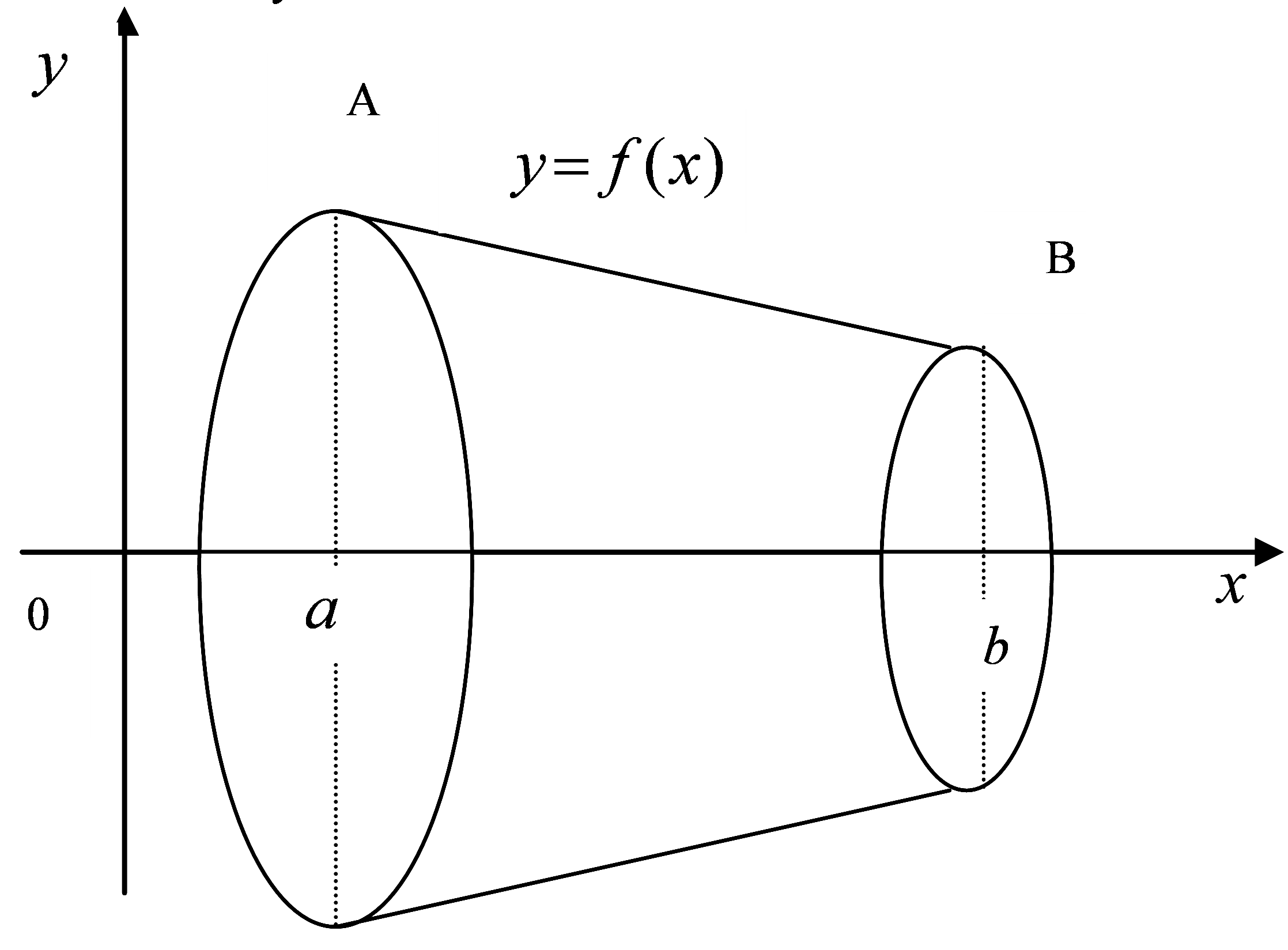
 тіла, утвореного обертанням навколо
осі
тіла, утвореного обертанням навколо
осі криволінійної трапеції
криволінійної трапеції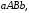 де
де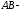 дуга кривої
дуга кривої
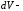 диференціал
змінного об’єму.
диференціал
змінного об’єму. 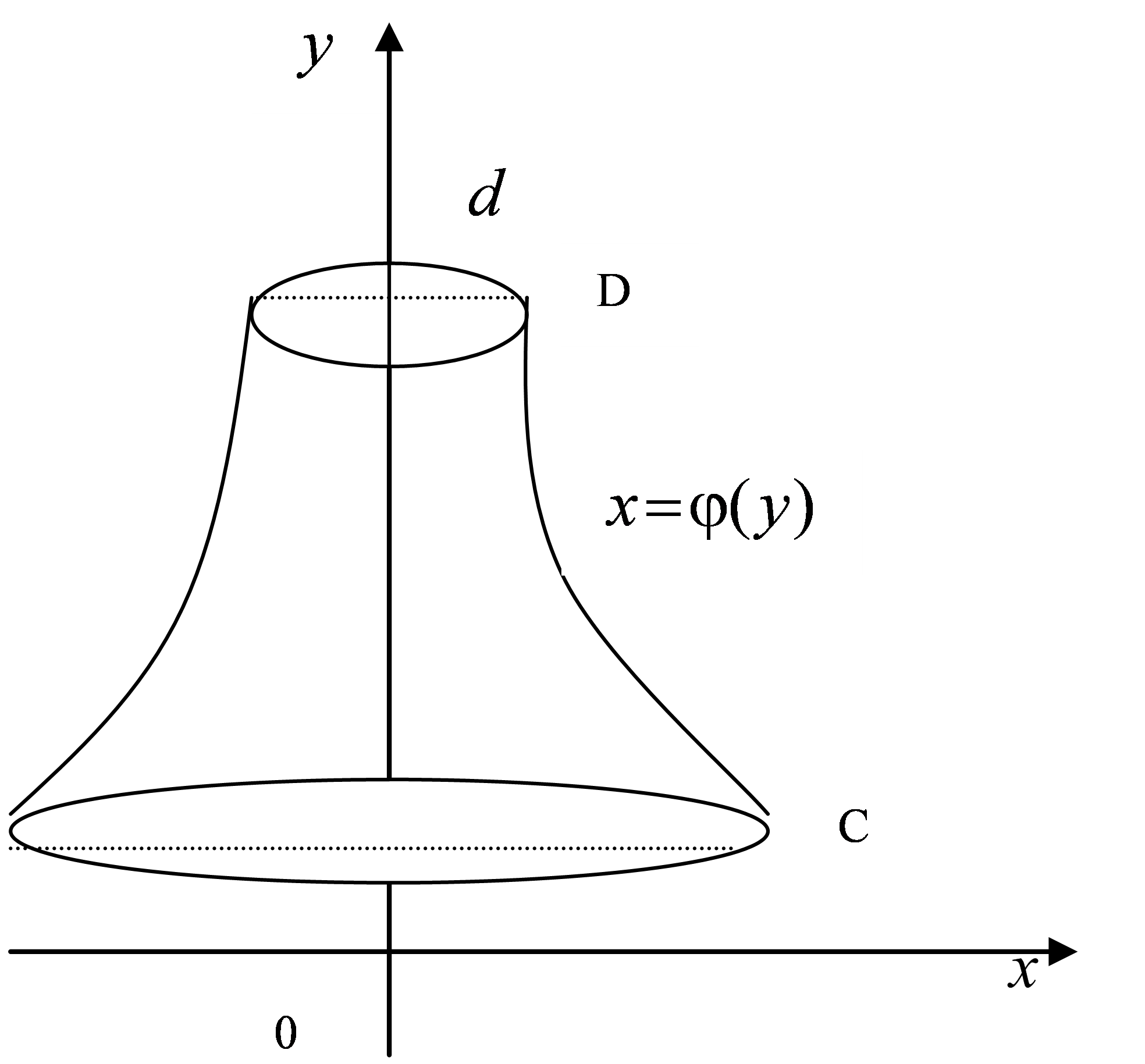
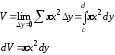
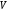 тіла, утвореного обертанням навколо
осі
тіла, утвореного обертанням навколо
осі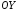 криволінійної трапеції
криволінійної трапеції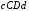 ,
де
,
де -
дуга кривої
-
дуга кривої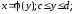
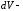 диференціал
змінного об’єму.
диференціал
змінного об’єму.
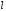 дуги кривої і диференціал
дуги кривої і диференціал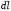 дуги, заданої в прямокутній декартовій
системі координат рівнянням
дуги, заданої в прямокутній декартовій
системі координат рівнянням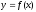
 .
.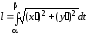

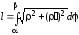

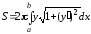
 дуги
дуги кривої
кривої
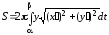
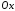 дуги
дуги
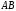 ,
заданої параметричними рівняннями
,
заданої параметричними рівняннями
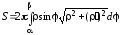
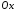 дуги
дуги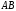 ,
заданої в полярних координатах
,
заданої в полярних координатах