
- •Тема: Границя функції неперервного аргументу.
- •Диференціальне числення функції однієї змінної. Тема: Похідна функції
- •Тема: Обчислення похідної функції
- •Тема: Похідна складеної функції Теоретичні питання
- •Тема: Диференціювання неявно та параметрично заданих функцій.
- •Тема: Диференціал функції
- •Тема: Похідні та диференціали вищих порядків
- •Тема: Теореми про середнє. Правила Лопіталя Основні означення та теореми
- •Інтегральне числення функції однієї змінної Тема: Основні методи інтегрування
- •Властивості невизначеного інтеграла
- •Таблиця основних інтегралів
- •Основні методи інтегрування
- •Тема: Інтегрування раціональних дробів
- •Інтеграли від елементарних дробів
- •Тема: Інтегрування ірраціональних виразів. Основні означення та теореми
- •Тема: Інтегрування тригонометричних функцій.
- •Інтегралів на збіжність.
- •Ознаки порівняння
- •Числові ряди
- •1.1. Знакододатні ряди
- •Необхідна умова збіжності числового ряду
- •Достатні умови збіжності знакододатних рядів
- •Зразки розв’язання задач
- •Завдання для самостійної роботи
- •1.2. Знакозмінні ряди
- •Зразки розв’язування задач
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •4.2.Розвинення в ряди Фур’є 2π-періодичних функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Відповіді
Тема: Числова послідовність та її границя
|
Позначення
числової послідовності: (уп),
або
|
Функція
|
|
Наприклад:1)
2) геометрична прогресія: b1=2, g=0,5 3) послідовність парних чисел
|
Основні способи задання числової послідовності: 1) за допомогою формули п – го члена. 2) рекурентний 3)словесний |
|
Існує
таке число М>0,
що
|
Послідовність (уп) називають обмеженою, якщо значення всіх її членів за модулем не перевищують деякого додатнього числа |
|
Послідовність,
для якої виконується нерівність
уn≥-М=Р,
| |
|
Якщо
для всіх номерів п
виконується нерівність
|
Послідовність (уп) називається неспадною (незростаючою), якщо значення кожного наступного члена послідовності не менше (не більше) значення попереднього її члена |
|
Якщо
значення членів монотонної послідовності
(уп)
для всіх
номерів n
задовольняють строгу нерівність
| |
|
|
Число
А називають
границею
числової послідовності
уп,
якщо для будь-якого ε
> 0 існує
номер члена послідовності N(ε),
що для всіх п
> N(ε)
виконується
нерівність
|
|
|
Якщо числова послідовність уп має скінчену границю, то вона називається збіжною. Якщо числова послідовність границі не має, то вона називається розбіжною. |
|
|
Послідовність уп=f(n) n=1, 2,.. називається нескінченно малою, якщо члени її послідовності із зростанням п, починаючи з деякого номера, прямують до нуля. |
|
Числова
послідовність (уп)
називається нескінченно
малою,
якщо для будь-якого додатного числа
ε
існує натуральне число N(ε)
таке, що для всіх п
> N(ε)
виконується
| |
|
Теорема.
Якщо
| |
|
Теорема. Якщо різниця між уп і числом А є нескінченно малою послідовністю, то А є границею послідовності (уп). | |
|
Теорема. Для того, щоб границя числової послідовності дорівнювала числу А необхідно і достатньо, щоб різниця (уп-А) була нескінченно малою числовою послідовністю. | |
|
(уп-А)=(αп), де (αп) – нескінченно мала послідовність. |
Число А називається границею числової послідовності (уп), якщо різниця між уп і числом А є нескінченно малою послідовністю. |
|
Властивості нескінченно малих послідовностей 1. Алгебраїчна сума скінченого числа нескінченно малих послідовностей є нескінченно мала послідовність 2. Добуток нескінченно малої числової послідовності на обмежену послідовність є нескінченно малою числовою послідовністю. 3. Частка від ділення нескінченно малої величини на функцію, границя якої відмінна від нуля, є величиною нескінченно малою. | |
|
|
Послідовність
(уп)
називається нескінченно
великою,
якщо, яке б не було число М>0,
існує таке число N=N(M),
що для всіх n>N
виконується нерівність
|
|
Теорема.
Якщо (уп)
є нескінченно велика числова
послідовність, то послідовність
Якщо
послідовність
| |
|
Існує єдина границя збіжної числової послідовності
|
Арифметичні властивості збіжних числових послідовностей. Теорема 1. Якщо числова послідовність (хп) має границю, то вона єдина. Теорема 2. Сума або різниця збіжних числових послідовностей є послідовність збіжна. Теорема 3. Якщо послідовності (хп) і (уп) - збіжні, то їх добуток є послідовність збіжна. Наслідок: Сталий множник можна виносити за знак границі
Теорема
4.
Якщо послідовності (хп)
і
(уп)
- збіжні (уп)≠0,
n є
N то числова
послідовність
Теорема 5. Якщо послідовність збіжна, то вона обмежена. Теорема 6. Будь-яка обмежена та монотонна послідовність збіжна або, будь-яка обмежена зверху (знизу) неспадна (незростаюча) послідовність збіжна. |
|
має
місце формула:
має
місце формула:
|
Теореми про граничні переходи.
1.
Якщо а>0,
а змінна хп
має скінченну границю, то має місце
формула
2. Якщо а>0, а змінна хп приймає лише додатні значення і має границю, що не дорівнює нулю, то можна переходити до границі під знак логарифма. 3. Якщо змінна хп має скінчену границю, то можна переходити до границі під знак кореня ( у випадку парного числа т припускають, що хп>0 і корінь шукається арифметичний). |
|
1.
2.
3.
|
Правило.
Для того, щоб обчислити границю числової
послідовності при
1. т=к, то границя дорівнює відношенню коефіцієнтів при старших степенях заданих многочленів; 2. m<k, то границя дорівнює нулю; 3. m>k, то границя дорівнює нескінченності. |
|
|
Правило.
Для того, щоб обчислити границю числової
послідовності при
|
Тема: Границя функції неперервного аргументу.
|
f(x)→А при х→х0 |
Геометричний зміст границі. Якщо число А є границею функції y=f(x) при х→х0, то значення функції як завгодно близько наближаються до числа А, коли значення аргумента х як завгодно близько наближаються до числа х0. | |||
|
Якщо
|
Означення
границі функції в точці за Гейне.
Нехай функція
| |||
|
При
|
Означення границі функції в точці за Коші
Нехай
функція
| |||
|
|
Нехай
функція
| |||
|
|
Нехай
функція
| |||
|
Властивості функцій, які мають границю в точці
Теорема
1. Якщо
функція
Теорема
2 (про
граничний перехід у нерівностях).
Якщо в деякому околі точки х0,
крім, можливо, самої точки
х0,
виконується нерівність f(x)≥0
і існує границя
Наслідок.
Якщо в деякому околі точки х0,
крім, можливо, самої точки
х0,
виконується нерівність
Теорема
3 (про
границю проміжної функції).
Нехай функції
Теорема
4. (про
границю монотонної функції).
Якщо функція | ||||
|
Теореми про граничні переходи. | ||||
|
|
1. Якщо число а>0, а функція f(х) має скінченну границю при х→х0 , то можна переходити до границі під знак степеня.
| |||
|
має
місце формула: |
2. Якщо а>0, а функція f(х) приймає лише додатні значення і має границю при х→х0, що не дорівнює нулю, то можна переходити до границі під знак логарифма. | |||
|
має
місце формула:
|
3. Якщо функція f(х) має скінченну границю при х→х0, то можна переходити до границі під знак кореня ( у випадку парного числа т припускають, що f(х)>0 і корінь шукається арифметичний). | |||
|
|
4.
Якщо існують границі
| |||
|
Правила обчислення границь функції в точці та на нескінченності | ||||
|
Якщо
F(х)
= аnхn
+ аn-1xn-1
+ … + а1x+a0,
то
|
1. Границя цілої раціональної функції в заданій точці х0 дорівнює значенню цієї функції в цій точці.
| |||
|
Якщо
x→х0,
|
2. При обчисленні границі дробово-раціональної функції можна в аналітичний вираз функції замість аргумента підставити його граничне значення, якщо при цьому знаменник не перетвориться на нуль. | |||
|
при умові, що Q1(х0)≠0. |
3. Для того щоб обчислити границю дробово-раціональної функції у випадку, коли при х→х0 чисельник та знаменник дробу мають границі, що дорівнюють нулю, необхідно чисельник та знаменник дробу розділити на (х - х0) и перейти до границі. Якщо і після цього чисельник та знаменник нового дробу мають границі рівні нулю при х→ х0, то необхідно виконати повторне ділення на (х – х0) | |||
|
4. Для того щоб обчислити границю дробу, що містить ірраціональні вирази у випадку, коли границя і чисельника і знаменника дробу дорівнює нулю, необхідно перенести ірраціональність із чисельника в знаменник або із знаменника в чисельник і після цього виконати необхідні спрощення (зведення подібних членів, скорочення тощо) та перейти до границі. | ||||
|
5. Для того щоб обчислити границю дробово-раціональної функції у випадку, коли при х→∞ чисельник та знаменник дробу мають границі, що дорівнюють нескінченності, необхідно кожен член многочленів чисельника та знаменника дробу розділити на х в найвищому степені та перейти до границі. | ||||
|
6. Для того щоб обчислити границю функції, що містить ірраціональні вирази у випадку, коли кожен з них має нескінченну границю, необхідно помножити та розділити заданий вираз на вираз, спряжений до нього і після цього виконати необхідні спрощення (зведення подібних членів, скорочення тощо) та перейти до границі. | ||||
|
|
Число
А називається
границею
функції
| |||
|
|
Число
В
називається границею
функції
| |||
|
|
Нехай
функція
| |||
|
|
Перша важлива границя | |||
|
|
Друга важлива границя | |||
|
|
Наслідки з другої важливої границі
| |||
|
Функція
α(x)
називається нескінченно
малою
при х→х0,
якщо для довільного ε>0
існує δ(ε)>0
(М>0), що
для всіх х
таких, що
| ||||
|
Функція
f(x)
називається нескінченно
великою
при х→∞,
якщо для довільного М>0
існує таке число
N=N(М)>0, що
для всіх х
таких, що
| ||||
|
|
функції α1(х) та α2(х) називають нескінченно малими одного порядку при х→х0 | |||
|
|
функції α1(х) називають нескінченно малою вищого порядку, ніж α2(х) при х→х0 | |||
|
|
функції α1(х) називають нескінченно малою нижчого порядку, ніж α2(х) при х→х0 | |||
|
|
функції α1(х) називають нескінченно малою к-го порядку відносно α2(х) при х→х0 | |||
|
Не
існує
|
нескінченно малі функції α1(х) та α2(х) називають непорівнянними при х→х0 | |||
|
|
Функції α1(х) та α2(х) нескінченно малі функції при х→х0 називають еквівалентними нескінченно малими. | |||
|
Властивості еквівалентних нескінченно малих функцій | ||||
|
Теорема 1. Нескінченно малі функції α1(х) та α2(х) еквівалентні при х→х0 тоді і тільки тоді, коли різниця α1(х)-α2(х) є нескінченно малою вищого порядку, ніж кожна з функцій α1(х) та α2(х). | ||||
|
Теорема
2. Нехай
α1(х)
та α1'(х),
α2(х)
та α'2(х)
еквівалентні при х→х0
. Якщо
існує
| ||||
|
Справедливими є такі еквівалентності: х→0
то
| ||||
|
Теорема 3. Сума скінченого числа нескінченно малих функцій різних порядків еквівалентна доданку нижчого порядку. | ||||
|
|
| |||
|
|
|
| ||
|
|
| |||
|
|
| |||
|
|
| |||
|
|
|
| ||
|
|
| |||
|
|
| |||
|
|
| |||
|
|
|
| ||
|
|
|
| ||
|
|
| |||
|
|
| |||
|
|
| |||
|
|
|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
|
| ||

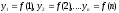 ,
… - відповідно перший, другий , ….
п – ий
члени числової послідовності.
,
… - відповідно перший, другий , ….
п – ий
члени числової послідовності.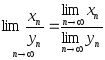 (
(
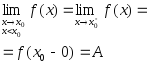
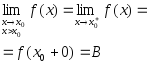
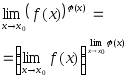
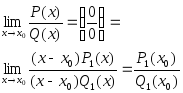
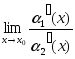 ,
які рівні між собою.
,
які рівні між собою.