
- •Вирівнювання тріангуляції корелатним та параметричним способами
- •Загальні положення
- •1. Вирівнювання ланцюга трикутників між сторонами тріангуляції вищого класу двогруповим корелатним способом
- •Значення виміряних кутів у трикутниках тріангуляції
- •Вихідні координати
- •1.1. Визначення числа умовних рівнянь Розподіл рівнянь на групи та розв’язання рівнянь першої групи
- •Визначення поправок і довжин сторін трикутника
- •Розв’язання оберненої геодезичної задачі
- •1.2. Складання умовних рівнянь другої групи і функцій вирівняних елементів мережі
- •Обчислення дирекційних кутів і координат пунктів ходової лінії
- •Обчислення вільних членів умовних рівнянь координат
- •1.3. Перетворення і розв’язання умовних рівнянь другої групи
- •Перетворені та неперетворені коефіцієнти умовних рівнянь другої групи
- •Вільні члени нормальних рівнянь корелат
- •Коефіцієнти Ni для розв’язання нормальних рівнянь за схемою Гауса
- •1.4. Кінцеві обчислення елементів мережі
- •Розв’язання нормальних рівнянь за схемою Гауса
- •Обчислення остаточно вирівняних сторін і кутів
- •Обчислення координат ходової лінії за вирівняними кутами та сторонами
- •1.5. Оцінка точності вирівняних елементів мережі
- •2. Вирівнювання мережі трикутників тріангуляції параметричним способом
- •2.1. Розв’язання трикутників. Обчислення наближених координат і дирекційних кутів
- •Значення виміряних кутів у трикутниках тріангуляції
- •Координати вихідних пунктів
- •Попередні та кінцеві розв’язки трикутників
- •Обчислення наближених координат пунктів
- •Координати вихідних і визначуваних пунктів
- •2.2. Рівняння поправок напрямків
- •Виміряні напрямки
- •Коефіцієнти та вільні члени поправок напрямків
- •Таблиця коефіцієнтів та вільних членів і рівнянь поправок
- •Коефіцієнти нормальних рівнянь
- •2.3. Складання функцій вирівняних елементів мережі
- •Коефіцієнти вагових функцій
- •2.4. Розв’язання нормальних рівнянь
- •Розв’язання нормальних рівнянь за схемою Гауса
- •Розв’язання нормальних рівнянь за схемою Гауса
- •2.5. Обчислення поправок напрямків
- •Обчислення вирівняних координат
- •2.6. Оцінка точності вирівняних елементів мережі
- •Список літератури
- •Вирівнювання тріангуляції корелатним та параметричним способами
2.2. Рівняння поправок напрямків
Для напрямку , який було виміряно з пункту і на певний пункт К, рівняння поправок записують так:
![]() ,
(2.4)
,
(2.4)
де
![]() -
поправка орієнтирного кутаZіºº
на станції;
-
поправка орієнтирного кутаZіºº
на станції;
![]() поправки до наближених координат
поправки до наближених координат![]() відповідно виражено в дециметрах
відповідно виражено в дециметрах
![]()
![]() ,
(2.5)
,
(2.5)
де
![]() і
і![]() поправки до координат цих пунктів, м;
поправки до координат цих пунктів, м;![]() ,
,![]() – коефіцієнти рівнянь поправок,
– коефіцієнти рівнянь поправок,![]() – вільний член рівнянь поправок.
– вільний член рівнянь поправок.
В
окремих випадках, коли один або два
пункти на кінцях наглядового напрямку
являються вихідними (поправки
![]() і
і![]() до них дорівнюють нулю), рівняння поправок
(2.4) приймають відповідний вигляд. Якщо
направлення змінено з вихідного пунктуі
на визначальний К,
то
до них дорівнюють нулю), рівняння поправок
(2.4) приймають відповідний вигляд. Якщо
направлення змінено з вихідного пунктуі
на визначальний К,
то
![]() ,
(2.6)
,
(2.6)
з пункту і, що визначається на вихідний К
![]()
![]() ,
,
з вихідного пункту і на вихідний пункт К
![]() .
(2.7)
.
(2.7)
Використовуючи формули (2.4) – (2.7), складають рівняння поправок для всіх виміряних напрямків.
Коефіцієнти
![]() ,
,![]() вираховують за формулами
вираховують за формулами
![]() ;
;
![]() ,
(2.8)
,
(2.8)
де
![]() – дирекцій ний кут,
– дирекцій ний кут,![]() – довжина сторони, км.
– довжина сторони, км.
Оскільки
![]() ;
;![]() ,
то в рівняннях поправок для прямого і
оберненого напрямків знаки та величини
цих коефіцієнтів при однойменних
поправках
,
то в рівняннях поправок для прямого і
оберненого напрямків знаки та величини
цих коефіцієнтів при однойменних
поправках![]() і
і![]() будуть попарно однакові, що використовується
в якості контролю.
будуть попарно однакові, що використовується
в якості контролю.
Вільний
член
![]() зрівняння поправок вираховується як
різниця
зрівняння поправок вираховується як
різниця
![]() (2.9)
(2.9)
або
![]() ,
(2.10)
,
(2.10)
де
![]() – дирекційний кут, розрахований з
таблиці 17 за приблизними координатами;
– дирекційний кут, розрахований з
таблиці 17 за приблизними координатами;![]() – приблизно орієнтовне направлення.
– приблизно орієнтовне направлення.
![]() ,
(2.11)
,
(2.11)
де
![]() – значення виміряного напрямку, середнє
зі значень
– значення виміряного напрямку, середнє
зі значень
![]() – орієнтирного кута на станції:
– орієнтирного кута на станції:
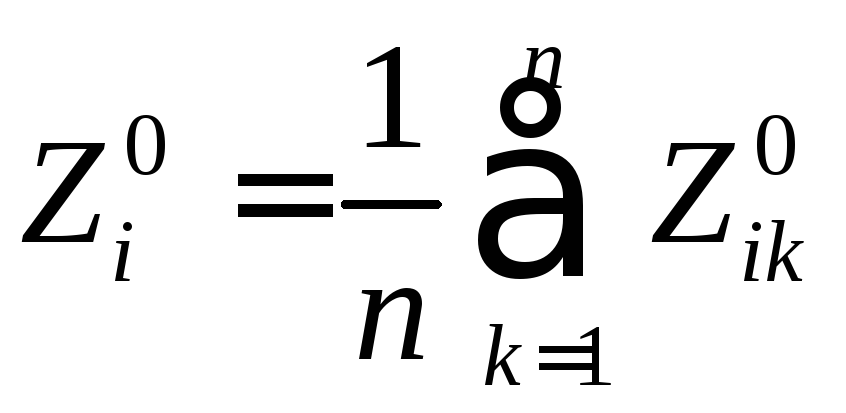 ;
(2.12)
;
(2.12)
![]() ,
(2.13)
,
(2.13)
де n – число виміряних напрямків на пункті.
Таблиця 17
Виміряні напрямки
|
Назва пункту |
Назва напрямку |
Виміряні напрямки |
Градуси |
Радіани | ||
|
1 |
2 |
3 |
4 |
5 | ||
|
A |
AF |
0 |
0 |
0 |
0 |
0 |
|
AB |
73 |
49 |
52,4 |
73,83122 |
1,288598 | |
|
B |
BA |
0 |
0 |
0 |
0 |
0 |
|
BF |
48 |
27 |
41,6 |
48,46156 |
0,845814 | |
|
BE |
111 |
28 |
86 |
111,4906 |
1,945877 | |
|
F |
FC |
0 |
0 |
0 |
0 |
0 |
|
FE |
59 |
10 |
12,4 |
59,17011 |
1,032713 | |
|
FB |
112 |
69 |
62 |
113,1672 |
1,975141 | |
|
FA |
169 |
111 |
83,3 |
170,8731 |
2,982299 | |
|
E |
EB |
0 |
0 |
0 |
0 |
0 |
|
EF |
62 |
58 |
27,5 |
62,97431 |
1,099109 | |
|
EC |
130 |
81 |
44,8 |
131,3624 |
2,292707 | |
|
ED |
176 |
119 |
67,5 |
178,0021 |
3,106722 | |
|
C |
CD |
0 |
0 |
0 |
0 |
0 |
|
CE |
61 |
7 |
59,1 |
61,13308 |
1,066974 | |
|
CF |
113 |
33 |
87,6 |
113,5743 |
1,982246 | |
|
D |
DE |
0 |
0 |
0 |
0 |
0 |
|
DC |
72 |
13 |
42,9 |
72,22858 |
1,260627 | |
Сума значень вільних членів аік на кожній станції дорівнює нулю, як сума відхилень від середнього, що використовується в якості контролю обчислень на станціях.
Сума
поправок
![]() в
напрямки на кожній станції також дорівнює
нулю.
в
напрямки на кожній станції також дорівнює
нулю.
Коефіцієнти та вільні члени поправок напрямків обчислені в таблиці 18.
Потрібно уважно слідкувати за знаками коефіцієнтів а і в, які залежать від величини дирекційного кута.
Значення коефіцієнтів а і в та вільний член l рівнянь поправок виписують з таблиці 18; надаючи кожному рівнянню поправок вагу плюс 1 (P = +1).
Так
як при вирівнюванні користуються
редукційними рівняннями поправок, то
на кожному пункті необхідно дописати
сумарне рівняння з фіктивною вагою P =
![]() – (перше правило Шрейбера), де n
– число напрямків на пункти.
– (перше правило Шрейбера), де n
– число напрямків на пункти.
Нагадаємо порядок складання нормальних рівнянь при параметричному способі вирівнювання. Якщо рівняння поправок записані в загальному вигляді
![]() (і
=1,2,.,n),
(2.14)
(і
=1,2,.,n),
(2.14)
то, відповідні їм нормальні рівняння приймуть вигляд
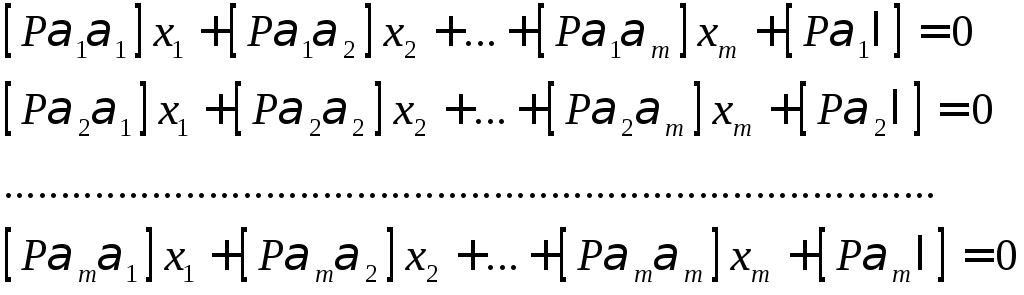 ,
,
де через р = рі позначена вага рівнянь поправок (2.4)
Для нашої мережі рівнянь поправок записані в таблиці 19, а відповідні їм коефіцієнти нормальних рівнянь обчислені в таблиці 20.
Таблиця 18
