Практичне заняття №2

Означення. Події А і В називаються незалежними, якщо поява або непоява однієї з них не впливає на імовірність настання іншої. У супротивному випадку події називаються залежними.

Теорема добутку.

Теорема (добутку імовірностей). Імовірність добутку двох подій А і В дорівнює добутку імовірності однієї з них на умовну імовірність іншої, при умові, що настала перша подія:

Наслідок 1. формули визначення умовних імовірностей. Якщо імовірності подій відмінні від нуля, то

Р_А(В) = Р(АВ)/Р(А) , Р_В(А) = Р(АВ)/Р(В).

Наслідок 2. імовірність добутку двох незалежних подій дорівнює добутку їх імовірностей:

Р(АВ) = Р(А)Р(В).

Наслідок легко розповсюджується на випадок фіксованої кількості співмножників-подій.

Теорема додавання.

Теорема. Імовірність суми двох подій А і В дорівнює сумі імовірностей цих подій без імовірності їх добутку.

Р(А + В) = Р(А) + Р(В) - Р(АВ).

Наслідок 1: Ймовірність суми двох несумісних подій дорівнює сумі іх ймовірностей

P(A+B)= P(A)+ P(B).

Наслідок 2: Ймовірність появи хоча б однієї із подій

P(A+B)=1-P()

Формула повної ймовірності.

Теорема. Нехай подія А може настати лише сумісно з хоча б однією із подій-гіпотез , які утворюють повну групу подій. Тоді ймовірність події А дорівнює:

Формули Байєса.

Теорема. Нехай подія А може настати лише сумісно з хоча б однією із подій-гіпотез , які утворюють повну групу подій. Якщо подія А настала, то умовні ймовірності гіпотез дорівнюють:

Практичне заняття №3

Означення. Випадковою величиною (ВВ) називається величина, яка в результаті випробування в залежності від випадкових обставин може приймати деяке значення.

Означення. Дискретною ВВ називається ВВ, яка приймає окремі ізольовані значення з певними ймовірностями (причому кількість можливих значень або скінчена, або нескінчена, але злічена).

Означення. Неперервною називається така ВВ, яка може приймати всі значення з деякого скінченого або нескінченого проміжку.

Означення. Законом розподілу ДВВ називається відповідність між множиною її можливих значень та їх ймовірностями.

Основними способами завдання ДВВ є табличний, графічний та аналітичний.

Якщо в системі координат Хор відкласти точки та з’єднати їх відрізками отримаємо полігон розподілу ВВ.

Дії над незалежними двв.

Означення. Дві ВВ називаються незалежними, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла інша ВВ.

Означення. Добутком ВВ на сталий множник к називається ВВ kX, яка приймає значення з тими ж ймовірностями, що і ВВ Х.

Означення. K-им степенем ВВ Х називається ВВ , яка приймає значення з тими ж ймовірностями, що і ВВ Х.

Означення. Сумою(різницею або добутком) двох незалежних ВВ X I Y називається ВВ X+Y(X-Y,XY), яка приймає всі можливі значення з ймовірностями , що знаходяться за теоремою добутку.

Числові характеристики двв.

Означення. Математичним сподіванням ДВВ Х називається сума добутків всіх її значень на відповідні ймовірності.

Властивості:

1. М(с)=с

2. М(сХ)=сМ(х)

3. M(X+Y)=M(X)+M(Y)

4. M(XY)=M(X)M(Y)

Означення. Дисперсією ДВВ називається математичне сподівання відхилення ВВ від свого математичного сподівання

Властивості:

1. 

2. D(c)=0

3. 

4. D(X+Y)=D(X)+D(Y)

Означення.Середнє квадратичне відхилення:

Практичне заняття№4.

Означення. Якщо серію випробувань проводити в однакових умовах і імовірність появи подіїв кожному окремому випробуванні однакова та не залежить від появи або непояви подіїв інших випробуваннях, то таку послідовність НПВ називають схемою Бернуллі.

Теорема(Бернулі). Нехай проводиться НПВ за схемою Бернуллі і ймовірність появи подіїв кожному із випробуваньнезмінна (ймовірність непояви подіїв кожному із випробувань). Тоді імовірність того, що подіяз’явитьсяразів уНПВзнаходиться за формулою Бернуллі:

.

Означення. Найімовірнішою частотою (або модою) появи подіїуНПВ називають частоту, для якої.

За означенням із системи умов

неважко дістати подвійну нерівність для визначення найімовірнішої частоти:

.

Теорема (локальна формула Муавра-Лапласа). Якщо у схемі Бернуллі із НПВ імовірність появи подіїдорівнює(), а кількість НПВ досить велика, то імовірність появи подіїразів уНПВ наближено дорівнює (тим точніше, чим більше):

,

де - функція Гауса, а.

Зауваження. Локальна формула Лапласа дає наближені результати тим ближчі до точних, чим більше значення ( при). Це наближення відбувається досить швидко (на практиці формулу застосовують вже навіть при).

Локальна формула Лапласа при малих значеннях дає досить великі похибки, тому в цих випадках застосовують формулу Пуассона.

Теорема Пуассона. Якщо імовірність появи події в кожному із випробувань при необмеженому зростанні кількості НПВ ( ), причому добуток прямує до постійного числа ( ), то імовірність того, що подія з’явиться разів у НПВ задовольняє граничну рівність:

.

На практиці, якщо імовірність постійна і мала, кількість випробувань- досить велика і число- невелике (при ), то користуються наближеною формулою Пуассона:

.

Формулу називають асимптотичною формулою Пуассона.

Практичне заняття №5.

Означення. Інтегральною функцією розподілу ВВ називається імовірність того, що ВВ прийме значення, менше від числа , тобто

.

Означення. ВВ називається неперервною (НВВ), якщо її інтегральна функція неперервна. ВВ називається дискретною (ДВВ), якщо її інтегральна функція розривна (кусочно – стала).

Для ДВВ із множиною значеньфункція розподілу ймовірностей визначається як

,

де символ означає сумування проводиться для всіх можливих значень, які менші від.

ВЛАСТИВОСТІ ФУНКЦІЇ РОЗПОДІЛУ.

1. Значення функції належать проміжку , тобто, причомуНаслідок ( основна формула теорії ймовірностей) :

.

Означення. Щільністю розподілу ймовірностей (або диференціальною функцією розподілу) називається похідна (якщо вона існує) від інтегральної функції розподілу:

Властивості щильності.

1. Щільність розподілу імовірностей – невід’ємна функція, тобто .

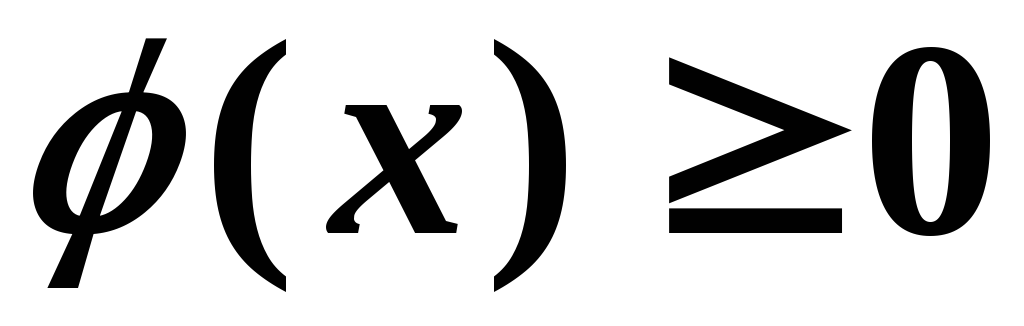2. Теорема .(основна формула теорії імовірностей). Імовірність того, що НВВ прийме значення із деякого проміжказнаходиться за формулою:

.

3. Інтегральна функція розподілу та диференціальна (щільність розподілу імовірностей) є еквівалентними узагальненими характеристиками НВВ, які пов’язані співвідношенням: .

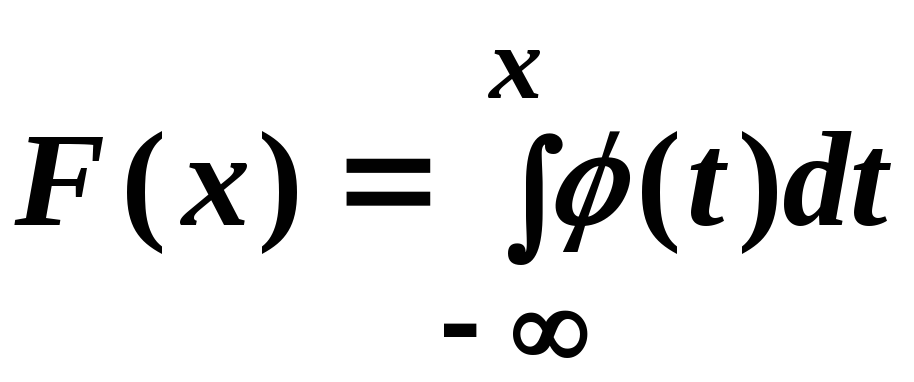Числові характеристики НВВ визначаються наступними формулами (якщо збігаються відповідні невласні інтеграли):