Плотность распределения вероятностей.
Непрерывную с. в. можно задать, используя функцию, которую называют плотностью распределения или плотностью вероятности, или дифференциальной функцией распределения.
Плотностью распределения вероятностей непрерывной с. в. Х называют функцию f(x) – первую производную от функции распределения F(x):
f(x) = F′(x)
Из этого определения следует, что функция распределения является первообразной для плотности распределения.
Для описания распределения вероятностей дискретной с. в. плотность распределения не применима.
Вероятностный смысл плотности распределения.
Таким образом, предел отношения вероятности того, что непрерывная с. в. примет значение, принадлежащее интервалу (x, x +∆x), к длине этого интервала (при ∆x → 0) равен значению плотности распределения в точке х.
Функция плотности характеризует каждое значение непрерывной случайной величины в отдельности, а не целый диапазон как это имеет место для функции распределения.
Вероятность попадания непрерывной с. в. в заданный интервал.
По формуле Ньютона – Лейбница:
P{a < X b}= F(b) – F(a),
таким образом
Нахождение функции распределения по известной функции плотности.
Полагая в предыдущей формуле а = -∞, b = х, и заменив переменную интегрирования х на t имеем:
F(х) = P{X х}=P{-∞< X х},
следовательно
Свойства плотности распределения
Свойство 1. Плотность распределения – неотрицательная функция: f(x)0 (т.к. интегральная функция распределения – неубывающая функция, а плотность распределения ее первая производная).
Свойство 2: 
Доказательство.
Несобственный интеграл
выражает вероятность события, состоящего
в том, что случайная величина примет
значение, принадлежащая интервалу (-∞,
∞). Очевидно, такое событие достоверно,
следовательно, вероятность его равна
единице.
Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью 0х и кривой распределения, равна единице.
В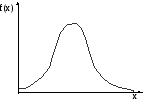
частности, если все возможные значения
случайной величины принадлежат интервалу
(а,b),
то
.
Возможный график плотности распределения (пример)
Задача .
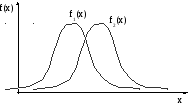
f1(x) – плотность распределения размера выигрыша в 1-й игре
f2(x) – плотность распределения размера выигрыша во 2-ой игре
Какая игра предпочтительней ?
Числовые характеристики случайных величин. .
Данные характеристики позволяют решать многие задачи, не зная закона распределения случайных величин.
Характеристики положения случайной величины на числовой оси.
Математическое ожидание это есть среднее взвешенное значений случайной величины Х, в которое абсцисса каждой точки хi входит с «весом», равным соответствующей вероятности.
Математическое ожидание иногда называют просто средним значением с.в.
Обозначение: mx или M [X].
Для дискретной случайной величины
M
[X]
=
Для непрерывной случайной величины
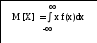
Мода – это наиболее вероятное значение случайной величины (то для которого вероятность pi, или плотность распределения f(x) достигает максимума).
Обозначение:
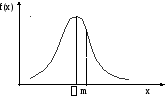
Различают унимодальные распределения ( имеют одну моду), полимодальные распределения ( имеют несколько мод) и анимодальные (не имеют моды)
унимодальное
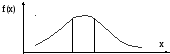
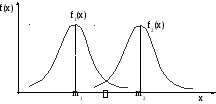
Медиана – это такое значение случайной величины хm, для которого выполняется следующее равенство:
P{X < хm}= P{X > хm}
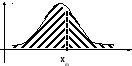Медиана
делит площадь,ограниченную f(x),
пополам
Если плотность распределения случайной величины симметрична и унимодальна, то М[X], и хm совпадают
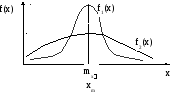
М[X], , хm – неслучайные величины