
Zadanie_1_matn
.docxЗадание 1. По имеющимся данным требуется:
-
Построить статистический ряд распределения. изобразить получившийся ряд графически с помощью полигона или гистограммы. Найти функцию распределения, построить ее график.
-
Найти: выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение выборки, моду и медиану.
-
Проверить при уровне значимости
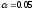 гипотезу о соответствии имеющего
статистического распределения
нормальному закону.
гипотезу о соответствии имеющего
статистического распределения
нормальному закону.
-
Считая данные нормально распределенной случайной величиной найти:
а) точечную оценку математического ожидания изучаемой совокупности;
б) доверительный интервал для математического ожидания с доверительной вероятностью 0.95.
Имеются данные о прибыли коммерческих банков региона, млн. руб.:
|
7.9 |
13.7 |
36.8 |
5.3 |
38.1 |
25.6 |
12.5 |
23.9 |
19.1 |
7.3 |
|
25.1 |
15.4 |
2.0 |
22.1 |
40.3 |
18.0 |
37.5 |
34.0 |
9.7 |
20.3 |
|
23.5 |
13.4 |
26.7 |
0.2 |
28.5 |
0.1 |
37.6 |
27.2 |
34.4 |
13.6 |
|
27.6 |
33.5 |
49.3 |
45.2 |
16.8 |
25.3 |
35.4 |
25.3 |
31.7 |
5.1 |
1. Для полученной выборочной совокупности объемом n=40
а). Производим ранжирование выборочных данных.
|
0.1 |
0.2 |
2.0 |
5.1 |
5.3 |
7.3 |
7.9 |
9.7 |
12.5 |
13.4 |
|
13.6 |
13.7 |
15.4 |
16.8 |
18.0 |
19.1 |
20.3 |
22.1 |
23.5 |
23.9 |
|
25.1 |
25.3 |
25.3 |
25.6 |
26.7 |
27.2 |
27.6 |
28.5 |
31.7 |
33.5 |
|
34.0 |
34.4 |
35.4 |
36.8 |
37.5 |
37.6 |
38.1 |
40.3 |
45.2 |
49.3 |
б) Определяем минимальное и максимальное значение признака.
 млн.
руб.
млн.
руб.
 млн. руб.
млн. руб.
в) Находим размах варьирования признака
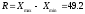 млн.
руб.
млн.
руб.
г) Определяем число групп, на которые разбиваем выборочную совокупность (округление проводим до ближайшего целого)
k =6.
=6.
д) Определяем длину интервала по формуле

е) Определяем границы интервалов и группируем данные по соответствующим интервалам.

|
№ интервала |
Границы интервала
|
Частота
|
Накопленная
частота
|
|
0 |
1 |
3 |
4 |
|
1 |
0.1-8.3 |
7 |
7 |
|
2 |
8.3-16.5 |
6 |
13 |
|
3 |
16.5-24.7 |
7 |
20 |
|
4 |
24.7-32.9 |
9 |
29 |
|
5 |
32.9-41.1 |
10 |
39 |
|
|
41.1-49.3 |
1 |
40 |
|
|
|
40 |
|
ж) На основе полученных данных строим статистический ряд распределения и его геометрические представления.
|
№ Интер вала |
Интервалы
|
|
Частости
|
Накопленныечастости
|
Относительная плотность
распределения
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
1 |
0.1-8.3 |
4.2 |
0.175 |
0.175 |
0.021 |
|
2 |
8.3-16.5 |
12.4 |
0.15 |
0.325 |
0.018 |
|
3 |
16.5-24.7 |
20.6 |
0.175 |
0.5 |
0.021 |
|
4 |
24.7-32.9 |
28.8 |
0.225 |
0.725 |
0.027 |
|
5 |
32.9-41.1 |
37 |
0.25 |
0.975 |
0.03 |
|
|
41.1-49.3 |
45.2 |
0.025 |
1 |
0.003 |
|
|
__ |
__ |
1 |
__ |
__ |
Гистограмма и полигон распределения

Кумулята распределения

2. Найдем выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение выборки, моду и медиану.
а) Вначале находим выборочное среднее, характеризующее центр распределения, около которого группируются выборочные данные, как взвешенное среднее
 млн.
руб.
млн.
руб.
|
№ п./п. |
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
4.2 |
0.175 |
-18.86 |
0.735 |
-3.3 |
62.247 |
|
2 |
12.4 |
0.15 |
-10.66 |
1.86 |
-1.599 |
17.045 |
|
3 |
20.6 |
0.175 |
-2.46 |
3.605 |
-0.43 |
1.059 |
|
4 |
28.8 |
0.225 |
5.74 |
6.48 |
1.292 |
7.413 |
|
5 |
37 |
0.25 |
13.94 |
9.25 |
3.485 |
48.58 |
|
|
45.2 |
0.025 |
22.14 |
1.13 |
0,554 |
12.254 |
|
|
|
1 |
|
23.078 |
0.002 |
148.598 |
Дисперсия
выборочного распределения:


Среднее
квадратическое отклонение
 .
.
В
данном распределении модальным является
интервал (32.9-41.1), так как ему соответствует
наибольшая частота ( ).
Значение моды определим по формуле:
).
Значение моды определим по формуле:
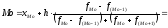

Место
медианы
 ,
поэтому медианным является интервал
(24.8-32.9), так как в этом интервале находятся
номера 20 и 21. Вычислим медиану:
,
поэтому медианным является интервал
(24.8-32.9), так как в этом интервале находятся
номера 20 и 21. Вычислим медиану:


3. Проверим гипотезу о соответствии имеющего статистического распределения нормальному закону. Число наблюдений в крайних интервалах меньше 5, поэтому объединяем их с соседними. Получим:
|
Интервал |
0.1-8.3 |
8.3-16.5 |
16.5-24.7 |
24.7-32.9 |
32.9-49.3 |
|
Частота
,
|
7 |
6 |
7 |
9 |
11 |
Оценки параметров распределения вычислим по выборке:
 ;
;

 ,
,
где

 ,
,
 ,
,
 .
.
Плотность
распределения вероятностей теоретического
распределения на каждом интервале
 рассчитывается по формуле
рассчитывается по формуле
 .
.
Расчеты выполним в табличной форме:
|
№ п./п. |
Интервалы
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0.1-8.3 |
0.175 |
|
-1.21 |
-0.5 |
-0.3869 |
0.1131 |
4.524 |
10.831 |
|
2 |
8.3-16.5 |
0.15 |
-1.21 |
-0.54 |
-0.3869 |
-0.2054 |
0.1815 |
7.26 |
4.958 |
|
3 |
16.5-24.7 |
0.175 |
-0.54 |
0.13 |
-0.2054 |
0.0517 |
0.2571 |
10.284 |
4.764 |
|
4 |
24.7-32.9 |
0.225 |
0.13 |
0.82 |
0.0517 |
0.2939 |
0.2422 |
9.688 |
8.361 |
|
5 |
32.9-49.3 |
0.275 |
0.82 |
|
0.2939 |
0.5 |
0.2061 |
8.244 |
14.677 |
|
|
|
1 |
|
|
|
|
1 |
40 |
43.59 |
Вычисляем
наблюдаемое значение критерия
 :
:
 .
.
Число
степеней свободы по выборке равно
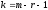 ,
где
,
где
 число интервалов,
число интервалов,
 число параметров распределения, в нашем
случае:
число параметров распределения, в нашем
случае:
 .
.
При
уровне значимости
 и
и
 по таблице распределения
по таблице распределения
 находим
находим
 .
Так как
.
Так как

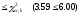 ,
то нет оснований отвергнуть выдвинутую
гипотезу.
,
то нет оснований отвергнуть выдвинутую
гипотезу.
4.
Точечная оценка математического ожидания
найдена при проверке гипотезы о
соответствии распределения нормальному
закону:
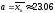 (метод моментов).
(метод моментов).
Доверительный интервал для математического ожидания при известной дисперсии определяется из неравенства:
 ,
,
где
 определяется из уравнения
определяется из уравнения
 .
.
Учитывая,
что
 ,
получаем
,
получаем
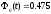 .
По таблице находим
.
По таблице находим
 .
Тогда
.
Тогда
 .
Доверительный интервал для математического
ожидания будет:
.
Доверительный интервал для математического
ожидания будет:
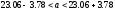
 ,
то есть
,
то есть








 -
-








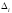








 -
-










