
- •Лабораторная работа №1 Тема: Знакомство с программным продуктом MathCad 2001 Pro
- •Ввод арифметических выражений
- •1.1.2. Знаки арифметических операций
- •Переменные и функции
- •Создание текстовых областей
- •1.4. Задания для самостоятельного решения
- •Лабораторная работа №2 Тема: Работа с массивами данных
- •2.1. Создание и изменение массива
- •2.2. Действия с массивами
- •2.3. Векторные и матричные функции
- •2.4. Задания для самостоятельного решения
- •Лабораторная работа №3
- •3.2. Решение систем уравнений
- •3.3. Решение систем линейных уравнений
- •3.4. Задания для самостоятельного решения
- •Лабораторная работа № 4 Тема: Построение графиков в декартовой системе координат Цели работы:
- •4.1. Построение графиков явно заданных функций
- •4.2. Построение графиков параметрически заданных функций
- •4.3. Задания для самостоятельного решения
- •Лабораторная работа № 5 Тема: Построение графиков в полярной системе координат
- •5.1. Основные теоретические положения
- •5.2. Построение графиков в полярной системе координат при помощи MathCad
- •5.3. Задания для самостоятельного решения
- •Лабораторная работа № 6 Тема: Символьные вычисления
- •Вычисление пределов
- •6.2. Решение систем
- •Преобразование выражений
- •6.4. Задания для самостоятельного решения
- •Лабораторная работа № 7 Тема: Дифференцирование функций одной переменной
- •7.1. Производные первого порядка
- •Задаем функцию:
- •7.2. Производные высших порядков
- •7.3. Задания для самостоятельного решения
- •Список литературы
4.2. Построение графиков параметрически заданных функций
Пусть заданы функции x=(t), y=(t), t(, ). Если при этом x=(t) на интервале (, ) имеет обратную функцию t= -1(x), то определена новая функция y(x)=( -1(x)), называемая функцией, заданной параметрически.
Чтобы построить график функции, заданной параметрически, необходимо:
Определить t как дискретную переменную.
Задать переменные х и у как функции переменной t.
Щелкнуть мышью в свободном месте. Выбрать из меню «Графика» XYPlot (Декартов график).
В появившемся шаблоне напечатать х(t) в среднем поле по оси абсцисс, напечатать y(t) в среднем поле по оси ординат.
Щелкнуть мышью вне графика.
Пример 4. Построим график функции, заданной параметрически соотношениями x=(t+2)3 +10, y=1.5 t 2.
Решение.
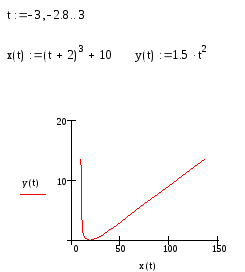
Выведем таблицу значений параметра t и таблицы соответствующих значений х(t) и y(t):

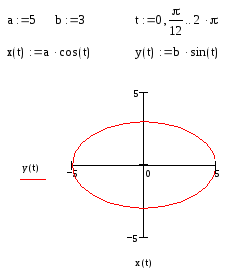
Пример 5. Построим график функции, заданной параметрически соотношениями x=а cos t, y=b sin t, придавая а и b различные значения.
Решение.
1. Пусть а=b=2.

2. Пусть а=5, b=3.
3.
Пусть а=![]() ,
b=
,
b=![]() .
.
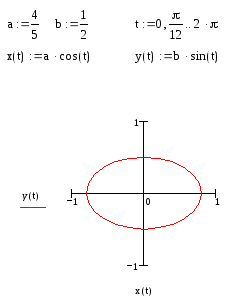
График параметрически заданной функции можно форматировать так же, как и график явно заданной функции.
4.3. Задания для самостоятельного решения
Построить графики явно заданных функций (1) (на различных чертежах);
Построить графики параметрически заданных функций (2):
|
|
(1) |
(2) |
|
1. |
а)
|
|
|
2. |
а)
|
|
|
3. |
а)
|
|
|
4. |
а)
|
|
|
5. |
а)
|
|
|
6. |
а)
|
|
|
7. |
а)
|
|
|
8. |
а)
|
|
|
9. |
а)
|
|
|
10. |
а)
|
|
|
11. |
а) |
|
|
12. |
а)
|
|
|
13. |
а)
|
|
|
14. |
а)
|
|
|
15. |
а)
|
|
|
16. |
а)
|
|
|
17. |
а) |
|
|
18. |
а)
|
|
|
19. |
а)
|
|
|
20. |
а)
|
|
3*.
Построить: а) циклоиду
![]() ,
б) астроиду
,
б) астроиду![]() ,
придавая различные значенияа.
,
придавая различные значенияа.
Лабораторная работа № 5 Тема: Построение графиков в полярной системе координат
Цель работы: Научиться строить графики функций в полярной системе координат.
5.1. Основные теоретические положения
Говорят, что на плоскости задана полярная система координат, если заданы:
-некоторая точка О, называемая полюсом,
-некоторый луч и, исходящий из точки О называемый полярной осью.
Полярными координатами точки М называются два числа:
>0 - полярный радиус, равный расстоянию от точки О до точки М,
-
полярный
угол, равный
углу, на который следует повернуть ось
и
для того, чтобы ее направление совпало
с направлением вектора
![]() (рис. 1).
(рис. 1).

рис. 1.
Запись М(,) означает, что точка М имеет полярные координаты и .
Зададим на плоскости декартову систему координат таким образом, чтобы начало координат совпадало с полюсом полярной системы координат, а направление положительной полуоси абсцисс совпадало с направлением полярной оси (рис. 2).

рис. 2.
Тогда связь между декартовыми координатами точки М(х,у) и полярными координатами этой точки дается формулами:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Уравнение
кривой в полярной системе координат
имеет вид
![]() или
или![]() .
Оно может быть получено либо непосредственно,
исходя из свойств кривой, либо переходом
к полярным координатам в уравнении этой
кривой в декартовой системе координат.
.
Оно может быть получено либо непосредственно,
исходя из свойств кривой, либо переходом
к полярным координатам в уравнении этой
кривой в декартовой системе координат.
Пример
1. Построим
кривую
![]() - спираль Архимеда.
- спираль Архимеда.
Решение.
Будем придавать
значения от 0 до
![]() с шагом
с шагом![]() .
Составим таблицу значений
и
(для вычисления
значений
можно
использовать возможности MathCAD):
.
Составим таблицу значений
и
(для вычисления
значений
можно
использовать возможности MathCAD):
|
j |
0 |
|
|
|
|
|
|
|
|
|
r |
0 |
1.178 |
2.356 |
3.534 |
4.712 |
5.89 |
7.069 |
8.247 |
9.425 |
|
j |
|
|
|
|
|
|
|
|
|
r |
10.603 |
11.781 |
12.959 |
14.137 |
15.315 |
16.493 |
17.671 |
18.85 |
Фиксируем на плоскости точку О и проводим полярную ось и . Выберем также единичный отрезок.
Значению
=0
соответствует =0,
т.е. первая точка кривой – точка О.
Далее проводим из точки О
луч под углом
![]() к полярной оси и отмечаем на этом луче
точку на расстоянии 1.178 от начала
координат. Затем проводим луч под углом
к полярной оси и отмечаем на этом луче
точку на расстоянии 1.178 от начала
координат. Затем проводим луч под углом
![]() и отмечаем точку на расстоянии 2.356, и
т.д. Соединив полученные точки в той
последовательности, в которой их
отмечали, построим кривую.
и отмечаем точку на расстоянии 2.356, и
т.д. Соединив полученные точки в той
последовательности, в которой их
отмечали, построим кривую.


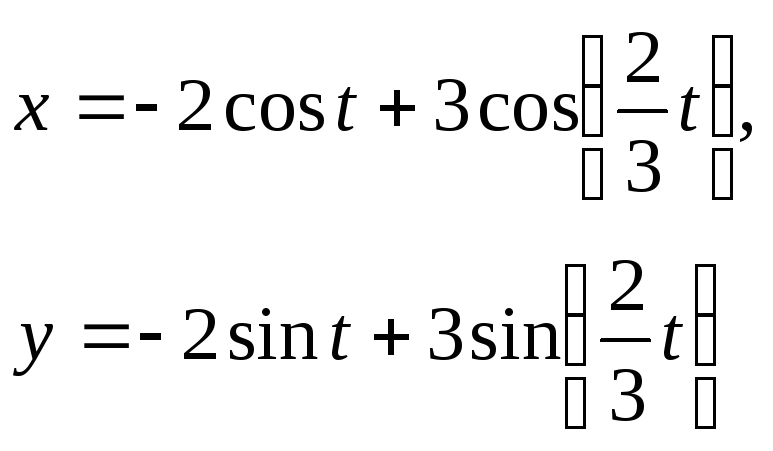
 ;
б)
;
б)