
1 |
|
8 |
|
|
0 |
|
|
0 |
|
|
|
3 |
|
2 |
9 |
0 |
|
||
|
0 |
|
|
|
|
4 |
|
|
|
0 |
|
|
2 |
|
|
5 |
|
7 |
|
|
|
1 |
|
|
|
0 |
|
|
|
6 |
|
Изоморфизм и эквивалентность автоматов |
|
||
Пусть S = (AS, QS, VS, δS, λS) и T = (AT , QT , VT , δT , λT ) — два автомата. |
|||
Тройка отображений f : AS → AT , g : QS → QT , h : VS → VT , называется гомоморфизм автомата S в |
|||
автомат T , если для любых a AS, q QS, v VS выполнены условия |
|||
δT (g(q), f(a)) = g(δS(q, a)) |
|
||
λT (g(q), f(a)) = h(λS(q, a)) |
(4.1) |
||
Автомат T называется гомоморфным автомату S. Если все три отображения сюръективны, то эта трой- |
|||
ка называется гомоморфизмом S на T . Если, кроме того, эти три отображения взаимно-однозначны, то |
|||
они называются изоморфизмом S на T . |
|
|
|
Автоматы, для которых существует изоморфизм, называются изоморфными. Ясно, что мощности |
|||
соответствующих алфавитов изоморфных автоматов должны быть одинаковы. Автоматы S и T изо- |
|||
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель |
|||
морфны, если входы, выходы и состояния S можно переименовать так, что таблица переходов автомата |
|||||
S превратится в таблицу переходов автомата T . |
|
|
|
||
Изоморфизм графов переходов (без учета букв, написанных на ребрах) является необходимым, но |
|||||
недостаточным условием изоморфизма соответствующих автоматов. При гомоморфизме помимо пе- |
|||||
реименования происходит еще и «склеивание» (например нескольких состояний автомата S в одно |
|||||
состояние автомата T ). |
|
|
|
|
|
Пример 4. |
|
|
|
|
|
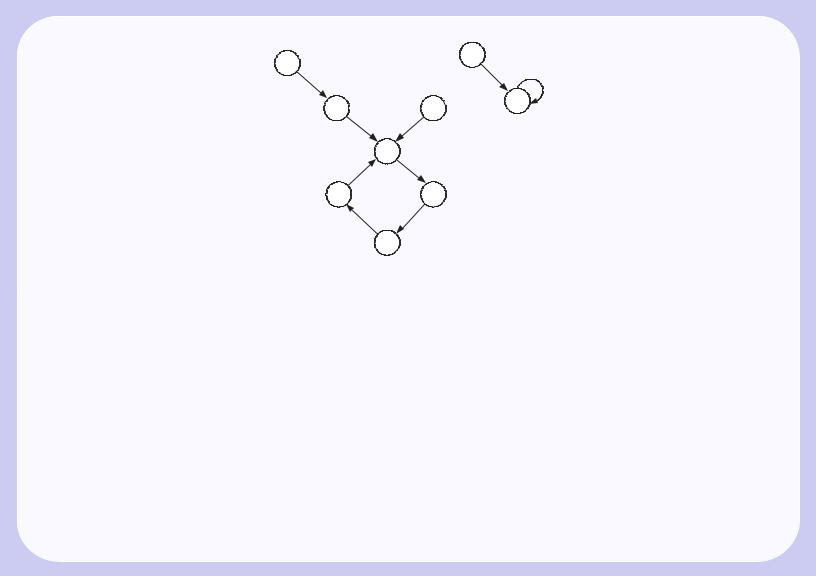
1. В качестве S возьмем автономный автомат из примера 3, а в качестве T — автономный автомат: |
|||||
|
w |
v |
v |
|
|
|
|
|
|
||
r1 |
r2 |
r3 |
|
r4 |
w |
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
v |
|
|
|
r5 |
r6 |
r7 |
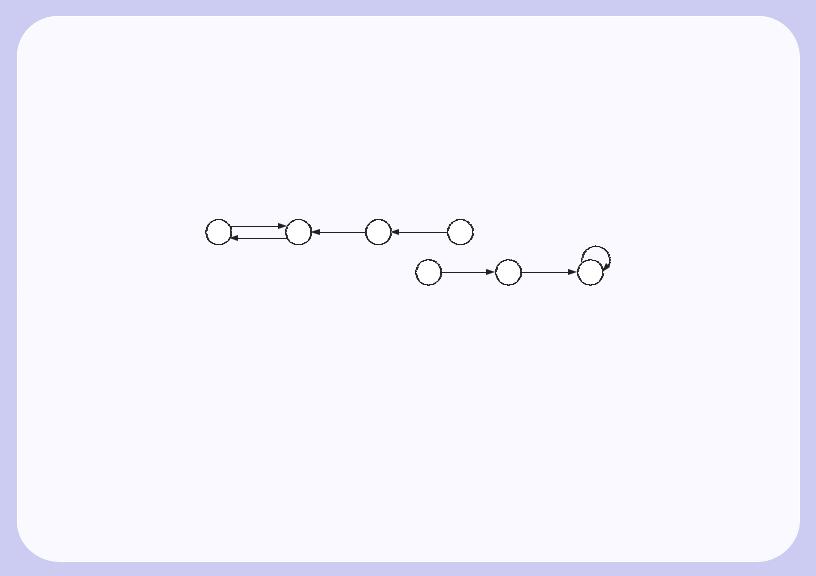
Существует гоморфизм S в T . Соответствующая тройка отображений такова: f тривиально, так |
|||||
как оба входных алфавита состоят из одной буквы, g и h зададим списками (для краткости здесь |
|||||
и в аналогичных случаях вместо qi → rj будем писать i → j); |
|
||||
g = {1 → 4, 2 → 3, 3 → 3, 4 → 2, 5 → 1, 6 → 2, 7 → 1, 8 → 6, 9 → 7}, |
|||||
|
|
|
|
|
h = {0 → υ, 1 → ω, 2 → ω}. |
Никакое состояние S не отобразилось в r5; заметим, что r5 недостижимо из других состояний. |
|||||
Это — общее правило: если состояние T ни входит в область значений g при гомоморфизме, то оно |
|||||
должно быть недостижимым для любого состояния из этой области, иначе нарушается условие (). |
|||||
Если из автомата T состояние r5 вместе с инцидентным ему ребром удалить, то получим новый |
|||||
автомат T 0; описанная тройка отображений является гоморфизмом S в T и S на T 0. Как показывает |
|||||
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель |
|||||

этот пример, число состояний и выходных букв при гомоморфизме может не сохраняться. Для неавтономных автоматов это же относится и ко входному алфавиту.
2. В графе автомата T поменяем местами буквы на двух ребрах: на ребре (r1, r2) напишем v, а на ребре (r2, r1) напишем ω. Получим автомат T 00, граф которого изоморфен графу T ; однако сам автомат T 00 не изоморфен T . Действительно, при изоморфизме графов вершина r4 автомата T изоморфна вершине r4 автомата T 00; однако T (r4, aaa) = vvv, T 00(r4, aaa) = vvω и при любом переименовании выходов в выходном слове T (r4, aaa) все три буквы будут одинаковы, а в T 00(r4, aaa) — нет.
Пусть S и T — два автомата с одинаковыми входными и выходными алфавитами. Состояние q автомата S и состояние r автомата T называются неотличимыми, если для любого входного слова αS(q, α) = T (r, α). В частности, если T = S, то речь идет о неотличимых состояниях одного и того же автомата S. Неотличимость состояний qi и qj автомата S означает, что инициальные автоматы (S, qi) и (S, qj) реализуют одно и то же автоматное отображение.
Автоматы S и T называются неотличимыми, если для любого состояния q автомата S найдется неотличимое от него состояние r автомата T и наоборот, для любого r из T найдется неотличимое от него q из S. Неотличимость автоматов означает, что любое автоматное отображение, реализуемое одним из них, может быть реализовано другим; иначе говоря, их возможности по реализации преобразований входной информации в выходную совпадают. Отношение неотличимости между состояниями и автоматами, как нетрудно показать, рефлексивно, симметрично и транзитивно и, следовательно, является отношением эквивалентности. Обычно неотличимость так и называется эквивалентностью. Переход от автомата S к эквивалентному автомату называется эквивалентным преобразованием автомата S. Можно ставить различные задачи о поиске автоматов, эквивалентных данному и обладающих заданными свойствами. Наиболее изученной является задача о минимизации числа состояний автомата, или, короче, о минимизации автомата: среди автоматов, эквивалентных S, найти автомат с наименьшим числом состояний — минимальный автомат.
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Минимизация автоматов
Теорема (о минимальном автомате). Для любого автомата S существует минимальный автомат S0, единственный с точностью до изоморфизма; если множество состояний S разбивается на l классов
эквивалентности (l 6 n) : C1 = {q11, . . . , q1i1}, . . . , Cl = {ql1, . . . , qlil}, то S0 имеет l состояний.
Если qj1 и qj2 — состояния из одного класса эквивалентности CJ , то для любой входной буквы a состояния δS(qj1, a) и δS(qj2, a) также находятся в одном классе эквивалентности CK . Действительно, если
δS(qj1, a) и δS(qj2, a) не эквивалентны, то найдется слово α, такое что S(δS(qj1, a), α) 6= S(δS(qj2, a), α); но тогда в силу !!! (7-1) S(qj1, aα) 6= S(qj2, aα), то есть qj1 и qj2 не эквивалентны, что противоре-
чит предположению. Учитывая это обстоятельство, определим автомат S0 = (AS, QS, VS, δS0, λS0) так:
QS0 = {C1, . . . , CL}; для любого Ci и любой входной буквы aδS0(Ci, a) = CJ , где CJ — класс эквивалентности, содержащей состояние δS(qir, a)(qir — состояние из Ci; ввиду отмеченного ранее обстоятельства
можно взять любое qir Ci); λS0(Ci, a) = λS(qir, a). Очевидно, что S0 эквивалентен S; попутно заметим, что S0 по построению не имеет эквивалентных состояний. Остается показать, что, во-первых, S0 минимален, а во-вторых, любой минимальный автомат S00 изоморфен S0. Предположим, что S0 не минимален и имеется эквивалентный ему автомат S000 с меньшим числом состояний. По определению неотличимости для каждого состояния S0 найдется эквивалентное ему состояние S000; поскольку в S000 меньше состояний, то какие-то два состояния S0 эквивалентны одному состоянию S000 и в силу транзитивности окажутся эквивалентными между собой, что противоречит отсутствию в S0 эквивалентных состояний. Поэтому S0 минимален. Если же S00 - другой минимальный автомат, то есть имеет то же число состояний, то S00 эквивалентен S0 и различные состояния автомата S00 эквивалентны различным состояниям S0; легко проверить, что это соответствие состояний S0 и S00 и является искомым гомоморфизмом. Теорема доказана.
Однако, чтобы воспользоваться ею для нахождения минимального автомата, нужно уметь находить классы эквивалентных состояний данного автомата. Само определение неотличимости не содержит метода нахождения, так как оно предполагает перебор по бесконечному множеству входных слов.
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Наиболее известным алгоритмом нахождения эквивалентных состояний является алгоритм Мили, который будет описан индуктивно.
Пусть дан автомат S = {A, Q, V, δ, λ} с n состояниями. На каждом шаге алгоритма будем строить некоторое разбиение Q на классы, причем разбиение на следующем шаге будет получаться расщеплением некоторых классов предыдущего разбиения.
Шаг 1 Два состояния q и q0 относим в один класс C1j, если и только если для любого a Aλ(q, a) = λ(q0, a).
Шаг i + 1 Два состояния q и q0 из одного класса Cij относим в один класс Ci+1,j, если и только если для
любого a A δ(q, a) и δ(q0, a) принадлежат одному и тому же классу Cil. Если (i + 1)-й шаг не изменяет разбиение, то есть состояния из одного класса Cij принадлежат одному классу Ci+1,j, то
алгоритм заканчивается и полученное разбиение является разбиением на классы эквивалентных состояний; в противном случае применяем шаг i + 1 к полученному разбиению.
Пример 5. Для автомата S с 9 состояниями и двумя выходными буквами алгоритм строим следующую последовательность разбиений
qi |
a1 |
a2 |
a3 |
|
|
|
|
|
|
|
1 |
2,0 |
4,1 |
4,1 |
|
|
|
|
|
|
|
2 |
1,1 |
1,0 |
5,0 |
(классы отделены точкой с запятой) |
|
|||||
3 |
1,1 |
6,0 |
5,0 |
|
||||||
1 4 6 9; |
2 3 8; |
5 7 |
|
|
|
|||||
4 |
8,0 |
1,1 |
1,1 |
|
|
|
||||
1 4 6; |
9; |
2 3 8; |
5 7 |
|
|
|||||
5 |
6,1 |
4,1 |
3,0 |
|
|
|||||
1 4; |
6; |
9; |
2 3 8; |
5 7 |
|
|||||
6 |
8,0 |
9,1 |
6,1 |
|
||||||
1 4; |
6; |
9; |
2 8; |
3; |
5 7 |
|||||
7 |
6,1 |
1,1 |
3,0 |
|||||||
|
|
|
|
|
|
|||||
8 |
4,1 |
4,0 |
7,0 |
|
|
|
|
|
|
|
9 |
7,0 |
9,1 |
7,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Последнее разбиение является искомым; минимальный для S автомат имеет 6 состояний. Если найденные классы обозначить по порядку C1, . . . , C6 то минимальный автомат описывается таблицей:
ci |
a1 |
a2 |
a3 |
1 |
4,0 |
1,1 |
1,1 |
2 |
4,0 |
3,1 |
2,1 |
3 |
6,0 |
3,1 |
6,1 |
4 |
1,1 |
1,0 |
6,0 |
5 |
1,1 |
2,0 |
6,0 |
6 |
2,1 |
1,1 |
5,0 |
|
|
|
|
Обычно, чтобы избежать составления новой таблицы, в исходной таблице оставляют по одному представителю из каждого класса, а строки остальных состояний вычеркивают; в полученной таблице все вхождения этих остальных состояний также заменяют выбранными представителями. В нашем примере вычеркиваются строки 4, 8, 7; в клетках полученной таблицы 4 заменяется на 1, 8 на 2, 7 на 5, в результате получится таблица:
qi |
a1 |
a2 |
a3 |
1 |
2,0 |
1,1 |
1,1 |
2 |
1,1 |
1,0 |
5,0 |
3 |
1,1 |
6,0 |
5,0 |
5 |
6,1 |
1,1 |
3,0 |
6 |
2,0 |
9,1 |
6,1 |
9 |
5,0 |
9,1 |
5,1 |
|
|
|
|
Поскольку на каждом шаге число классов увеличивается, а общее их число не превосходит n, то описанный алгоритм заканчивается не позднее чем на (n − 1)-м шаге. Докажем теперь, что алгоритм действительно дает разбиение на классы эквивалентных состояний.
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель
