Решение:

Запишем реакцию растворения в ионной форме:

(2.1.6)

Представим ее в виде двух полуреакций (окисления и восстановления):

(2.1.7)

(2.1.8)

Таблица 2.1

Стандартные потенциалы некоторых окислителей металлов

Полуреакция востановления	рН среды	о, В
		+ 1,36
	7	+ 1,23
	14	+ 0,40
	14	- 0,15
	14	+ 0,95
	0	+ 0,69
	0	+ 0,69
		+ 2,87
		+ 2,91
		+ 1,02
	14	+ 1,00
	0	+ 0,77
	0	+ 0,86
		+ 0,54
		+ 0,54
		+ 1,09

.Окислительный потенциал кислорода при его восстановлении по полуреакции (2.7) (см. табл. 2.1). Потенциал золота в растворе его соли(см. табл. 2.2).

В случае отсутствия справочных данных потенциал металла в растворе его соли может быть определен по известным значениям константы нестойкости комплекса по уравнению Нернста.

Таблица 2.2

Стандартные потенциалы благородных металлов в воде и в растворах их солей и константы нестойкости образующихся комплексов

Полуреакция окисления	о, В
	+ 1,88
	+ 1,50
	+ 0,799
	+ 1,2
	+ 0,987
	+ 0,8
	- 0,54	41
	+ 0,15	29,4
	- 0,47	39,9
	+ 0,38	25,5
	+ 0,58	22,1
	+ 1,00	29,5
	+ 0,73	16
	+ 0,76	33
	+ 0,59	13,2
	+ 0,44	19,0
	+ 0,40	29,6
	+ 0,19	24,9
	+ 0,86	20

. Рассмотрим этот расчет.

Применительно к реации (2.1.6) уравнение Нернста примет вид

(2.1.9)

Подставив значения постоянных (R, T, F), ,n и перейдя от натуральных логарифмов к десятичным, получим для золота при 25 ^оС:

(2.1.10)

Значениенайдем через константу нестойкости комплексного иона, равновесие диссоциации которого

сильно сдвинуто влево и характеризуется величиной константы нестойкости:

(2.1.11)

Из уравнения (2.1.11)

Подставим значение в уравнение (2.1.10):

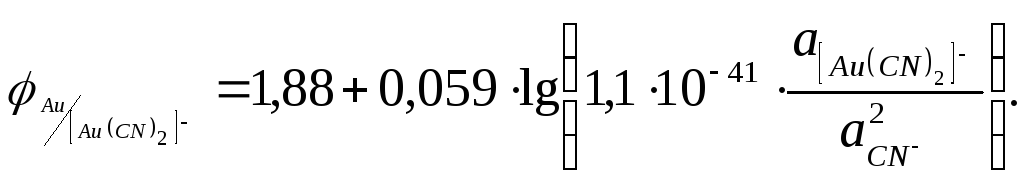
После упрощения получим:

При = 1 истандартный потенциал полуреакции (2.1.8) равен – 0,54 В, т.е..

Так как (- 0,15 В) меньше чем(- 0,54 В), то процесс растворения золота в цианистом растворе в присутствии кислорода термодинамически возможен.

Рассчитаем по уравнениям (2.1.1) и (2.1.2) иК_р реакции:

Высокое значение константы равновесия показывает, что реакция (2.1.6) должна протекать с большой полнотой в сторону растворения золота.