2012 МОК КазГАСА Математика 1 Сыдыкова Д.К.

Казахская головная архитектурно-строительная академия Активный раздаточный материал. Математика: I ФОЕНП Кредит 3 1-й семестр Лекция №1. Матрицы, основные понятия. Определители квадратных матриц 2012/13 уч.год. К.т.н., ассоц. профессор Сыдыкова Дамелькан Какеновна

Краткое содержание лекции.

Матрицей размера называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы обозначаются заглавными буквами латинского алфавита, например A, B, C, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: , где i-номер строки, j-номер столбца.

Например, матрица

или матрица A=(, i=1 ,2, 3, …m, j=1, 2 ,3,…n.

Матрица, состоящая из одной строки, называется матрицей строкой, а из одного столбца – матрицей столбцом: A=( … ) – матрица-строка. Матрица называется квадратной n-го порядка, если m=n.

Элементы матрицы у которых i=j, называются диагональными и образуют главную диагональ матрицы.

Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.

Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, остальные нули, то матрица называется единичной и обозначается Е.

Произведением матрицы А на число λ называется матрица В=λА, элементы которой , для , .

Суммой двух матриц А и В одинакового размера mxn называется С=А+В, элементы которой для , (т.е. матрицы складываются поэлементно).

Разность двух матриц определяется: А – В = А + (-1)·В.

Умножение матрицы А на матрицу В определяется по формуле: , , .

Матрица , называется транспонированной относительно матрицы А в которой строки и столбцы поменялись местами с сохранением порядка.

Определитель матрицы А обозначается или ∆.

Определителем матрицы второго порядка называется число, которое вычисляется по формуле .

Аналогично, вводится определитель третьего порядка. Определителем третьего порядка, называется число, которое вычисляется по формуле

∆==

Минором элемента матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-ой строки и j-го столбца.

Алгебраическим дополнением элемента матрицы n-го порядка называется его минор, взятый со знаком , т.е.

Задание на СРС

1. Свойства определителей. Вычисление определителей 4-го и высших порядков [1,3,4];

Форма отчета: конспект; срок сдачи – 2-ая неделя.

2. ИДЗ -1.1.- 1.2, решение задач по варианту из [ 2 – стр.33 ], срок сдачи – 2-ая неделя.

Задание на СРСП

1. Разложение определителя n-го порядка по элементам какой-либо строки или столбца определителя. Теорема Лапласа [1- стр. ; 3 - с.164; 4 – с.63].

Контрольные вопросы.

1. Как определяется матрица и ее разность? Как обозначается матрица?

2. Какие матрицы называются диагональными, матрицами-строками, матрицами-столбцами и единичными?

3. Как определяется сумма, разность и произведение двух матриц?

4. Какая матрица называется транспонированной?

5. Определение определителя 2-го и 3-го порядков.

6. Что такое минор элемента матрицы n-го порядка?

7. Что такое алгебраическое дополнение элемента матрицы n-го порядка?

Тесты.

1. Вычислите определитель (по Саррюсу): А) -4; B) -2; C) -8; D) -12.

2. Решить уравнение: А) 12; B) -4; C) -10; D) -2.

3. Найти алгебраическое дополнение элемента матрицы А = 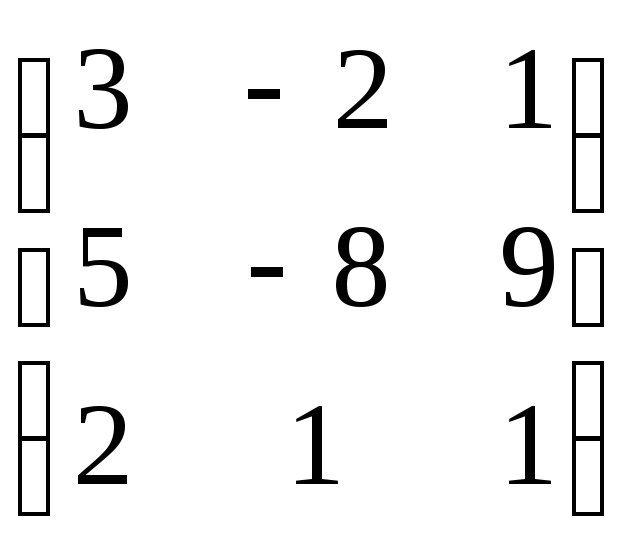. А) 0; B) -1; C) 1; D) 2.

4. Решить уравнение А) 0; 2. B) 0; 1. C) 2; 3. D) -2; 2.

5. Найти минор элемента матрицы А= А) 5; B) -5; C) 7; D) -7.

6. Вычислите определитель, разложив по строке или по столбцу: А) 0; B) 57; C) -32; D) 47.

Глоссарий

№	На русском языке	На казахском языке	На английском языке
1 2 3 4 5 6 7 8 9 10	Матрица Определитель Порядок Свойства Строка Столбец Квадратный Главная диагональ Алгебраическое дополнение Единичная матрица	Матрица Анықтауыш Реті Қасиеті Жатық жол Тік жол, бағана Шаршы Бас диагональ Алгебралық толықтауыш Бірлік матрица	Matrix Determinant Orderliness Properties Line Column Square Main diagonal Algebraic addition Unitary matrix

Список литературы

Основная:

1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М.: Наука 2001;

2. А.Т.Рябушко. Сборник индивидуальных заданий по высшей математике. 1 часть. – Минск: Высшая школа, 2003.

3. К. Кабдыкаир. Курс математики. Алматы, 2005.

Дополнительная:

4. Кудрявцев Л., Демидович Б.П., Краткий курс высшей математики. М.: Наука, 2000.

5. Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, 2002.