Модуль-1 / АРМ №4

2012 КазГАСА Математика 1 Сыдыкова Д.К..

Казахская Головная Архитектурно- Строительная Академия.

Активный раздаточный материал.

Математика 1 ФОЕНП

Кредит 3 1-ый семестр

Лекция №4. Скалярные и векторные произведения векторов. 2012/13 уч. г.

К.т.н., ассоц. профессор Сыдыкова Дамелькан Какеновна.

Краткое содержание лекции

Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла φ между ними: () = = ||×||×cosφ

Скалярное произведение обладает следующими основными свойствами:

1. Скалярное произведение двух векторов не зависит от порядка этих сомножителей (переместительное свойство): =

2. Распределительное свойство. (+)= + .

3. Скалярный квадрат вектора равен квадрату модуля этого вектора, т. е. ²= ||²

4. Скалярный множитель можно выносить за знак скалярного произведения, т. е. (λ ) = (, λ) = λ()

5. Скалярное произведение линейной комбинации векторов на произвольный вектор равно такой же линейной комбинации данных векторов на этот вектор, т. е. (λ + μ, ) = λ(,) + μ(, )

Косинус угла φ=() между двумя ненулевыми векторами и равен cosφ= .

Два вектора и перпендикулярны тогда и только тогда, когда

Пусть =a_x + a_y + a_z и =b_x + b_y + b_z, тогда =a_xb_x+a_yb_y+a_zb_z, здесь учтены, что = = = 0 и = = = 1

Поэтому косинус угла φ между двумя векторами и определяется cosφ= (a_xb_x+a_yb_y+a_zb_z)/ (||||)

Для перпендикулярных векторов и имеем φ=π/2 и, следовательно, cosφ=0, или a_xb_x+a_yb_y+a_zb_z=0.

Под векторным произведением двух векторов и понимается вектор =×=[a.b], для которого:

1. Модуль равен площади параллелограмма, построенного на данных векторах, т.е. |c| = |a | |b|sinφ,где φ=∟(), (0≤φ≤π) (рис 4.1);

рис 4.1

2. Этот вектор перпендикулярен перемножаемым векторам, т. е. _┴ и _┴ ;

3. Если векторы неколлинеарные, то векторы ,образуют правую тройку векторов.

Основные свойства векторного произведения.

1. При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т. е. ×=-(×)

2. Векторный квадрат равен нуль-вектору, т. е. ×=0

3. Скалярный множитель можно выносить за знак векторного произведения, т. е. если λ-скалярное, то (λ×) = (×λ) = λ(×)

4. Для любых трёх векторов a,b,c справедливо равенство (+)×=()+()

Необходимым и достаточным условием коллинеарности двух векторов и : ×=0

Пусть =a_x + a_y + a_z и =b_x + b_y + b_z, тогда

×=| a_y a_z| - | a_x a_z| +| a_x a_y|

| b_y b_z| |b_x b_z| | b_x b_y |

Для удобства последняя формула записывается в виде определителя третьего порядка

| |

×= | a_x a_y a_z|

|b_x b_y b_z|

Под смешанным произведением и понимается число

Построим параллелепипед (рис 4.2),

рис 4.2

Ребрами которого, исходящего из общей вершины О, являются векторы и . Тогда |×|=S представляет собой площадь параллелогромма, построенного на векторах и , т. е. площадь основания параллелипипеда. Высота этого параллелипипеда равна H= ±nр = ±|| cosφ, где =× и знак плюс соответствует острому углу φ=∟(,), а знак минус тупому углу φ. В первом случае векторы , образуют правую тройку, а во втором- левую тройку. Поэтому = = S np=±V, т. е. объём параллелипипеда, построенного на векторах , . Отсюда =±V.

Основные свойства смешанного произведения

1. == 2. ====-

Необходимым и достаточным условием компланарности трёх векторов , : =0

Если = a_x + a_y + a_z, =b_x + b_y + b_z, =с_x + с_y + с_z то

| a_x + a_y + a_z|

• =| b_x+ b_y + b_z|

| с_x + с_y + с_z|

Задание на СРС

1. Свойства скалярного, векторного и смешанного произведения векторов [1, 3, 4]

Форма отчёта: конспект, срок 6 дней.

2. Решить задачи, из [2, стр.274, № 2, 4, 5] .

Задание на СРСП

1. Линейная зависимость векторов [1,3]

Контрольные вопросы:

А. Для письменного контроля

1. Что такое скалярное произведение двух векторов?

2. Основные свойства скалярного произведения векторов и

3. Как определяется скалярное произведение векторов =(a_x, a_y, a_z) и (b_x, b_y, b_z)?

4. Условие перпендикулярности векторов =(a_x, a_y, a_z) и (b_x, b_y, b_z)

5. Как определяется векторное произведение векторов и ?

6. Основные свойства векторного произведения ×?

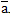7. Как определяется ×, если =(a_x, a_y, a_z) и (b_x, b_y, b_z)?

8. Необходимое и достаточное условие коллинеарности векторов и

9. Как понимается смешанное произведение векторов и ?

10. Основные свойствва смешанного произведения

11. Как определяется если =(a_x, a_y, a_z), (b_x, b_y, b_z) и (с_x + с_y + с_z)?

12. Необходимое и достаточное условие компланарности векторов , ?

Б. Для компьютерного тестирования

1. Вычислить косинус угла, образованного векторами =(2; -4; 4) и (-3; 2; 6).

А) 2; В) 2/3; С) 4; Д) 5/21; Е)3/5;

2. Даны векторы =(-4; -2;-4) и (6;-3;2). Вычислить: (2-3)(+2).

А)40; В)2/3; С)4; Д)-200; Е)5

3. Даны точки А(1; 2; 0), В(3; 0; -3) и С(5; 2; 6). Вычислить площадь треугольника АВС.

А) 50 кв. ед.; В) 14 кв.ед. С) 25 кв.ед.; Д)40 кв. ед.; Е) 45 кв. ед.

4.Дано, что ||=3, ||=5. Определить, при каком значении ά векторы +2,-2, будут взаимно перпендикулярны.

А) ±2; В) 2/7; С) ±3/5; Д) 4; Е) ±5.

5. Даны вершины треугольника А(-1;-2;-4), В(-4;-2;-0)и С(3;-2;1). Определить его внутренний угол при вершине В.

А) 30º; В) 35º; С) 40º; Д) 45º; Е) 50º;

6. Даны три вектора: =(1;-1;3), =(-2;2;1), =(3;-2;5). Вычислить смешанное произведение .

А) -3; В) 5; С) -7; Д) 8; Е) 1;

Глоссарий

№	На русском языке	На казахском языке	На английском языке
1	Смешанное	Аралас	Mixed
2	Произведение	Көбейту	Product
3	Скалярное произведение	Скалярлық көбейту	Scalar product
4	Свойство	Қасиеті	Property
5	Площадь	Аудан	The area
6	Основные	Негізгі	Basic
7	Площадь основания	Табан ауданы	The area of the basic
8	Необходимый	Қажетті	Necessary
9	достаточный	жеткілікті	Suffisient

Список литературы

Основная:

1. Бугров А. С., Никольский С. М. «Элементы линейной алгебры и аналитической геометрии»-М:Наука 2002

2. Рябушко А.П. ИДЗ по ВМ - М: Наука, 2003

3. К. Кабдыкаир. Курс математики. Алматы, 2005.

4. Д.К. Сыдыкова Математика-1. Методическое руководство по выполнению заданий для СРС. КазГАСА, 2008.

Дополнительная:

5. В. Е. Шнейдер и др «Краткий курс высшей математики» 1,2 том.- М: Высшая школа, 2000

6. Д. В. Клетник «Сборник задач по аналитической геометрии» М.Наука, 2001