Auto CAD2011 KazGASA / 16

Жунусов Абдулла Шегебаевич, Буганова Светлана Николаевна

AutoCAD 2011 КазГАСА

АРМ(тренинг) № 16

Метрические задачи Начертательной геометрии

Задана плоскость ABC и точка D, где построены горизонталь (h₁, h₂) и фронталь ( f₂, f₁) плоскости ABC (смотри АРМ № 15), также установлен Формат А3.

1.Построим плоскость ( h¹ , f¹ ), проходящую через точку D и параллельную заданной плоскости ABC.

Теорема. Если две плоскости параллельны между собой, то две прямые одной плоскости параллельны двум прямым другой плоскости. В качестве этих двух прямых можно взять их горизонталь h и фронталь f.

Проведем ( ║; ║) и ( ║ ; ║ ), для чего включим объектные привязки: «конточка» и

отрезок> точка D₁> ознакомить c f₁> провести > EE

> точка D₁> орто> провести > EE

> точка D₂> ознакомить с f¹₂> провести >EE

>точка D₂> орто> провести h¹₂

2. Построим плоскость (h¹ , f¹), проходящую через точку D и перпендикулярную заданной плоскости ABC.

Теорема. Если две плоскости перпендикулярны между собой, то одна прямая одной плоскости перпендикулярна двум прямым другой плоскости.

В качестве одной прямой заданной плоскости можно взять любую сторону треугольника (например AС). В качестве двух прямых конструируемой плоскости можно взять её горизонталь h¹ и фронталь f¹.

П

Отрезок > точка D₁> указать A₁С₁ (появиться знак )>EE(построена f¹₂)

> точка D₁> орто> провести >EE

> точка D₂> указать A₂ C₂ (появиться знак )> EE(построена h¹₂)

> точка D₂> орто> провести > EE

роведем ( ║h; ┴ A₁ С₁) и ( ┴ A₂ С₂ ; ║f₂ ), для чего включим объектные привязки: «конточка» и

Новая плоскость (h¹ f¹) перпендикулярна заданной плоскости ABC, так как две прямые (h¹ и f¹) перпендикулярны прямой AС.

3. Найдем расстояние от точки D до плоскости ABC.

Чтобы решить задачу опустим перпендикулярную к плоскости прямую ДК, проходящую через точку D, построим пересечение этого перпендикуляра с плоскостью ABC в точке К, затем определим натуральную величину отрезка DК.

Теорема. Если прямая перпендикулярна плоскости ,то фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (D₁ K₁ ┴ f₁) , а горизонтальная проекция – горизонтальной проекции горизонтали плоскости (D₂ K₂ ┴ h₂).

Включим объектные привязки «конточка» , > указать f₁ ( 3_1, 4₁ )(появится значок )> ЕЕ> D₂> указать h₂ ( 1₂2₂)(появится значок )> ЕЕ (построены направления отрезка DK). Пока точки К нет.

Для нахождения точки К ( К₁,К₂ ) ,построим плоскость сечения, проходящую через направления DK и находим пересечение 5,6,затем точку К как пересечение этой линии с перпендикуляром . Для этого включим объектную привязку (если отключена ), затем:

Отрезок>щелкнем по D₂> продолжим перпендикуляр> щелкнем в точках 6₂ и 5₂( получили пересечение)>

>5₂> орто> вверх до точки 5₁>ЕЕ>

>6₂>орто> вверх до точки 6₁>ЕЕ>

> 5 ₁>6₁> ЕЕ(построена фронтальная проекция пересечения).

Находим К ₁ как пересечение 5₁6₁ с перпендикуляром DK₁ ,затем:

отрезок> K₁> орто> вниз до точки K₂( D ₂K ₂- горизонтальная проекция ,D ₁K ₁-фронтальная проекция перпендикуляра.

Для нахождения натуральной величины отрезка DK, используем меню «Параметризация», которое появилось в последней версии Auto CAD 2010:

Сначала определим разность ординат, для чего: > Орто> K₂> вправо до точки D(появится привязка )>Е E> указать D> указать D₂>EE ( DD ₂-разность ординат).

Перенесём отрезок D D₂ в точку D_{1 ,} для чего: Меню «Параметризация»> «Геометрическая зависимость»> «Совпадение»> D₁ > D₂ (отрезок D D₂ переносится в DD ₁).

Установим D D₁ перпендикулярно к D₁K₁ , для чего: Меню «Параметризация» >«Геометрическая зависимость»>«Перпендикулярность»> D₁ K₁> D D₁( стали перпендикулярны)> > K₁> D> EE ( K ₁ D-натуральная величина отрезка ).

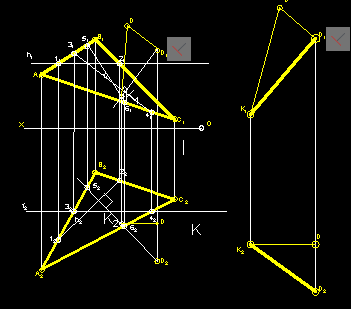
Построена натуральная величина (K₁D) расстояния от точки D до плоскости ABC.

Сохраним чертёж под именем «АРМ № 16 Расстояние от точки D до плоскости ABC» или продолжим АРМ №17.