
- •Дифференциальные уравнения
- •Теория рядов
- •Вопрос 023 Выражение вида называется бесконечным … Ответ числовым рядом
- •Теория вероятности и мат.Статистика
- •Вопрос 187 Имеется 10 заклепок. Из них 5 железных, 3 медных и 2 латунных. Наудачу взято две заклепки. Какова вероятность того, что они железные? Ответ 2/9
- •Вопрос 189 Имеется 10 заклепок. Из них 5 железных, 3 медных и 2 латунных. Наудачу взято две заклепки. Какова вероятность того, что они медные? Ответ 1/15
- •Вопрос 191 Имеется 10 заклепок. Из них 5 железных, 3 медных и 2 латунных. Наудачу взято две заклепки. Какова вероятность того, что они латунные? Ответ 1/45
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
-
Вопрос 283 Найти область определения функции:
 Ответ полусфера
с радиусом равным 3
Ответ полусфера
с радиусом равным 3 -
Вопрос 284 Найти производную функции
 в
точке
в
точке
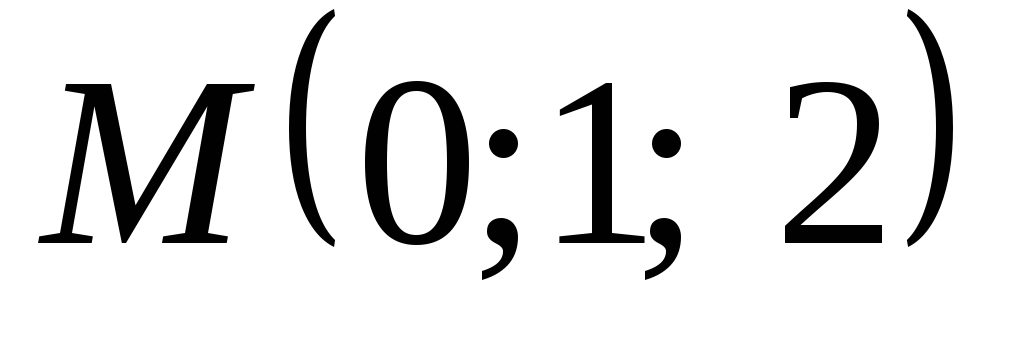 в направлении от точки к точке
в направлении от точки к точке
 ?
Ответ
?
Ответ

-
Вопрос 285 Найти область определения функции:
 Ответ
Ответ

-
Вопрос 102 Найти
 , если
, если
 Ответ
Ответ

-
Вопрос 295 Найти частную производную функции
 по х: Ответ
по х: Ответ

-
Вопрос 296 Найти частную производную функции
 по
y: Ответ
по
y: Ответ

-
Вопрос 297 Найти частную производную функции
 по x: Ответ
по x: Ответ
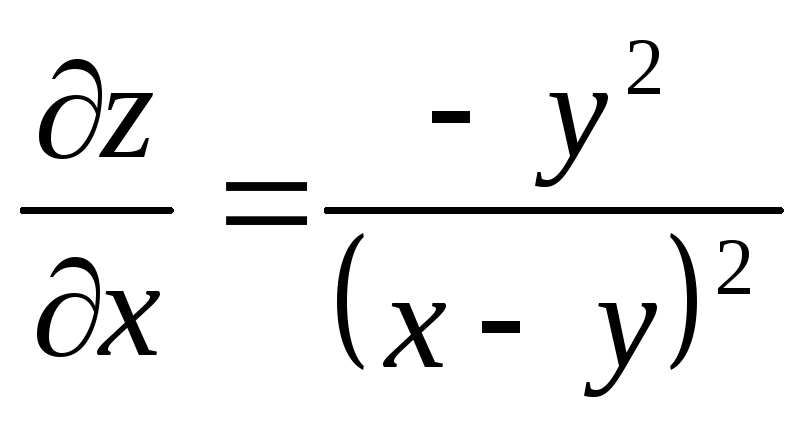
-
Вопрос 298 Найти частную производную функции
 по x:
Ответ
по x:
Ответ

-
Вопрос 299 Найти частную производную функции
 по x:
Ответ
по x:
Ответ

-
Вопрос 300 Найти частную производную функции
 по x:
Ответ
по x:
Ответ

-
Вопрос 301 Найти частную производную функции
 по х: Ответ
по х: Ответ

-
Вопрос 302 Найти частную производную функции
 по х: Ответ
по х: Ответ

-
Вопрос 308 Найти частную производную функции
 по у: Ответ
по у: Ответ

-
Вопрос 309 Найти частную производную функции
 по у: Ответ
по у: Ответ

-
Вопрос 310 Найти частную производную функции
 по у: Ответ
по у: Ответ

-
Вопрос 311 Найти частную производную функции
 по y:
Ответ
по y:
Ответ

-
Вопрос 312 Найти частную производную функции
 по z:
Ответ
по z:
Ответ

-
Вопрос 313 Найти частную производную функции
 по x: Ответ
по x: Ответ

-
Вопрос 314 Найти частную производную функции
 по y: Ответ
по y: Ответ

-
Вопрос 315 Найти частную производную функции
 по у: Ответ
по у: Ответ

-
Вопрос 316 Найти частную производную функции
 по z:
Ответ
по z:
Ответ

-
Вопрос 318 Найти частную производную функции
 по у: Ответ
по у: Ответ
 .
.
-
Вопрос 103 Найти
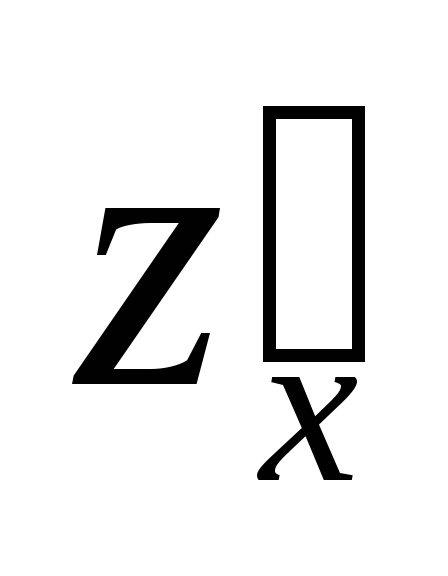 в точке М(1;1), если
в точке М(1;1), если
 Ответ
Ответ

-
Вопрос 104 Найти
 в точке М(0;0;1), если
в точке М(0;0;1), если
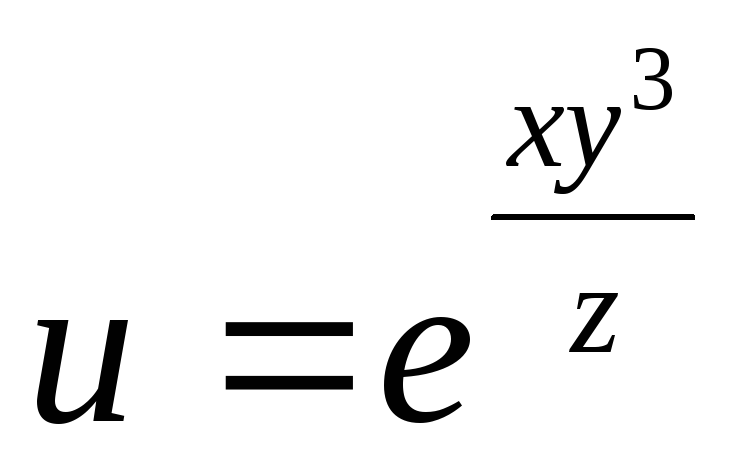 Ответ 0
Ответ 0 -
Вопрос 125 Дана функция
 .
Найти
.
Найти
 .
Ответ
.
Ответ

-
Вопрос 166 Дана функция
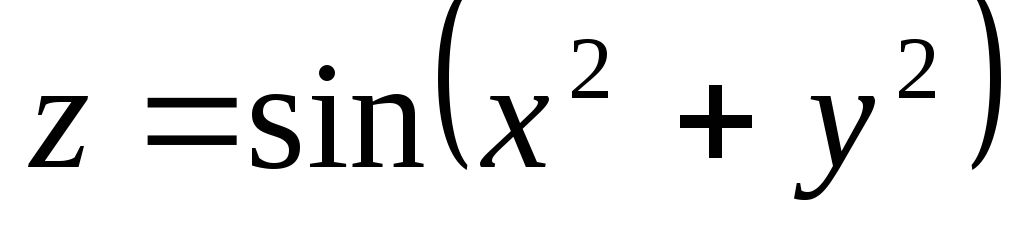 .
Найти
.
Найти
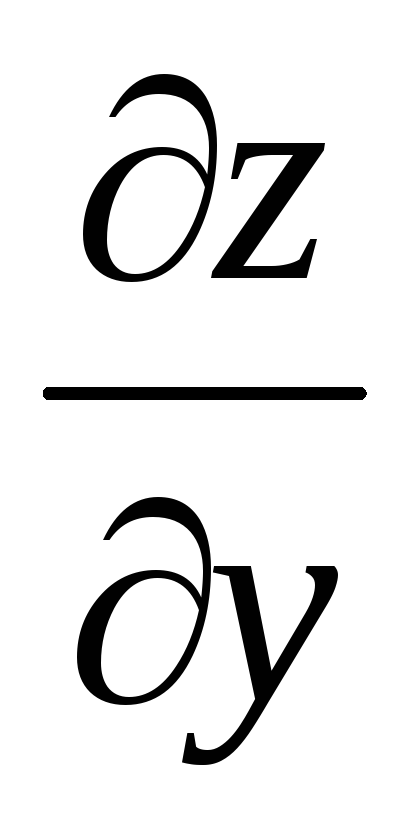 Ответ
Ответ

-
Вопрос 217 Найти частную производную по х в точке (0; 1) функции
 Ответ 2
Ответ 2 -
Вопрос 218. Найти частную производную по х в точке ( 1; 1) функции
 Ответ 4
Ответ 4 -
Вопрос 219. Найти частную производную по х в точке (1; 0) функции
 Ответ 3
Ответ 3 -
Вопрос 220. Найти частную производную по х в точке (-1; 0) функции
 Ответ 0
Ответ 0 -
Вопрос 230. Найти производную
 ,
если
,
если
 .
Ответ
.
Ответ

-
Вопрос 231. Найти частную производную функции по у в точке М( 1; 2 ), если
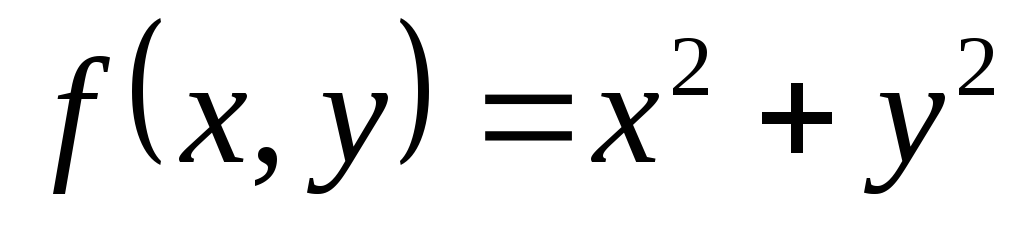 .
Ответ 4
.
Ответ 4 -
Вопрос 232. Найти производную
 в точке М(2;3), если
в точке М(2;3), если
 Ответ
Ответ

-
Вопрос 241 Найти частную производную по у в точке (1;0) функции
 Ответ 4
Ответ 4 -
Вопрос 242. Найти частную производную по у в точке ( 1; 1) функции
 Ответ -1
Ответ -1 -
Вопрос 243. Найти частную производную по у в точке (0; 1) функции
 Ответ 3
Ответ 3 -
Вопрос 244. Найти частную производную по у в точке (-1; 0) функции
 Ответ 0
Ответ 0 -
Вопрос 275 Найти
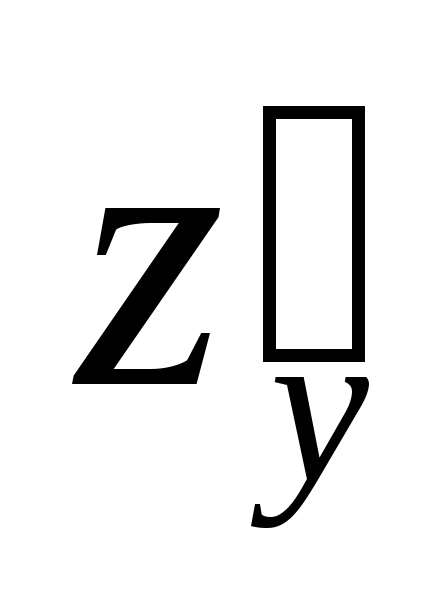 в точке М(1;1), если
в точке М(1;1), если
 Ответ
Ответ

-
Вопрос 276 Найти
 в точке М(0;0;1), если
в точке М(0;0;1), если
 Ответ 0
Ответ 0 -
Вопрос 274 Найти
 , если z=
, если z= Ответ
Ответ
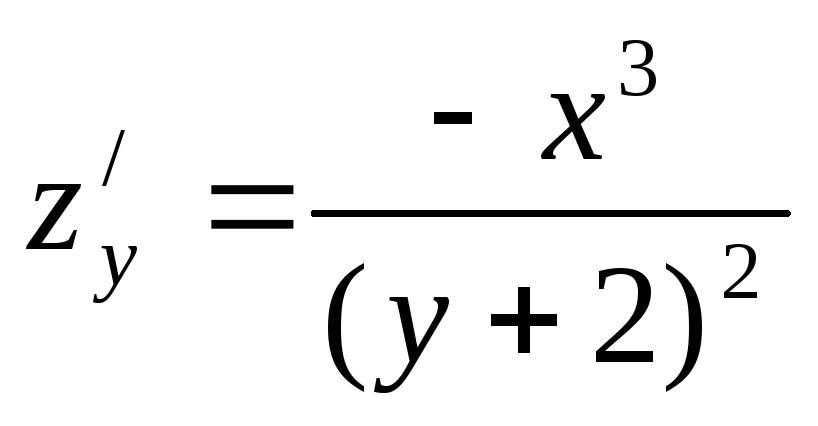
-
Вопрос 192 Написать уравнение касательной плоскости к поверхности параболоида
 в точке
в точке
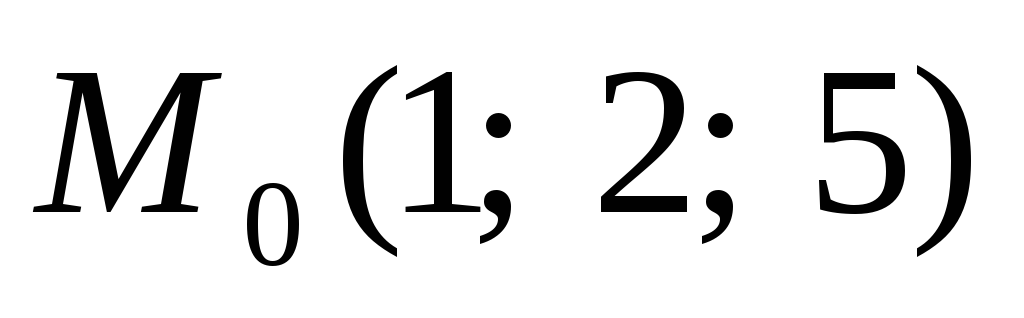 .
.
-
Ответ

-
-
Вопрос 198 Написать уравнение нормали к поверхности параболоида
 в точке
в точке
 .
.-
Ответ

-
-
Вопрос 199 Приращение функции
 по переменной х
называют частным приращением функции
по переменной х
называют частным приращением функции
 по х и
обозначают ...
по х и
обозначают ...-
Ответ

-
-
Вопрос 203 По какой формуле определяется градиент функции
 ?
?-
Ответ

-
-
Вопрос 211 Приращение функции
 по переменной у
называют частным приращением функции
по переменной у
называют частным приращением функции
 по у и
обозначают ...
по у и
обозначают ...-
Ответ

-
-
Вопрос 228. Приращение функции
 по переменной х
и у называют
полным приращением функции
по переменной х
и у называют
полным приращением функции
 и обозначают ... Ответ
и обозначают ... Ответ

-
Вопрос 249 Если функция
 в точке
в точке
 имеет непрерывные производные:
имеет непрерывные производные:
 ,
,
 ;
;
 ,
то в этой точке экстремум может быть,
а может и не быть, если … Ответ
,
то в этой точке экстремум может быть,
а может и не быть, если … Ответ

-
Вопрос 252 Если функция
 в
точке
в
точке
 имеет непрерывные производные:
имеет непрерывные производные:
 ;
;
 ;
;
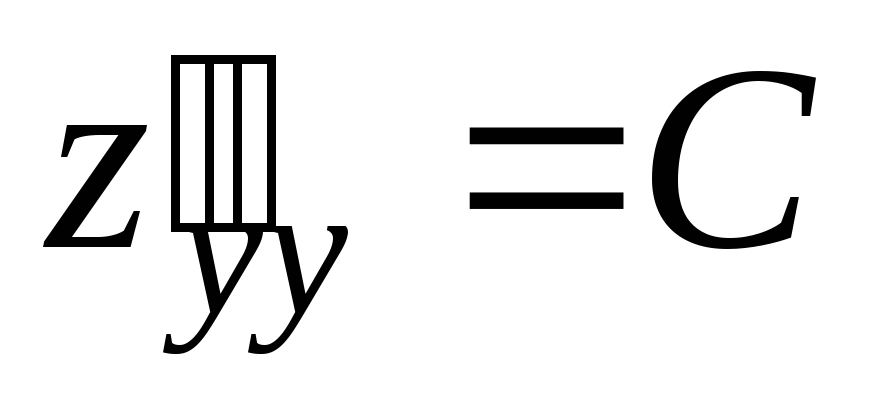 ,
то в этой точке она имеет минимум, если
Ответ
,
то в этой точке она имеет минимум, если
Ответ

-
Вопрос 254 Если функция
 в точке
в точке
 имеет непрерывные производные:
имеет непрерывные производные:
 ,
,
 ;
;
 ,
то в этой точке она имеет максимум, если
… Ответ
,
то в этой точке она имеет максимум, если
… Ответ

-
Вопрос 256 Если функция
 в точке
в точке
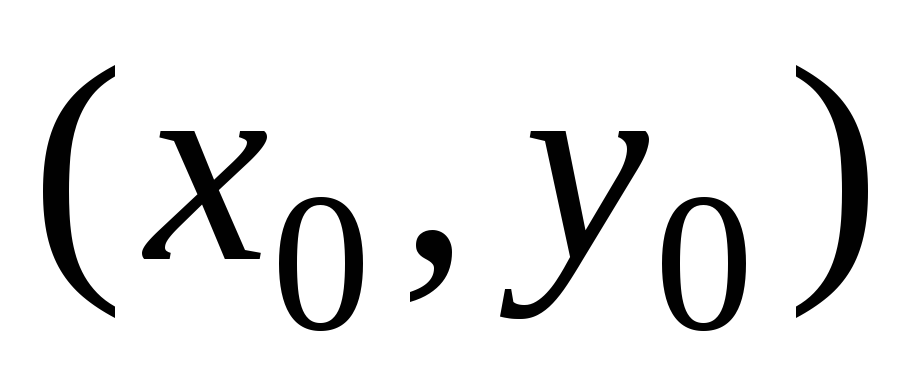 имеет непрерывные производные:
имеет непрерывные производные:
 ,
,
 ;
;
 ,
то в этой точке она не имеет экстремума,
если … Ответ
,
то в этой точке она не имеет экстремума,
если … Ответ

-
Вопрос 265 По какой формуле определяется производная функции
 в
точке
в
точке
 в направлении вектора
в направлении вектора
 ?
Ответ
?
Ответ

-
Вопрос 266 Если функция
 в критической точке
в критической точке
 имеет непрерывные частные производные
второго порядка удовлетворяющие
условию:
имеет непрерывные частные производные
второго порядка удовлетворяющие
условию:
 и
и
 ,
то в этой точке она имеет …
,
то в этой точке она имеет …-
Ответ максимум
-
-
Вопрос 267 Если функция
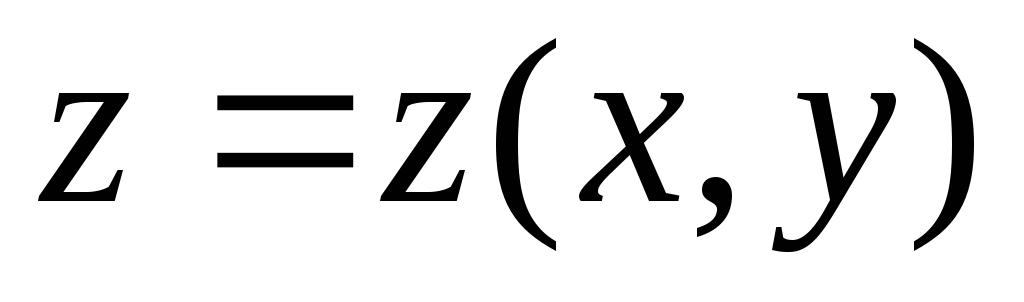 в критической точке
в критической точке
 имеет непрерывные частные производные
второго порядка, удовлетворяющие
условию:
имеет непрерывные частные производные
второго порядка, удовлетворяющие
условию: и
и
 ,
то в этой точке она …
,
то в этой точке она …
-
Ответ не имеет экстремума
-
-
Вопрос 272 Записать формулу для вычисления площади фигуры, ограниченной линиями
 ,
,
 ,
через двойной интеграл Ответ
,
через двойной интеграл Ответ

-
Вопрос 277 Записать через двойной интеграл формулу для вычисления площади фигуры, ограниченной линиями
 ,
,
 ,
и
,
и
 Ответ
Ответ

-
Вопрос 278 Вычислить двухкратный интеграл
 Ответ 5/24
Ответ 5/24
-
Вопрос 279 Вычислить двухкратный интеграл
 Ответ 23/12
Ответ 23/12 -
Вопрос 280 Вычислить двухкратный интеграл
 Ответ 40
Ответ 40 -
Вопрос 286 Найти наибольшую скорость возрастания функции
 в
точке
в
точке
 .
.-
Ответ

-
-
Вопрос 287 Найти градиент функции
 в точке
в точке
 Ответ
Ответ

Дифференциальные уравнения
-
Вопрос 098 Решите уравнение:
 Ответ
Ответ

-
Вопрос 108 Решите уравнение:
 Ответ
Ответ

-
Вопрос 109 Решите уравнение:
 Ответ
Ответ

-
Вопрос 110 Решите уравнение:
 Ответ
Ответ

-
Вопрос 111 Решите уравнение:
 Ответ
Ответ

-
Вопрос 116 Решите уравнение:
 Ответ
Ответ

-
Вопрос 117 Решите уравнение:
 Ответ
Ответ

-
Вопрос 118 Решите уравнение:
 Ответ
Ответ

-
Вопрос 119 Решите уравнение:
 Ответ
Ответ

-
Вопрос 120 Решите уравнение:
 Ответ
Ответ

-
Вопрос 121 Решите уравнение:
 Ответ
Ответ

-
Вопрос 122 Решите уравнение:
 Ответ
Ответ
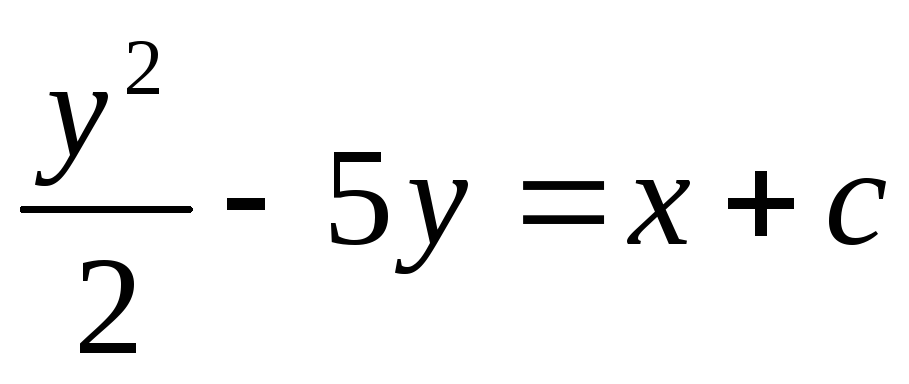
-
Вопрос 123 Решите уравнение:
 Ответ
Ответ

-
Вопрос 124 Решите уравнение:
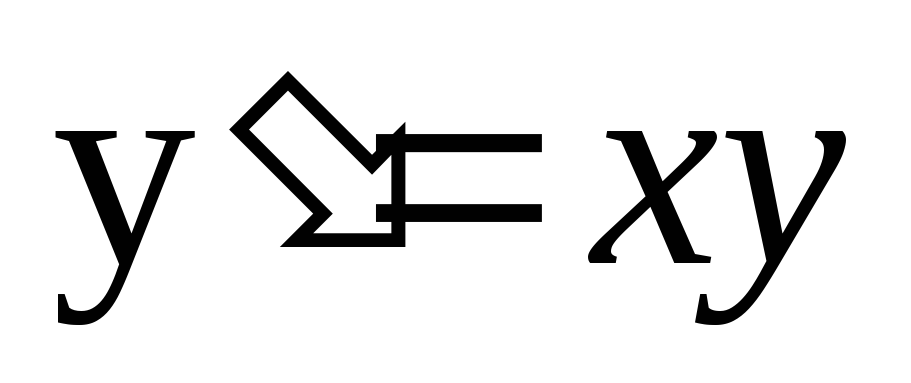 Ответ
Ответ

-
Вопрос 127 Найти общее решение дифференциального уравнения
 Ответ
Ответ

-
Вопрос 128 Найти общее решение дифференциального уравнения
 Ответ
Ответ

-
Вопрос 129 Найти общее решение дифференциального уравнения
 Ответ
Ответ

-
Вопрос 130 Найти общее решение дифференциального уравнения
 Ответ
Ответ

-
Вопрос 131 Найти общее решение дифференциального уравнения
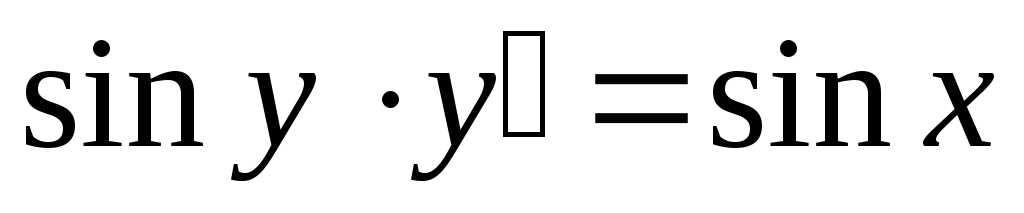 Ответ
Ответ

-
Вопрос 132Найти общее решение дифференциального уравнения
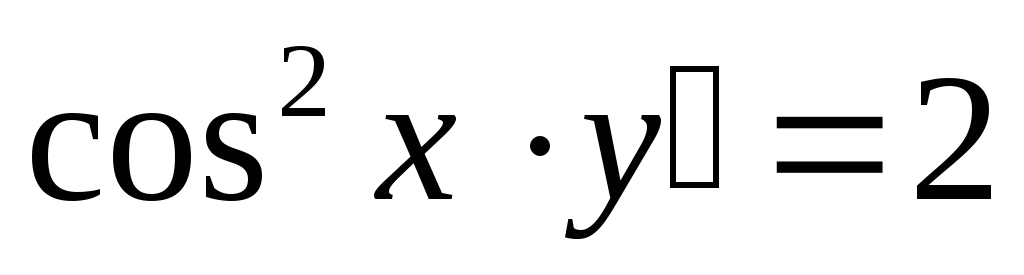 Ответ
Ответ

-
Вопрос 133 Найти общее решение дифференциального уравнения
 Ответ
Ответ
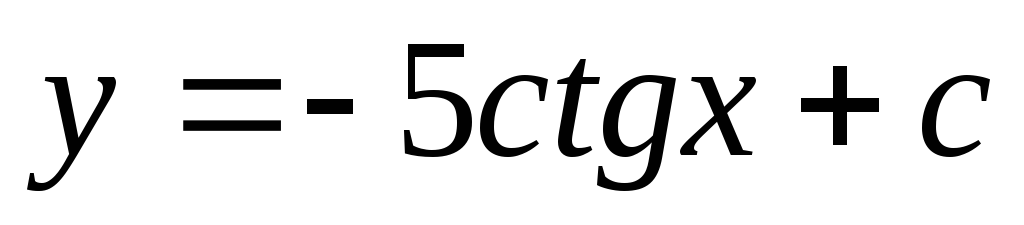
-
Вопрос 239. Общий интеграл или общее решение дифференциального уравнения
 есть функция: Ответ
есть функция: Ответ

-
Вопрос 247 Найти общее решение дифференциального уравнения
 Ответ
Ответ

-
Вопрос 134Найти общее решение дифференциального уравнения
 Ответ
Ответ

-
Вопрос 135Найти общее решение дифференциального уравнения
 Ответ
Ответ

-
Вопрос 097 Решите уравнение:
 Ответ
Ответ
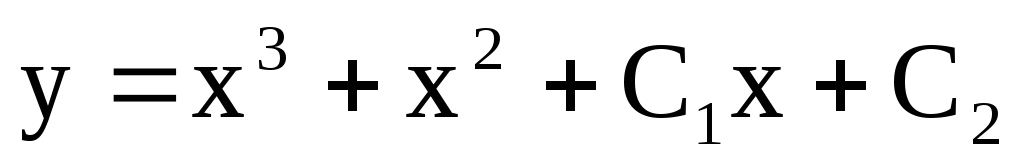
-
Вопрос 099 Решите уравнение:
 Ответ
Ответ

-
Вопрос 100 Решите уравнение:
 ,
если
,
если
 Ответ
Ответ

-
Вопрос 101 Решите уравнение:
 ,
если
,
если
 Ответ
Ответ
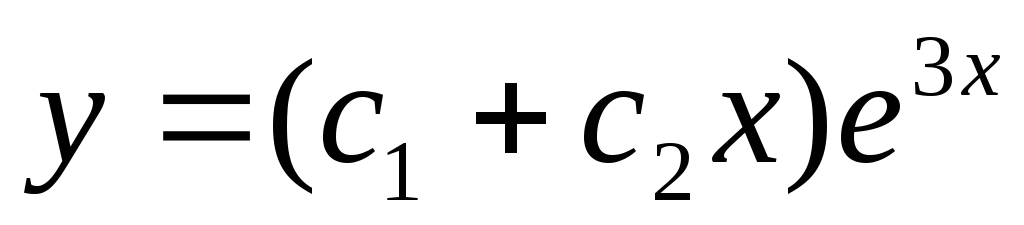
-
Вопрос 112 Решите уравнение:
 ,
если
,
если
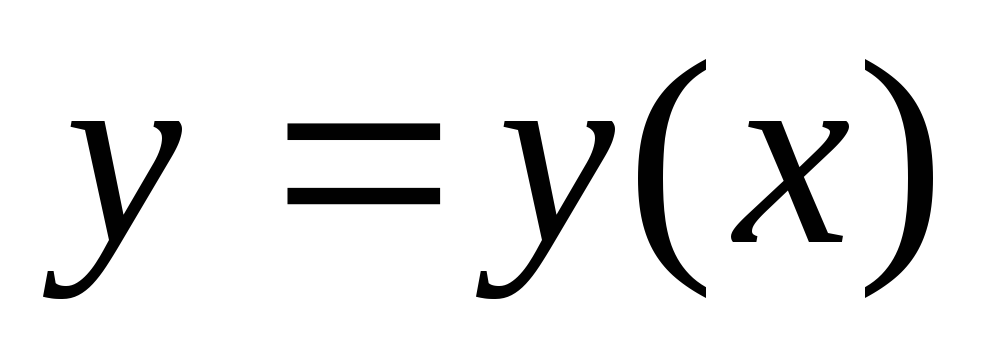 Ответ
Ответ

-
Вопрос 113 Решите уравнение:
 ,
если
,
если
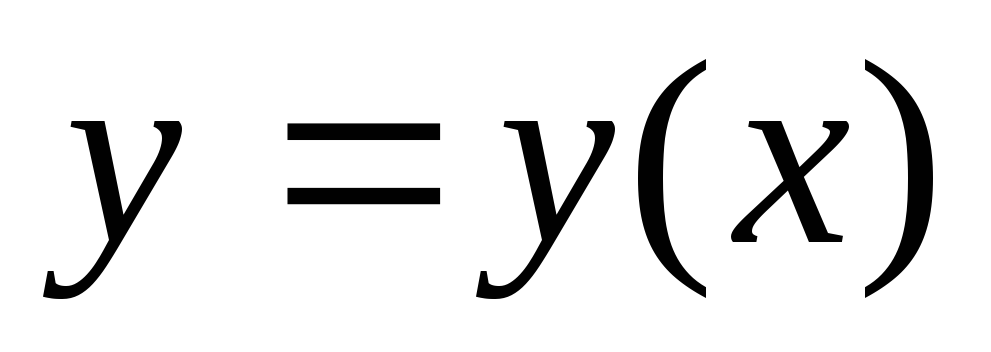 Ответ у=
Ответ у=
-
Вопрос 114 Решите уравнение:
 ,
если
,
если
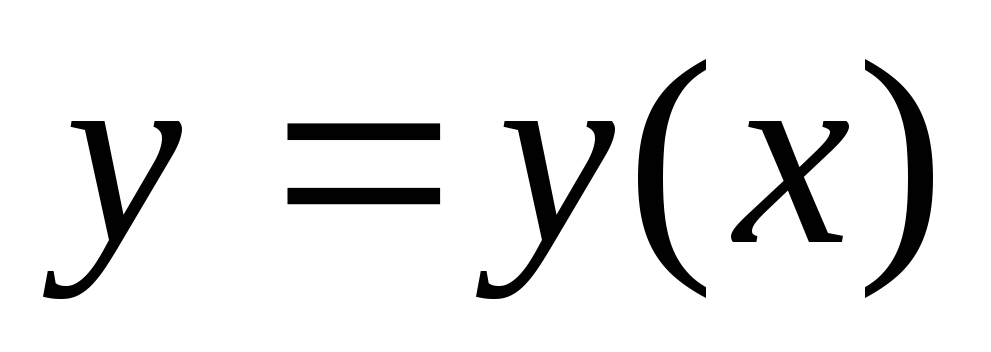 Ответ
Ответ

-
Вопрос 115 Решите уравнение:
 ,
если
,
если
 Ответ
Ответ

-
Вопрос 273 Решите уравнение:
 ,
если
,
если
 Ответ
Ответ
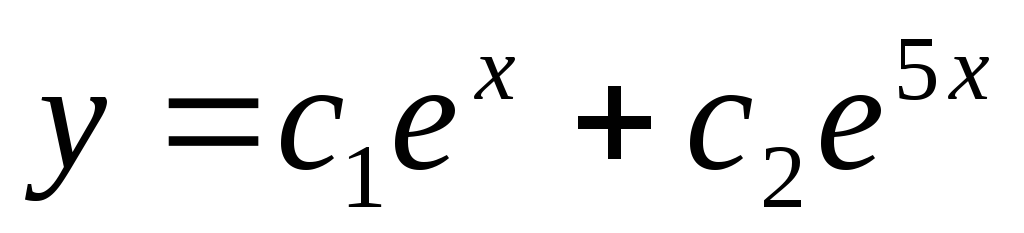
-
Вопрос 303 Решить уравнение
 Ответ
Ответ
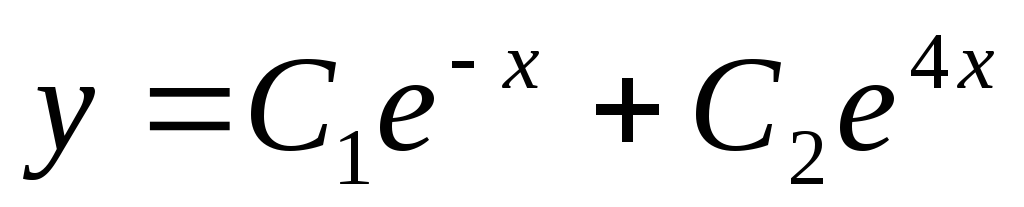
-
Вопрос 304 Решить уравнение
 Ответ
Ответ

-
Вопрос 305 Решить уравнение
 Ответ
Ответ

-
Вопрос 306 Решить уравнение
 Ответ
Ответ

-
Вопрос 307 Решить уравнение
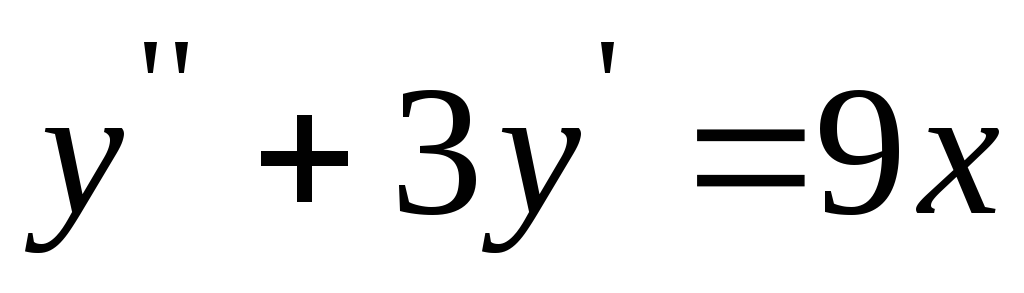 Ответ
Ответ

-
Вопрос 145 Решить уравнение
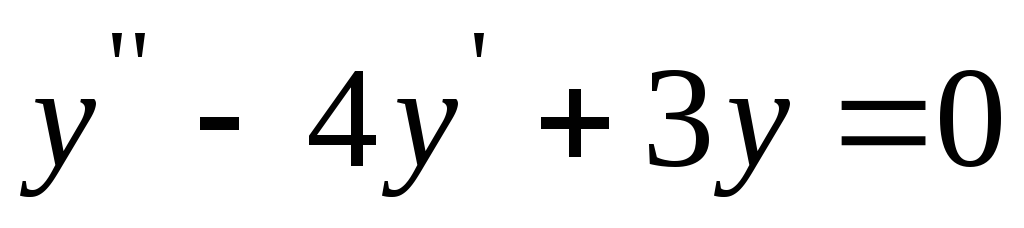 Ответ
Ответ

-
Вопрос 236. Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами
 имеет
вид Ответ
имеет
вид Ответ

-
Вопрос 240. Найти решение дифференциального уравнения y´´-2y´+2y=0 Ответ

-
Вопрос 105 Если
 дифференциальное уравнение
первого порядка, то функция
дифференциальное уравнение
первого порядка, то функция
 называется его .... Ответ
решением
называется его .... Ответ
решением
-
Вопрос 106 В дифференциальном уравнении, кривая заданная уравнением
 определяет … кривую
определяет … кривую
-
Ответ интегральную
-
Вопрос 107 Дифференциальное уравнение удовлетворяющее начальным условиям, называется .... решением
-
Ответ частным
-
Вопрос 136 Найти общее решение дифференциального уравнения
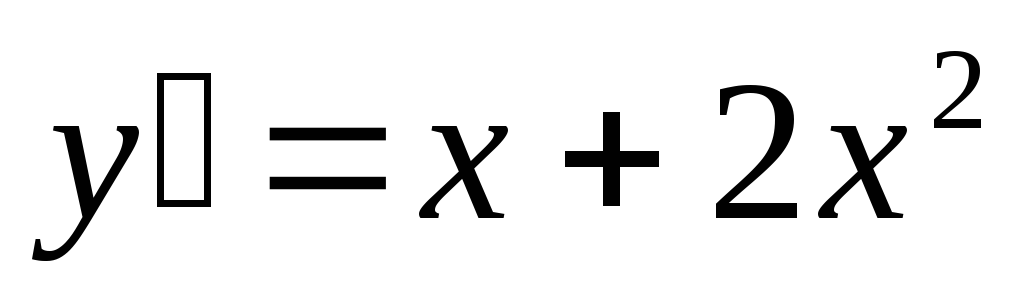 Ответ
Ответ

-
Вопрос 137 Найти общее решение дифференциального уравнения
 Ответ
Ответ

-
Вопрос 238. Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами
 имеет
вид: Ответ
имеет
вид: Ответ

-
Вопрос 138 Найти общее решение дифференциального уравнения
 Ответ
Ответ
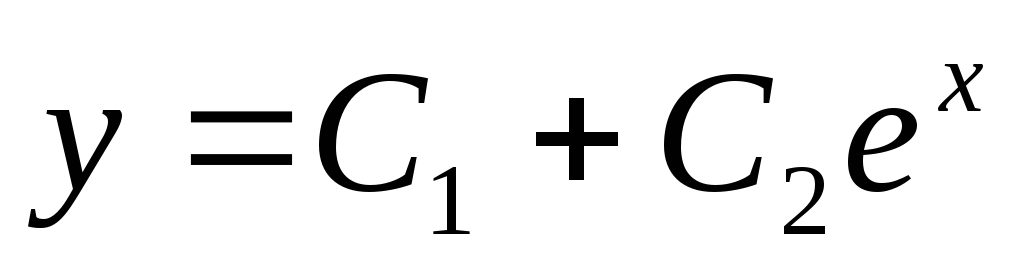
-
Вопрос 200 Какие из следующих дифференциальных уравнений первого порядка являются линейными:



 .
Ответ
.
Ответ

-
Вопрос 201 Уравнение Бернули, это уравнение вида: Ответ

-
Вопрос 202 Какие из следующих дифференциальных уравнений первого порядка являются уравнениями с разделяющими переменными:
 ,
,


 .
Ответ
.
Ответ

-
Вопрос 215 Укажите дифференциальное уравнение n–го порядка: Ответ

-
Вопрос 237. Уравнение
 является дифференциальным уравнением:
является дифференциальным уравнением: -
Ответ в полных дифференциалах.
-
Вопрос 245. Дифференциальным уравнением 1-го порядка называется … Ответ уравнение связывающие независимую переменную, искомую функцию и производную
-
Вопрос 246 Дифференциальное уравнение
 называется однородным, если функция
называется однородным, если функция
 есть
есть
-
Ответ однородная функция нулевого порядка
-
Вопрос 248. Дифференциальным уравнением п-го порядка называется уравнение … Ответ связывающие независимую переменную, искомую функцию и производную п-го порядка
-
Вопрос 250 Дифференциальное уравнение
 называется уравнением в полных
дифференциалах, если
называется уравнением в полных
дифференциалах, если
 и
и
 непрерывные функции, имеющие непрерывные
частные производные 1-го порядка и
удовлетворяющие условию
Ответ
непрерывные функции, имеющие непрерывные
частные производные 1-го порядка и
удовлетворяющие условию
Ответ

-
Вопрос 251 Пусть
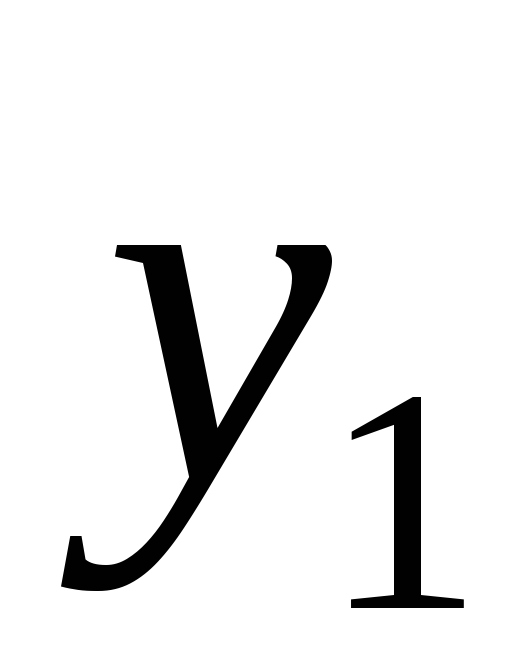 и
и
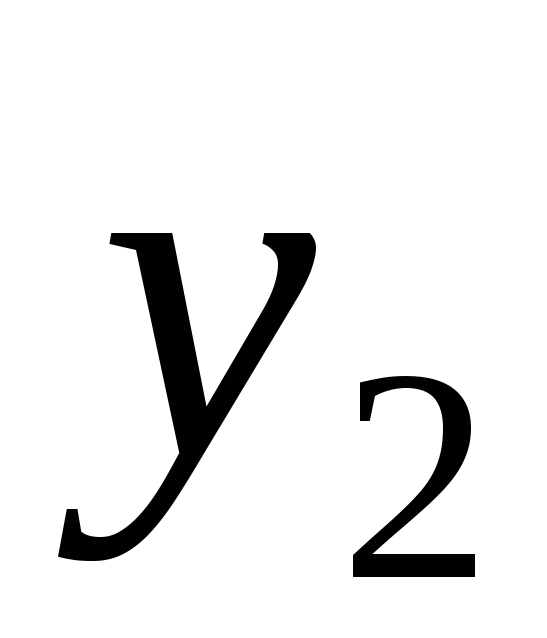 -
решения дифференциального уравнения
-
решения дифференциального уравнения

 ,
в каком из следующих случаев они являются
линейно независимыми:
,
в каком из следующих случаев они являются
линейно независимыми:
-
Ответ

-
Вопрос 253 Линейные неоднородные дифференциальные уравнения, это уравнения Ответ содержащие искомую функцию, производные и правую часть специального вида.
-
Вопрос 268 Какие из следующих формул могут определять общее решение некоторого линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами: Ответ
 .
.
