тест-матем-рус

$$

$

$

$

$$$314.Записать уравнение плоскости, проходящей через начало координат

$$

$

$

$

$$$315. Определить уравнение плоскости, параллельной оси Ох

$$

$

$

$

$$$316. Определить уравнение плоскости, параллельной оси Оу

$$

$

$

$

$$$317. Определить уравнение плоскости в отрезках

$$

$

$

$

$$$318. Уравнение плоскости проходящей через три различные точки, не лежащие на одной прямой:

$$

$

$

$

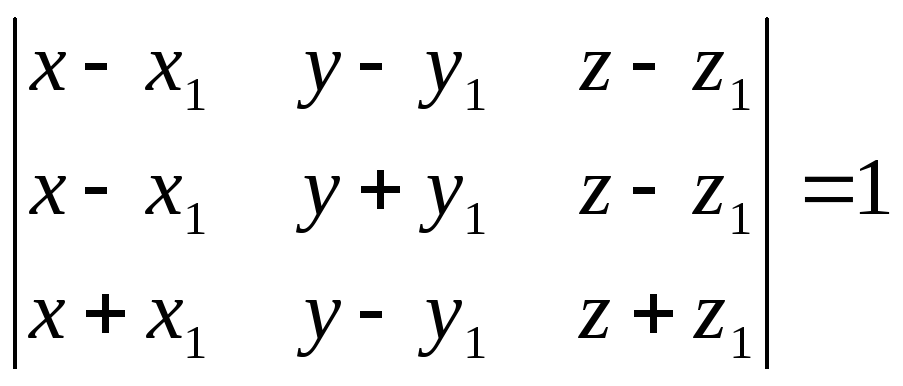
$$$319. Найти производную функции

$$

$

$

$

$$$320. Найти производную функции.

$$

$

$

$

$$321. называется формулой

$$ Ньютона-Лейбница

$ Кронеккера-Капелли

$ интегрированием по частям

$ замены переменной

$$$322. Как называются интегралы с бесконечными пределами :

$$ несобственными интегралами

$ неопределенным интегралом

$ интегральной суммой

$ собственными интегралами

$$$323. Определить уравнение плоскости, параллельной оси Oz

$$

$

$

$

$$$324. Определить уравнение плоскости, параллельной координатной плоскости O_XY.

$$

$

$

$

$$$325. Определить нормальное уравнение плоскости:

$$

$

$

$

$$$326.Расстояние (d) между двумя точками и на плоскости выражается формулой:

$$

$

$

$

$$$327. Определить общее уравнение прямой, на плоскости ОХУ:

$$

$

$

$

$$$328. Прямые вида называются …

$$ директрисами

$ эксцентриситетом

$ фокусом

$ асимптотой

$$$329. Уравнение прямой в отрезках:

$$

$

$

$

$$$330. Пусть задана функция с областью определения . Функция называется нечетной, если выполняется условие:

$$

$

$

$

$$$331. Последовательность называется бесконечно большой если …

$$

$

$

$

$$$332. Найдите интеграл :

$$

$

$

$

$$$333. Определить уравнение координатной плоскости O_XZ

$$

$

$

$

$$$334. Определить уравнение координатной плоскости O_YZ.

$$

$

$

$

$$$335.Найти производную функции

$$

$

$

$

$$$336. Найти производную функции

$$

$

$

$

$$$337 Уравнение линии дано в полярных координатах: . Записать его в декартовых координатах.

$$

$

$

$

$$$338. При каком значении и вектора и коллинеарные.

$$

$

$

$

$$$339. Найти длину дуги полукубической параболы , с началом в точке О(0;0) и с концом в точке В(4; 8)

$$ 64/5

$ 46

$ 3/4

$ 12

$$$340. Найдите параметр параболы

$$ 3

$ 2

$ 6

$ 1

$$$341. Множество всех точек М плоскости, удовлетворяющих условию , где R – радиус, - центр, называется …

$$ окружностью

$ эллипсом

$ гиперболой

$ параболой

$$$342. Уравнение асимптоты гиперболы, имеет вид:

$$

$

$

$

$$$343.Объекты, из которых состоит множество, называются его …

$$ элементами

$ символом

$ промежутками

$ окрестностью

$$$344. Множество, не содержащее ни одного элемента, называется …

$$ пустым

$ нулевым

$ равным

$ единичным

$$$345. Множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В, называется … множеств А и В.

$$ пересечением (произведением)

$ разностью

$ объединением (суммой)

$ делением

$$$346. Множества, элементами которых являются числа, называются …

$$ числовыми

$ нулевыми

$ равными

$ целыми

$$$347. Множество всех точек плоскости Оху, для каждой из которых х является значением аргумента, а у – соответствующим значением функции, называется … функции

$$ графиком

$ аргументом

$ множеством

$ элементом

$$$348. Отрезки, интервалы и полуинтервалы называются … промежутками.

$$ числовыми

$ нулевыми

$ единичными

$ пустыми

$$$349. Произвольный интервал , содержащий точку , называют … точки .

$$ окрестностью

$ пределом

$ объектом

$ аргументом

$$$350. Число а, называется … последовательности , если для любого числа найдётся число , что все числа , у которых , удовлетворяют неравенству .

$$ пределом

$ множеством

$ элементом

$ аргументом

$$$351. Число А, называется пределом … функции при , если .

$$ слева

$ справа

$ окрестности

$ радиуса

$$$352. Число А, называется пределом … функции при , если .

$$ справа

$ точки

$ окрестности

$ слева

$$$353. Пусть и и точка делит отрезок в отношении , то координаты этой точки определяются формулами:

$$

$

$

$

$$$354. Директрисами эллипса, называются прямые вида:

$$

$

$

$

$$$355. Напишите уравнение окружности с центром в точке и радиусом равным 3.

$$ ;

$

$

$

$$$356. Определить вид кривой, заданной уравнением

$$ эллипс

$ гипербола

$ парабола

$ окружность

$$$357. Даны точки и . При каком значении длина вектора АВ равна ?

$$ 6

$ 12

$ –6 и 1

$ -6

$$$358. Найти предел

$$ 4

$ 0

$ 1

$ 2

$$$359. Теорема Ролля. Пусть функция дифференцируема на отрезке и принимает на его концах равные значения:. Тогда такая, что:

$$

$=.

$

$

$$$360. Найти производную функции :

$$

$

$

$