Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Карельская государственная педагогическая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

алгебр.уравн

.pdf

Скачиваний:

Добавлен:

27.02.2016

Размер:

122.09 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10

Учебный центр «Резольвента»

Кандидат физико-математических наук, доцент

С. С. САМАРОВА

РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Учебно-методическое пособие для подготовки к ЕГЭ и ГИА по математике

Пример 1. Решить уравнение

3	−	2x −1	=	2x +1	.	(1)

x + 2 x +1 x2				+ 3x + 2

Решение. Разложим на множители квадратный трехчлен, стоящий в зна-

менателе дроби из правой части уравнения. Для этого сначала нужно найти корни квадратного трехчлена:

x2 + 3x + 2 = 0 Û x = -3 ± 32 - 4 × 2 = -3 ±1 Û x = -2, x = -1.
1,2			2			2		1	2

Следовательно,
	x2 + 3x + 2 = (x +1)(x + 2)
и уравнение (1) принимает форму
3			2x −1			2x +1
		-		=			.		(2)
	x + 2		x +1		(x +1)(x + 2)
ООО «Резольвента», www.resolventa.ru ,						resolventa@list.ru,			(495) 509-28-10 1

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10

Область допустимых значений (ОДЗ) уравнений (1) и (2) имеет вид:

{x ¹ -1, x ¹ -2}.

Умножая обе части уравнения (2) на выражение

(x +1)(x + 2),

и, производя необходимые сокращения, получаем:

3(x +1) - (2x -1)(x + 2) = 2x +1 Û 3x + 3 - (2x2 - x + 4x - 2)= 2x +1 Û Û 3x + 3 - 2x2 + x - 4x + 2 - 2x -1 = 0 Û -2x2 - 2x + 4 = 0 Û

Û x2 + x - 2 = 0 Û x = -1 ± 12 + 4 × 2 =

-1 ± 3 Û x = -2, x =1.

1,2

Корень x1 = −2 не входит в ОДЗ и должен быть отброшен.

Ответ: 1.

Решить уравнение

Пример 2.

x - 3

x2 + 4x + 9

= -2

(3)

x2 + 4x + 9

x - 3

В результате замены переменного

Решение.

x −3

= y,

x2 + 4x + 9

совершенной в уравнении (3), получаем:

y +

= -2 y2 +1 = -2 y Û y2 + 2 y +1 = 0 Û

Û (y +1)2 = 0 Û y = -1.

Следовательно,

x - 3

= -1 x - 3 = -(x2 + 4x + 9)Û x2 + 4x + 9 + x - 3 = 0 Û

x2 + 4x + 9

Û x2 + 5x + 6 = 0 Û x = -3, x = -2.

Проверка показывает, что оба найденных значения удовлетворяют исходному

уравнению (3).

Ответ: −3, − 2.

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10 2

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru,			(495) 509-28-10
		Решить уравнение
	Пример 3.	Решить уравнение

		2x2 + 3x −5 2x2 + 3x + 9 + 3 = 0	(4)

Решение. Уравнение (4) проще всего решить при помощи замены пере-

менного

		2x2 + 3x + 9 = y .							(5)
В этом случае
		2x2 + 3x + 9 = y2
и уравнение (3) принимает вид
y2 - 9 - 5 y + 3 = 0 Û y2 - 5 y - 6 = 0 Û

Û y =	5 ± 52 + 4 × 6			=	5 ± 7	Û y = -1, y			= 6.
Û y =				=		Û y = -1, y		2	= 6.
1,2		2	2				1	2
		2	2

В силу того, что переменная y , определенная по формуле (5), является неотри-

цательным числом, значение y1 = −1 должно быть отброшено. Следовательно,

y = 6 2x2 + 3x + 9 = y2 = 36 Û 2x2 + 3x + 9 - 36 = 0 Û

Û 2x					2 + 3x - 27 = 0 Û x =				-3 ±15			Û x = -		18	= -	9	, x = 3.
Û 2x					2 + 3x - 27 = 0 Û x =							Û x = -			= -		, x = 3.
					1,2					4		1		4	2		2
										4				4	2
		9
Ответ:	-	9		,	3.
Ответ:	-			,	3.
	2
			Решить уравнение
Пример 4.			Решить уравнение
								3
						x	−	3			x		=1				(5)
					1 − x		−						=1				(5)
					1 − x		2				1 − x

Решение. Уравнение (5) проще всего решить при помощи замены пере-

менного

		x		= y .	(6)
				= y .	(6)
	1 − x
В этом случае
		x	= y2
1 − x			= y2
1 − x

иуравнение (5) принимает вид

ООО«Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10 3


ООО «Резольвента», www.resolventa.ru ,										resolventa@list.ru, (495) 509-28-10
	y2 −		3	y −1 = 0 2 y2 −3y − 2 = 0
	y2 −			y −1 = 0 2 y2 −3y − 2 = 0
	2
y =		3 ±					=	3 ± 5	y = −		2
		3 ±			25			3 ± 5			2	= −	1	, y		= 2.
												= −		, y	2	= 2.
1,2	4					4				1	4	2			2
	4					4					4	2

В силу того, что переменная y , определенная по формуле (6), является неотри-

цательным числом, значение y								= −		1	должно быть отброшено. Следовательно,
цательным числом, значение y								= −			должно быть отброшено. Следовательно,
							1		2
									2
	y = 2					x	= y2 = 4		x		= 4 x = 4 − 4x 5x = 4 x =				4	.
	y = 2						= y2 = 4				= 4 x = 4 − 4x 5x = 4 x =					.
1						− x		1	− x				5
			4
	Ответ:		4	.
	Ответ:	5		.
		5
					Решить уравнение
	Пример 5.				Решить уравнение
							(x + 2)2 +						24	=18			(7)
							(x + 2)2 +					x2		=18			(7)
												x2	+ 4x

Решение. Уравнение (7) проще всего решить при помощи замены пере-

менного

x2 + 4x = y .

(8)

В этом случае

(x + 2)2 = x2 + 4x + 4 = y + 4 ,

иуравнение (7) принимает вид

y + 4 + 24 =18 y + 24 −14 = 0 y2 −14 y + 24 = 0

y		y
y	=	14 ±10	y	= 2, y		=12.
y	=		y	= 2, y	2	=12.
1,2	2		1		2
	2

При y1 = 2 из формулы (8) получаем

x2 + 4x = 2 x2 + 4x − 2 = 0 x1,2 = −4 ± 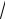24 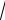= −2 ± 6 2

x1 = −2 − 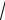6, x2 = −2 + 6.

При y2 =12 из формулы (8) получаем

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10 4

ООО «Резольвента»,

www.resolventa.ru , resolventa@list.ru,

(495) 509-28-10

x2 + 4x =12 x2 + 4x −12 = 0 x =

−4 ±8

x = −6, x = 2.

3,4

− 2 +

−2 −

Ответ:

6; − 6; 2

Решить уравнение

Пример 6.

= x −3

5 − x

(9)

Решение. Заметив, предварительно, что правая часть уравнения (9) должна быть неотрицательным числом и ОДЗ уравнения имеет вид:

x ³ 3,

(10)

возведем обе части уравнения в квадрат:

5 − x = x −3 5 − x = x2 − 6x + 9 x2 −5x + 4 = 0

x1 =1, x2 = 4.

Всилу (10) случай x1 =1 должен быть отброшен. Простая проверка показывает,

что значение x2 = 4 является корнем исходного уравнения.

Ответ: 4 .

Пример 7. Решить уравнение

x + 5	=
		x + 2	(11)

3x −1

Решение. Заметив, предварительно, что оба подкоренных выражения в уравнении (9) должны быть неотрицательными числами, возведем обе части уравнения в квадрат:

x + 5

= x + 2 x + 5 = (x + 2)(3x −1)

x + 2

3x −1

x + 5 = 3x2 + 6x − x − 2 3x2 + 4x − 7 = 0 x = −4 ±10

x = −

, x =1.

1,2

Значение x = −

должно быть отброшено, поскольку в этом случае подкорен-

ное выражение из правой части уравнения (11) отрицательно. Простая провер-

ка показывает, что значение x2 =1 является корнем исходного уравнения.

Ответ: 1.

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10 5

ООО «Резольвента», www.resolventa.ru ,

resolventa@list.ru,

(495) 509-28-10

Решить уравнение

Пример 8.

2x +

7x2

+ x

= 0 .

(12)

x +1

Переписывая уравнение (12) в виде

Решение.

7x2 + x

= −2x ,

(13)

x +1

заметим, что правая часть уравнения (13) должна быть неотрицательной, т.е.

должно выполняться неравенство

-2x ³ 0 Û x £ 0 .	(14)
Также, в силу запрета деления на нуль, должно выполняться соотношение
x ¹ -1.	(15)

Для того, чтобы найти корни уравнения (13), возведем обе его части в квадрат:

	7x2 + x			= 4x2 7x2 + x = 4x2 (x +1) 4x2 (x +1)− 7x2 − x = 0
				= 4x2 7x2 + x = 4x2 (x +1) 4x2 (x +1)− 7x2 − x = 0
		x +1										(				)
		(	)				+				= 0 x	(				)	= 0
x 4x			x +1		− 7x −1	= 0 x 4x2	+	4x − 7x −1			= 0 x		4x2	−3x −1			= 0
x = 0 4x2 −3x −1 = 0 x = 0, x =									3 ± 5	x = 0, x = −					1	, x =1.
x = 0 4x2 −3x −1 = 0 x = 0, x =										x = 0, x = −						, x =1.
						1		2,3	8		1		2	4		3
									8					4

В соответствии с (14) значение x3 =1 должно быть отброшено. Простая провер-

ка показывает, что значения x = 0, x = −						1	являются корнями исходного урав-
ка показывает, что значения x = 0, x = −							являются корнями исходного урав-
1					2	4
						4
нения.
			1
	Ответ:	0; −	1	.
	Ответ:	0; −		.
		4

Пример 9. Решить уравнение

1	-	1			=	2	.	(16)

x - 2			x	3

Решение. В результате замены переменного

= y, y ³ 0,

(17)

совершенной в уравнении (16), получаем:

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10 6

ООО «Резольвента»,

www.resolventa.ru ,

resolventa@list.ru, (495) 509-28-10

−

3y −3(y − 2)− 2 y (y − 2)

= 0 3y −3(y − 2)− 2 y (y − 2)= 0

y − 2 y 3

3y (y − 2)

3y −3y + 6 − 2 y2 + 4 y = 0 −2 y2 + 4 y + 6 = 0 y2 − 2 y −3 = 0

y =

2 ± 4

y = −1, y

= 3.

1,2

В силу (17) значение y1 = −1 должно быть отброшено. Для значения y2 = 3 по-

лучаем:

x = 3, x = 9.

Простая проверка показывает, что найденное значение является корнем исход-

ного уравнения.

Ответ: 9 .

Пример 10. Решить уравнение

4 + x 26 − x2 = x − 2 .

(18)

Решение. Сначала заметим, что правая часть уравнения (18) должна быть неотрицательной, т.е. должно выполняться неравенство

x - 2 ³ 0 Û x ³ 2 .

(19)

Теперь возведем обе части уравнения (18) в квадрат:

4 + x26 − x2 = x − 2 4 + x26 − x2 = (x − 2)2 4 + x26 − x2 = x2 − 4x + 4x26 − x2 = x2 − 4x x26 − x2 − x2 + 4x = 0 x (26 − x2 − x + 4)= 0

x1 = 0 26 − x2 − x + 4 = 0 x1 = 0 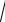26 − x2 = x − 4.

Остается решить уравнение

26 − x2 = x − 4.

(20)

Правая часть уравнения (20) должна быть неотрицательной, т.е. должно выпол-

няться неравенство

x - 4 ³ 0 Û x ³ 4 .

(21)

Возводя обе части уравнения (20) в квадрат, получим:

26 − x2 = x − 4 26 − x2 = x2 −8x +16 2x2 −8x −10 = 0

x2 − 4x −5 = 0 x2 = −1, x3 = 5.

ООО«Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10 7

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10

Итак, мы нашли три значения:

x1 = 0, x2 = −1, x3 = 5.

В силу (19) и (21), значения x1 и x2 должны быть отброшены. Простая проверка показывает, что значение x3 = 5 является корнем исходного уравнения.

Ответ: 5 .

Пример 11. Решить уравнение

3x +10

−

x + 2

= 2. .

(22)

Возводя обе части уравнения (22) в квадрат, получим

Решение.

−

= 2 3x +10 − 2

+ x + 2 = 4

3x +10

x + 2

3x +10

x + 2

4x +8 = 2

2x + 4 =

3x +10

x + 2

3x +10

x + 2.

Теперь возведем в квадрат обе части полученного уравнения:

2x + 4 =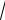3x +10 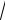x + 2 (2x + 4)2 = (3x +10)(x + 2)

4x2 +16x +16 = 3x2 +10x + 6x + 20 x2 − 4 = 0 x1 = −2, x2 = 2.

Проверка показывает, что оба найденных значения удовлетворяют исходному

уравнению.

Ответ: −2; 2.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Решить уравнения:

		x −1	1			2 + 3x
1.	1 +		+		=		,
		x + 2		x		x (x + 2)

+2t −1 = 4t + 3

2.2 + 2 2t +1 ,t

	2 y +1 y +1				5 y + 4
3.		+		=		,
	y −1		2 y +1		(y −1)(2 y +1)

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10 8

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10

4.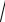12 − 2x + x2 = x + 2 ,

5.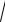−11 +8x − x2 = x −3 ,

		x +10			=						,
6.		x +10							5x − 6
6.									5x − 6
		x +1

7.	x +		x2 +8x							= 0 ,

				x +		3
				x +		3

8.	1	=	2				,
8.	x	=					,
	x		1 − x

9.	2	=	2					,

x 4 − x

10.3x = x3 +8x2 − 6x ,

11.	1 −3x		=	x −	1	,

		3x		3

12. x + 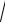x3 + 2x2 −12x = 0 ,

13.3 − 4x = 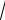8x − 6 ,

14.x2 − 24 − 2 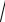x2 − 24 =15 ,

ООО«Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10 9

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-10

15.13 − x2 − 213 − x2 = 3 ,

16.x2 − 21 − x2 − 21 = 2 ,

17.10 − x2 − 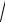10 − x2 = 6 ,

				3
18.				3			+ 2 x +1 = 5 ,
					+1
			x +1		+1
19.	1					−	1			=	1		,
19.						−				=			,
			x −1					x	6
									4
20.		2 − x +							4					= 2 ,

												+ 3
								2 − x				+ 3

21.

2x +

6x2 +1 = x +1,

22.

x −1

−

x +1

x −1 2

= 2 ,

23.

x −1

−

2x +1

x −1

24.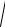4 + x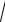9x2 +16 = −x + 2 ,

25.	2	x + 4	−	1 − 2x	=1,

		1 − 2x		x + 4

ООО «Резольвента», www.resolventa.ru , resolventa@list.ru, (495) 509-28-1010

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.02.201695.74 Кб16SPP_SPT_Rumyantseva.doc
#
27.02.201613.86 Mб54stolypin.doc
#
27.02.201650.2 Кб146Vvedenie_2.docx
#
26.11.2019398.34 Кб15_uud.doc
#
26.02.201675.26 Кб56адаптация.doc
#
27.02.2016122.09 Кб24алгебр.уравн.pdf
#
19.12.20183.4 Mб72альбом с методиками.doc
#
27.02.201622 Кб42анализ слова.docx
#
27.02.201622.11 Кб16Анализ стихотворения К. Д. Бальмонта Ветер..docx
#
26.02.201629.7 Кб25Анализ стихотворения Лермонтова М. Парус..doc
#
27.02.2016993.09 Кб33Анна Фрейд Защитные механизмы.rtf