Геометрия теория, 2 семестр / лин 1 пор

Раздел 4. Прямая на плоскости

4.1 Различные виды уравнения прямой

Каждая прямая на плоскости Oxy определяется линейным уравнением первой степени с двумя неизвестными. Обратно: каждое линейное уравнение первого порядка с двумя неизвестными определяет некоторую прямую на плоскости.

Уравнение прямой с угловым коэффициентом имеет вид , (2.1), где k –угловой коэффициент прямой (т.е. тангенс угла , который прямая образует с положительным направлением оси Ox, ), b – ордината точки пересечения прямой с осью Oy.

Общее уравнение прямой: , (2.2), где A, B, C – постоянные коэффициенты, причем А и В одновременно не обращаются в нуль ().

Вектор – называется нормальным вектором прямой или вектором нормали ( перпендикулярен прямой).

Частные случаи этого уравнения:

() – прямая проходит через начало координат;

() – прямая параллельна оси Oy;

() – прямая параллельна оси Ox;

Ax=0 (B=C=0) -прямая совпадает с осью Oy;

By=0 (A=C=0) - прямая совпадает с осью Ox.

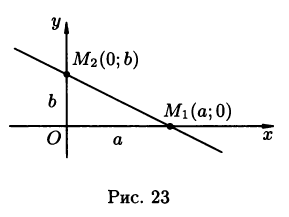
Уравнение прямой в отрезках: +=1, (2.3) где a и b длины отрезков (с учетом знаков) ,отсекаемых прямой на осях Ox и Oy соответственно (рис 23).

4. Уравнение прямой проходящей через данную точку в данном направлении:

y-y₀=k(x-x₀), (2.4)

где k=tg (-угол образуемый прямой с осью Ox); (x₀;y₀)- координаты данной точки. Уравнение (2.4) называют также уравнением пучка прямых с центром в точке (x₀;y₀);уравнение пучка прямых, проходящих через точку пересечения двух прямых A1x+B1y+C1=0 и A2x+B2y+C2=0 имеет вид:

A1x+B1y+C1+ (A2x+B2y+C2)=0,(2.5)

Где -числовой множитель.

5. Уравнение прямой, проходящей через две данные точки М₁(x₁;y₁) и М₂(x₂;y₂),где y₁=/y₂, x₁=/x₂ имеет вид =.

Угловой коэффициент прямой, проходящей через две данные точки определяется по фопмуле

K = .

Если x₁=x₂, то уравнение прямой (2.6) имеет вид x=x₁; если y₁=y₂, то: y=y₁.

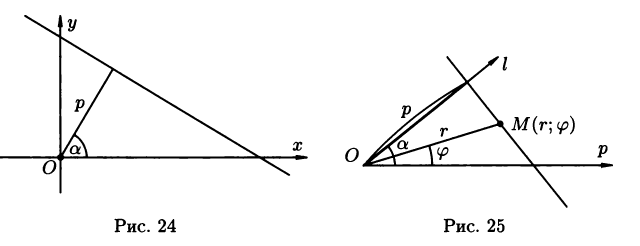
6. Нормальное уравнение прямой.

x+y-p=0, (2.8)

где p- длинна перпендикуляра, опущенного из начала координат на прямую, - угол ,который этот перпендикуляр образует с положительным направлением оси Ох (рис.24)

Общее уравнение прямой (2.2) можно преобразовать в нормальное уравнение (2.8) путём умножения на нормирующий множитель =; знак перед дробью берётся противоположный знаку свободного члена С( в общем уравнении прямой).

7. Уравнение прямой в полярных координатах имеет вид

r=p, (2.9)

r,,,p – изображены на рисунке 25(полярная система координат).

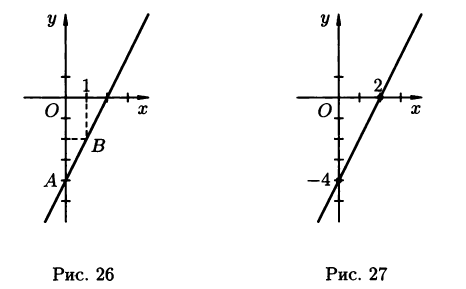
4.2.1. Построить прямую, заданную уравнением 2x-y-4=0.

1). Для построения прямой достаточно знать координаты двух её произвольных точек. Полагая в уравнении прямой, например, x=0, получим y=-4. Имеем одну точку А(0;-4). Полагая x=1, получим y=-2. Отсюда вторая точка В(1;-2).Осталось построить точки А и В и провести через них прямую (рис. 26).

2). Задачу можно решить иначе, используя уравнение прямой в отрезках. Приведём уравнение к виду (2.3). Для этого перенесём свободный член (-4) в правую часть уравнения и обе его части разделим на 4. Получаем 2x-y=4, - = 1, т.е. , - = 1 – уравнение прямой в отрезках на осях. На оси Оx отложим 2 единицы вправо (от начала координат); на оси Оy отложим 4 единицы вниз. Получаем две точки на осях ,через которые проводим прямую (рис.27).

4.2.6.Уравнение прямой 4x-3y+12=0 представить в различных видах ( с угловым коэффициентом, в отрезках, в виде нормального уравнения).

Для получения уравнения прямой с угловым коэффициентом разрешим заданное уравнение относительно y.Получим 3y=4x+12 b и далее y= x+4 – уравнение прямой с угловым коэффициентом; здесь k=, b=4.

Для получения уравнения прямой в отрезках перенесём свободный член C=12 вправо и разделим обе части уравнения на -12. В результате получим , + = 1- уравнение в отрезках на осях; здесь a=-3, b=4.

Приведём исходное уравнение к нормальному виду (2.8).

Для этого умножим обе части уравнения 4x-3y+12=0 на нормирующий множитель= , т.е. = . Перед корнем взят знак «минус», т.к.свободный член (С=12) имеет знак «плюс». Получим - (4x-3y+12)=0, т.е. -x+y-=0; здесь=, sin= (+= + = 1), p=, т.е. расстояние от О(0;0) до прямой равно2,4.

4.2.8. Написать уравнение прямой, проходящей через точки:

А) А(0;2), В(-3;7);

Б) А(2;1), В(4;1);

Решение:

А) Используем уравнение (2.6). Полагая в нём x₁=0, y₁=2, x₂=-3, y₂=7, получим = ,или

=, т.е. -3y+6=5x или 5x+3y-6=0.

Б) Решаем аналогично: =. Так как y₁=y₂, заключаем, что y-1=0, y=1 есть уравнение прямой, проходящей через точки А и В. (Для наглядности построим точки и прямую в системе Oxy- см.рис.28.)

4.2.12 Из пучка прямых определяемых уравнением y+3=k(x-2) выделить ту, которая проходит через точку А(-2;5).

Подставим координаты точки А в уравнение прямой: 5+3=k(-2-2), получим k=8:(-4)=-2. Следовательно, искомое уравнение прямой есть y+3=-2(x-2), т.е. 2x+y-1=0.

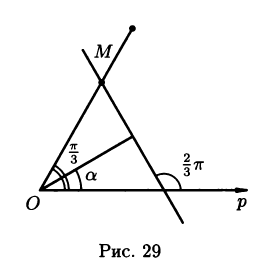
4.2.14. Составить уравнение прямой в полярных координатах, если известно, что она проходит через точку М(2;) и наклонена к полярной оси под углом .

Решение: воспользуемся уравнением(2.9). Очевидно(см.рис.29)  = -( -)= - =. Тогда

p=2 - )=2=2=, т.е. p=. Следовательно, уравнение искомой прямой есть r - )=.

Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, расстояние от данной точки до данной прямой.

Под углом между прямыми в плоскости понимают наименьший (острый) из двух смежных углов, образованными этими прямыми.

Если прямые l₁ и l₂ заданы уравнениями с угловыми коэффициентами y=k₁x+b₁ и y=k₂x+b₂, то угол  между ними вычисляется по формуле:

tg= (2.10)

Условие параллельности прямых l₁ и l₂ имеет вид

k₁=k₂ (2.11)

а условие их перпендикулярности

k₁= (2.12)

(или k₁k₂=-1).

Если прямые l₁ и l₂ заданы общими уравнениями A₁x+B₁y+C₁=0 и A₂x+B₂y+C₂=0,то величина  угла между ними вычисляется по формуле:

tg=, (2.13)

условие их параллельности

= (или A₁B₂-A₂B₁=0, (2.14)

Условие их перпендикулярности

A₁A₂-B₁B₂=0. (2.15)

Для нахождения общих точек прямых l₁ и l₂ необходимо решить систему уравнений

или (2.16)

При этом :

Если  , то имеется единственная точка пересечения прямых;

Если = - прямые l₁ и l₂ не имеют общей точки, т.е. параллельны;

Если == – прямые имеют бесконечное множество общих точек, т.е. совпадают.

_=> Расcтаянием d от точки М₀(x₀;y₀) до прямой Ax+By+C=0 называется длина перпендикуляра, опущенного из этой точки на прямую.

Расстояние d определяется по формуле: d= (2.17)

Расстояние от точки М₀(x₀;y₀) до прямой xcos+ysin-p=0 вычисляется по формуле d= x₀cos+y₀sin-p (2.18)

4.2.52. Найти угол между прямыми:

1) y=2x-3 и y=x+5;

2) 2x-3y+10=0 и 5x-y+4=0;

3) y=x-2 и 8x+6y+5=0;

4) y=5x+1 и y=5x-2.

Решение:

1. Воспользуемся формулой (2.10). Подставляя в неё значения k₁=2 и k₂=, находим tg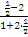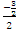=== , =arctg(37);

2. Подставим значения А1=2, В1=-3, А2=5, В2=-1 в формулу (2.13): tg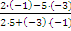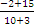===1, =;

3. Здесь k₁=, найдём k₂. Для этого перейдём от 6y=-8x-5к эквивалентному равенству y= -x - . Здесь k₂=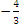. Так как k₁k₂=-,то данные прямые (см.(2.12)) перпендикулярны. (По формуле (2.10) получаем tg== =, =.)

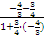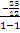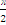4. K₁=5,k₂=5, tg=0, =0.

4.2.57.Через точку пересечения прямых 3x-2y+5=0, x+2y-9=0проведена прямая, параллельная прямой 2x+y+6=0. Составить её уравнение.

Решение: найдём сначала точку М пересечения данных прямых. Для этого решим систему уравнений:

Отсюда 4x=4. И далее, x=1, y=4, т.е. М(1;4). Угловой коэффициент прямой 2x+y-6=0 есть k₁=-2. Следовательно, угловой коэффициент kпрямой параллельной данной, есть k=-2 (см.(2.11)). По направлению прямой (k=-2) и точке М(1;4), ей принадлежащей, запишем уравнение искомой прямой: y—2(x-1), т.е.2x+y-6=0.

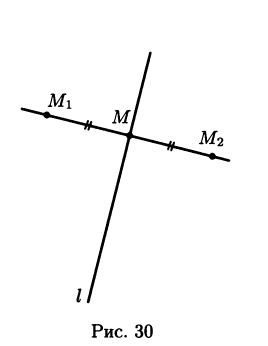
4.2.62. Найти координаты точки М_2, симметричной точке М₁(-3;4) относительно прямой 4x-y-1=0.

Решение: точки М₁ и М₂ лежат на прямой М₁М₂, перпендикулярной прямой 4x-y-1=0, и одинаково удалены от (см.рис.30, прямая l). Найдём уравнение прямой М₁М₂. Так как угловой коэффициент k₁ данной прямой равен 4,то угловой коэффициент k прямой М₁М₂ определяется равенствами k=-= - . Поэтому уравнение прямой М₁М₂ есть y-4=-(x+3),т.е. x+4y-13=0. Найдём координаты точки М- точка пересечения прямой М₁М₂ и данной прямой:

Отсюда x=1, y=3, т.е. М(1;3). Точка М(1;3) делит отрезок М₁М₂ пополам. Из соотношений 1= и 3= находим координаты x и y искомой точки М₂ : x=5, y=2 и М₂(5;2).

4.2.67. Написать уравнение прямой l₂, проходящей через точку А(0;2) под углом к прямой l₁:x-2y+3=0.

Решение: угловой коэффициент прямой l₂ равен , т.е. k₁=. Обозначим через k угловой коэффициент прямой l₂. Тогда по формуле (2.10) имеем tg=1=. Из этого уравнения находим k2=3 и k3=-. Задача имеет два решения. Для каждого случая напишем уравнения прямой, проходящей через точку А в заданном уравнении: y-2=3(x-0) и y-2= - (x-0), т.е. 3x-y+2=0 и x+3y-6=0.

4.2.68. Найти расстояние между параллельными прямыми 3x+4y-20=0 и 6x+8y+5=0.

Решение: возьмём на первой прямой произвольную точку А. Пусть, например,x=0, тогда y=5, т.е. А(0;5). По формуле (2.17) находим расстояние d от точки А до второй прямой:

D===4,5.