
Геометрия теория, 2 семестр / Векторы 2
.docРаздел 3. Векторная алгебра в координатной плоскости
3.1 Основные векторы

Три
взаимно перпендикулярные оси ОХ,
OY
и OZ
образуют прямоугольную систему координат
(раздел 2). Отложив на этих осях в
положительном направлении отрезки ОА,
ОВ
и ОС,
равные единице масштаба, получим три
вектора:
![]() ,
,
![]() и
и
![]() .
Они называются основными
векторами (ортами)
и обозначаются соответственно
.
Они называются основными
векторами (ортами)
и обозначаются соответственно
![]() ,
,
![]() и
и
![]() .
.
3.2 Координаты вектора на плоскости
Если
![]() ,
,
![]() – орты координатных осей прямоугольной
системы координат Оху,
то любой вектор
– орты координатных осей прямоугольной
системы координат Оху,
то любой вектор
![]() единственным образом можно представить
в виде их суммы (линейной комбинации) с
коэффициентами aх
и aу:
единственным образом можно представить
в виде их суммы (линейной комбинации) с
коэффициентами aх
и aу:
![]() .
Коэффициенты ах,
ау
линейной комбинации называют координатами
вектора
.
Коэффициенты ах,
ау
линейной комбинации называют координатами
вектора
![]() в базисе
в базисе
![]() ,
,
![]() .
Координаты ах,
ау
вектора
.
Координаты ах,
ау
вектора
![]() – это его проекции на соответствующие
координатные оси. Вектор
– это его проекции на соответствующие
координатные оси. Вектор
![]() с координатами ах,
ay
записывают в виде
с координатами ах,
ay
записывают в виде
![]() .
Длина вектора
.
Длина вектора
![]() определяется по формуле
определяется по формуле
![]() .
.
Вектор
![]() образует с координатными осями Ох
и Оу
углы α и β соответственно. Направление
вектора
образует с координатными осями Ох
и Оу
углы α и β соответственно. Направление
вектора
![]() определяется с помощью направляющих
косинусов: cosα,
cosβ
для которых справедливы равенства
определяется с помощью направляющих
косинусов: cosα,
cosβ
для которых справедливы равенства
![]() ,
,
![]() .
.
Пусть
даны два вектора
![]() и
и
![]() .
Тогда:
.
Тогда:
-
векторы
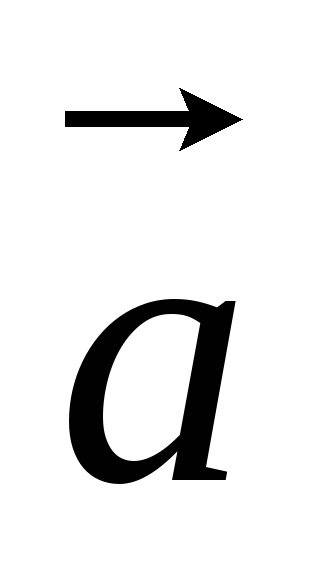 и
и
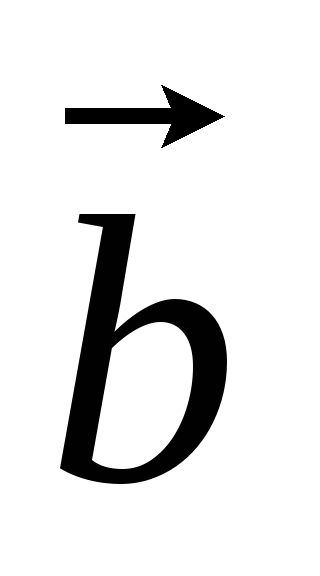 равны тогда и только тогда, когда равны
их соответствующие координаты, т. е.
равны тогда и только тогда, когда равны
их соответствующие координаты, т. е.
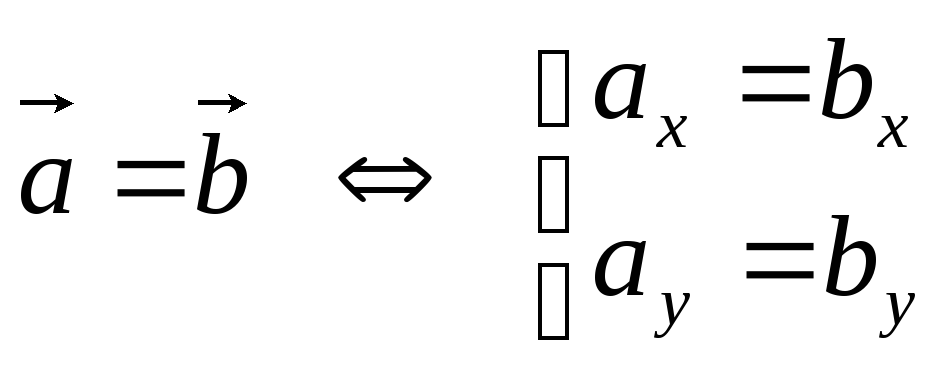 .
. -
векторы
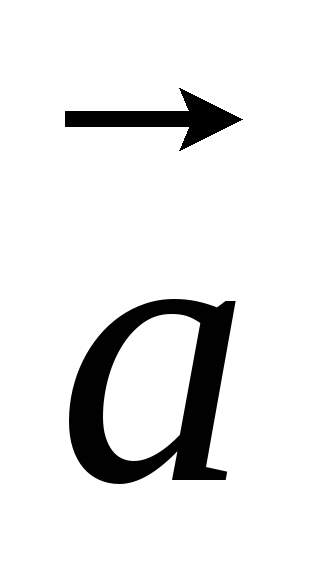 и
и
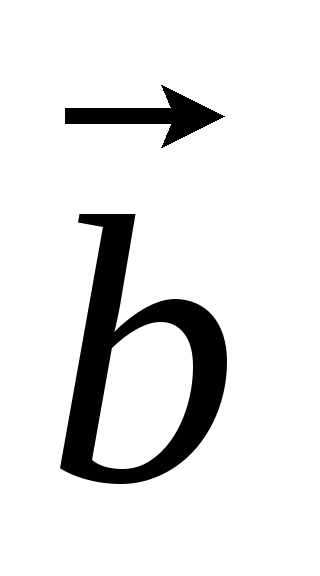 коллинеарны тогда и только тогда, когда
их соответствующие координаты
пропорциональны, т. е.:
коллинеарны тогда и только тогда, когда
их соответствующие координаты
пропорциональны, т. е.:
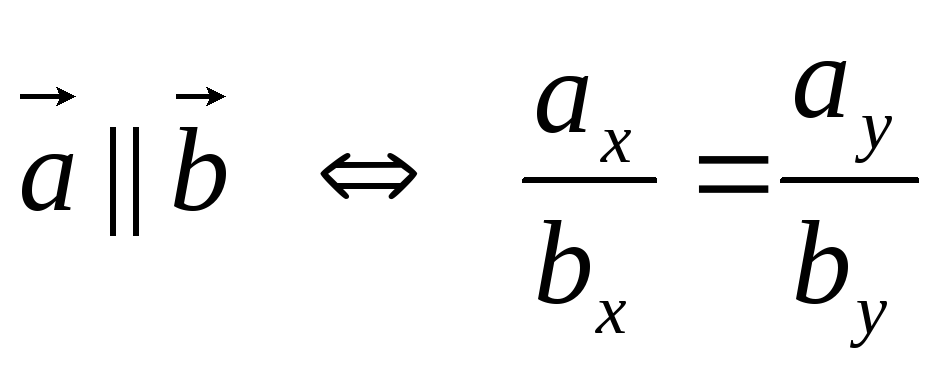 .
. -
При сложении векторов их одноименные координаты складываются, при вычитании – вычитаются, при умножении вектора на число – умножаются на это число:
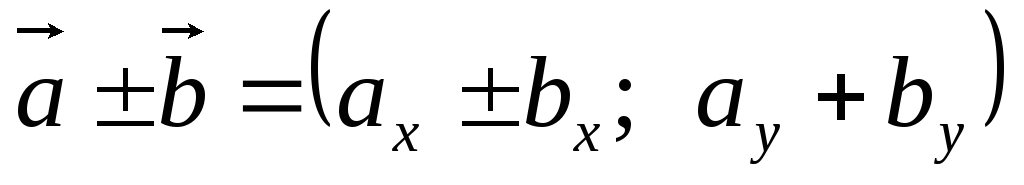 ;
;
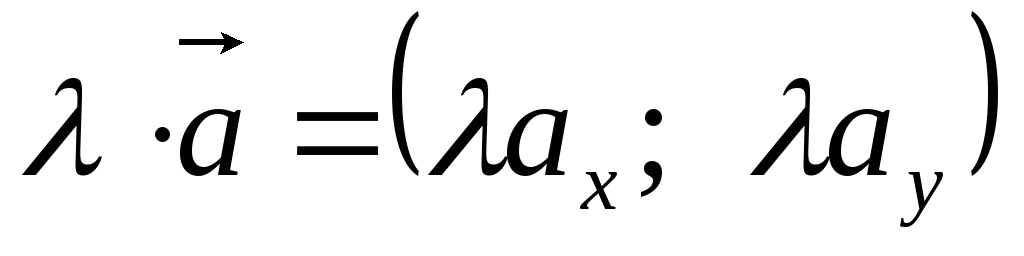 .
.
Вектор
![]() ,
соединяющий начало координат с
произвольной точкой
,
соединяющий начало координат с
произвольной точкой
![]() называется радиус-вектором точки М.
Координаты точки – это координаты ее
радиус-вектора
называется радиус-вектором точки М.
Координаты точки – это координаты ее
радиус-вектора
![]() или
или
![]() .
Если вектор
.
Если вектор
![]() задан точками
задан точками
![]() и
и
![]() ,
то его координаты ах,
аy
вычисляются по формулам
,
то его координаты ах,
аy
вычисляются по формулам
![]() ,
,
![]() :
:
![]() .
.
Если
векторы
![]() и
и
![]() заданы своими координатами
заданы своими координатами
![]() и
и
![]() то их скалярное произведение находится
по формуле:
то их скалярное произведение находится
по формуле:
![]() .
.
3.3 Координаты вектора в пространстве
Если
![]() ,
,
![]() и
и
![]() – орты координатных осей прямоугольной
системы координат Oху,
то любой вектор
– орты координатных осей прямоугольной
системы координат Oху,
то любой вектор
![]() единственным образом можно представить
в виде их суммы (линейной комбинации) с
коэффициентами aх
и aу:
единственным образом можно представить
в виде их суммы (линейной комбинации) с
коэффициентами aх
и aу:
![]() .
Коэффициенты ах,
ау,
аz
линейной комбинации называют координатами
вектора
.
Коэффициенты ах,
ау,
аz
линейной комбинации называют координатами
вектора
![]() в базисе
в базисе
![]() ,
,
![]() и
и
![]() .
Координаты ах,
ау,
аz
вектора
.
Координаты ах,
ау,
аz
вектора
![]() – это его проекции на соответствующие
координатные оси. Вектор
– это его проекции на соответствующие
координатные оси. Вектор
![]() с координатами ах,
ау,
аz
записывают в виде
с координатами ах,
ау,
аz
записывают в виде
![]() .
Длина вектора
.
Длина вектора
![]() определяется по формуле:
определяется по формуле:
![]() (1.1).
(1.1).
Вектор
![]() образует с координатными осями Ох,
Оу
и Oz
углы α, β и γ соответственно. Направление
вектора
образует с координатными осями Ох,
Оу
и Oz
углы α, β и γ соответственно. Направление
вектора
![]() определяется с помощью направляющих
косинусов: cosα,
cosβ
и cosγ
для которых справедливы равенства:
определяется с помощью направляющих
косинусов: cosα,
cosβ
и cosγ
для которых справедливы равенства:
![]() ,
,
![]() ,
,
![]() (1.2).
(1.2).
Пусть
даны два вектора
![]() ,
,
![]() .
Тогда:
.
Тогда:
-
векторы
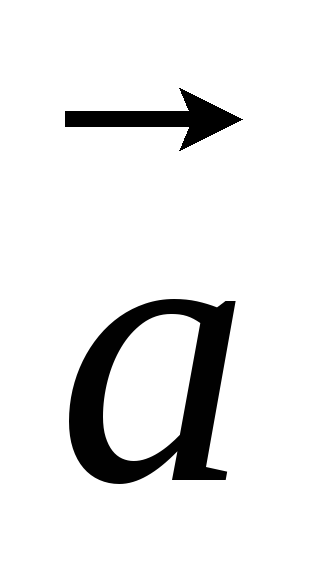 и
и
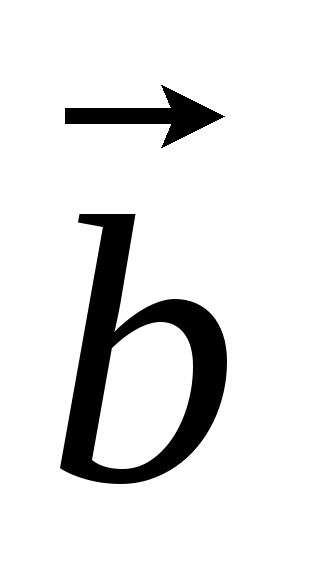 равны тогда и только тогда, когда равны
их соответствующие координаты, т. е.
равны тогда и только тогда, когда равны
их соответствующие координаты, т. е.
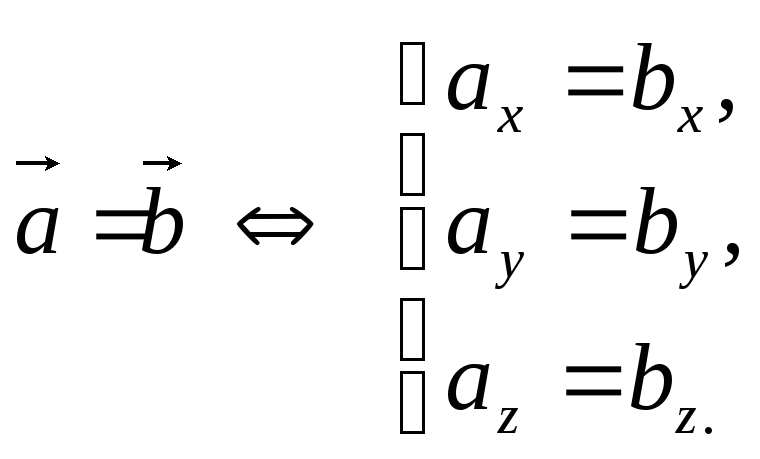
-
векторы
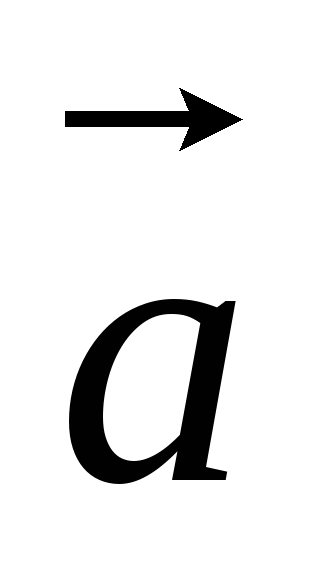 и
и
 коллинеарны тогда и только тогда, когда
их соответствующие координаты
пропорциональны, т. е.
коллинеарны тогда и только тогда, когда
их соответствующие координаты
пропорциональны, т. е.
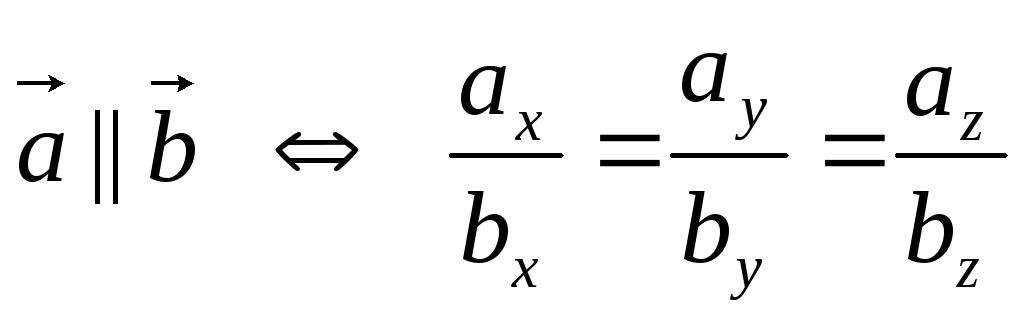 (1.3)
(1.3)
При сложении векторов их одноименные координаты складываются, при вычитании – вычитаются, при умножении вектора на число – умножаются на это число:
![]()
![]()
Вектор
![]() ,
соединяющий начало координат с
произвольной точкой
,
соединяющий начало координат с
произвольной точкой
![]() называется радиус-вектором
точки М.
Координаты точки – это координаты ее
радиус-вектора
называется радиус-вектором
точки М.
Координаты точки – это координаты ее
радиус-вектора
![]() или
или
![]() .
.
Если
вектор
![]() задан точками
задан точками
![]() и
и
![]() ,
то его координаты ах,
аy,
az
вычисляются по формулам:
,
то его координаты ах,
аy,
az
вычисляются по формулам:
![]() ,
,
![]() ,
,
![]() :
:
![]() (1.4).
(1.4).
Пример
1:
Даны три последовательные вершины
параллелограмма:
![]() ,
,
![]() ,
,
![]() .
Найти его четвертую вершину D.
.
Найти его четвертую вершину D.
Решение:
Обозначим
координаты вершины D
через х,
y,
z,
т. е.
![]() .
Так как ABCD
– параллелограмм, то имеем:
.
Так как ABCD
– параллелограмм, то имеем:
![]() .
Находим координаты векторов
.
Находим координаты векторов
![]() и
и
![]() :
:
![]() ,т.е.
,т.е.
![]() ;
;
![]() .
Из равенства векторов
.
Из равенства векторов
![]() и
и
![]() следует, что
следует, что
![]() ,
,
![]() ,
,
![]() .
Отсюда находим:
.
Отсюда находим:
![]() x,
x,
![]() ,
,
![]() .
Итак,
.
Итак,
![]() .
.
Пример
2: Найти
координаты вектора
![]() ,
если известно, что он направлен в
противоположную сторону к вектору
,
если известно, что он направлен в
противоположную сторону к вектору
![]() ,
и его модуль равен 5.
,
и его модуль равен 5.
Решение:
Можно
записать, что
![]() .
Так как вектор
.
Так как вектор
![]() направлен в противоположную сторону к
вектору
направлен в противоположную сторону к
вектору
![]() ,
то
,
то
![]() .
Найдем орт
.
Найдем орт
![]() .
Из равенства
.
Из равенства
![]() находим
находим
![]() .
Но
.
Но
![]() .
Значит,
.
Значит,
![]() .
.
Следовательно,
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
.
Пример
3: Вектор
![]() составляет с осями Ох
и Оу
углы α
= 60° и β
= 120°. Найти его координаты, если
составляет с осями Ох
и Оу
углы α
= 60° и β
= 120°. Найти его координаты, если
![]() .
.
Решение:
Пусть
х,
у,
z
– координаты вектора
![]() ,
то есть
,
то есть
![]() .
Координаты вектора
.
Координаты вектора
![]() найдем из соотношений
найдем из соотношений
![]() ,
,
![]() ,
,
![]() .
Предварительно найдем
.
Предварительно найдем
![]() .
Так как, то
.
Так как, то
![]() ,
то есть
,
то есть
![]() .
Отсюда находим, что
.
Отсюда находим, что
![]() или
или
![]() .
Условию задачи удовлетворяют два вектора
.
Условию задачи удовлетворяют два вектора
![]() и
и
![]() :
:
![]() с направляющими косинусами
с направляющими косинусами
![]() ,
,
![]() ,
,
![]() и
и
![]() с направляющими косинусами
с направляющими косинусами
![]() ,
,
![]() ,
,
![]() .
Имеем:
.
Имеем:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Отсюда находим:
.
Отсюда находим:
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
,
![]() ,
,
![]() .
То есть
.
То есть
![]() и
и
![]() .
.
Пример
4: При
каких значениях α
и β
векторы
![]() и
и
![]() коллинеарны?
коллинеарны?
Решение:
Так
как
![]() ,
то
,
то
![]() (см. условие (1.3)). Отсюда находим, что
(см. условие (1.3)). Отсюда находим, что
![]() ,
,
![]() .
.
Пример
5: Разложить
вектор
![]() по векторам
по векторам
![]() и
и
![]() .
.
Решение:
Требуется
представить вектор
![]() в виде
в виде
![]() ,
где
,
где
![]() и
и
![]() – числа. Найдем их, используя определение
равенства векторов. Имеем:
– числа. Найдем их, используя определение
равенства векторов. Имеем:
![]() ,
,
![]() ,
,
![]() и равенство
и равенство
![]() ,
то есть
,
то есть
![]() .
Отсюда следует, что
.
Отсюда следует, что
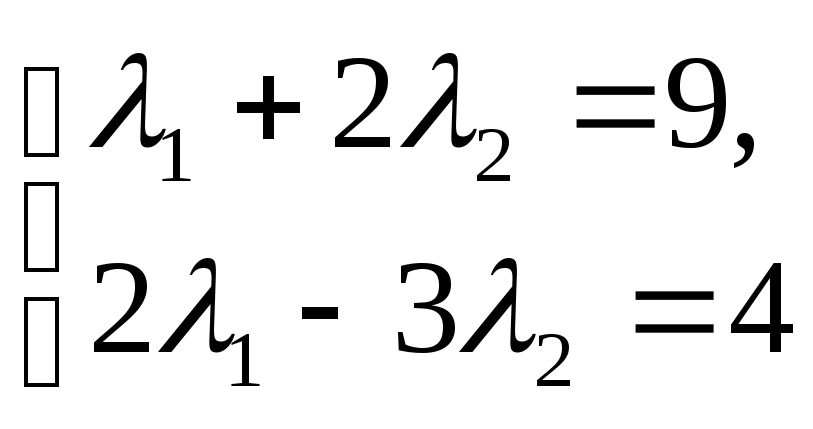 ,
то есть
,
то есть
![]() ,
,
![]() ,
следовательно,
,
следовательно,
![]() .
.
3.4 Векторное произведение векторов
Если
векторы
![]() и
и
![]() заданы своими координатами
заданы своими координатами
![]() ,
,
![]() ,
то
,
то
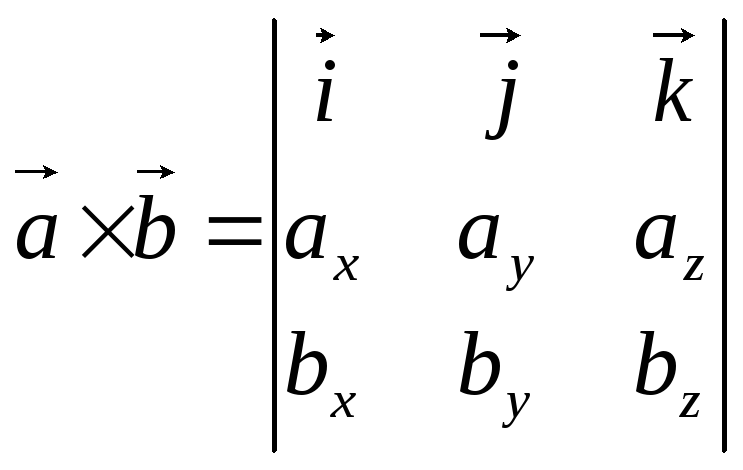 ,
или
,
или
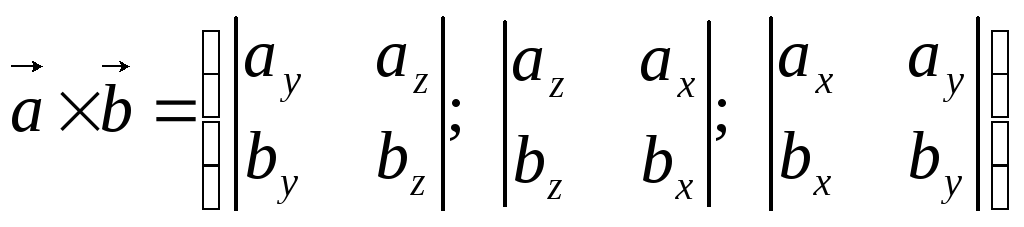 (3.2).
(3.2).
Для
вычисления площади параллелограмма,
построенного на векторах
![]() и
и
![]() применяется формула
применяется формула
![]() (3.3).
(3.3).
Векторное
произведение может быть выражено
формулой
![]() (3.4), где
(3.4), где
![]() – орт направления
– орт направления
![]() .
.
Пример
6: Найти
площадь треугольника с вершинами
![]() ,
,
![]() ,
,
![]() .
.
Решение:
Площадь
S
треугольника АВС
равна половине площади параллелограмма,
построенного на векторах
![]() и
и
![]() ,
то есть
,
то есть
![]() .
Имеем:
.
Имеем:
![]() ,
,
![]() .
Тогда по формуле (3.2)
.
Тогда по формуле (3.2)
![]() ,
то есть
,
то есть
![]() .
Следовательно,
.
Следовательно,
![]() .
.
3.5 Смешанное произведение векторов
Смешанным
произведением
трех векторов
![]() ,
,
![]() и
и
![]() называется число, равное скалярному
произведению вектора
называется число, равное скалярному
произведению вектора
![]() на вектор
на вектор
![]() .
.
Обозначение:
![]() .
.
Таким
образом:
![]() .
.
Геометрически
смешанное произведение интерпретируется
как число, равное объему параллелепипеда,
построенного на векторах
![]() ,
,
![]() и
и
![]() как на ребрах. Смешанное произведение
векторов
как на ребрах. Смешанное произведение
векторов
![]() ,
,
![]() и
и
![]() положительно, если данные векторы
образуют правую тройку, и отрицательно
– если левую.
положительно, если данные векторы
образуют правую тройку, и отрицательно
– если левую.
Свойства смешанного произведения:
-
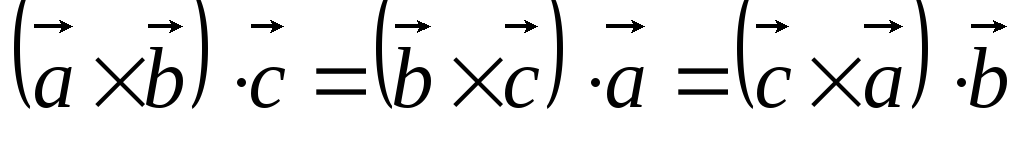 ,
т. е. смешанное произведение не меняется
при циклической перестановке векторов;
,
т. е. смешанное произведение не меняется
при циклической перестановке векторов; -
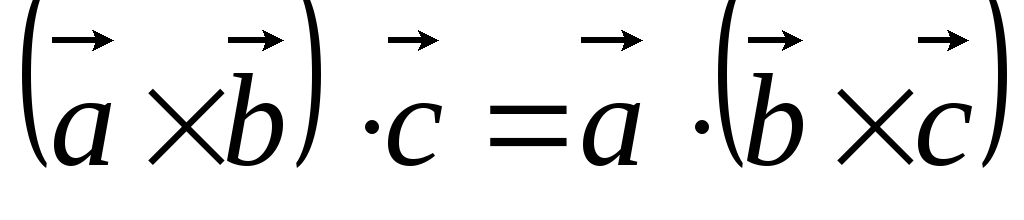 ,
т. е. смешанное произведение не меняется
при перестановке знаков векторного и
скалярного умножения;
,
т. е. смешанное произведение не меняется
при перестановке знаков векторного и
скалярного умножения; -
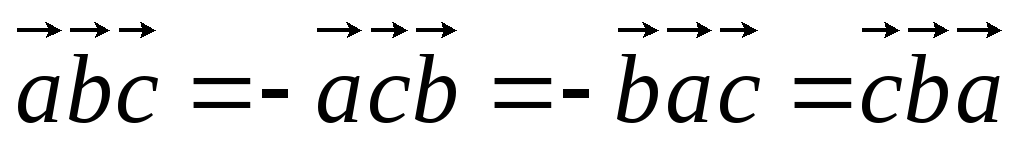 т.е.
смешанное произведение меняет знак на
противоположный при перемене мест
любых двух векторов-сомножителей;
т.е.
смешанное произведение меняет знак на
противоположный при перемене мест
любых двух векторов-сомножителей; -
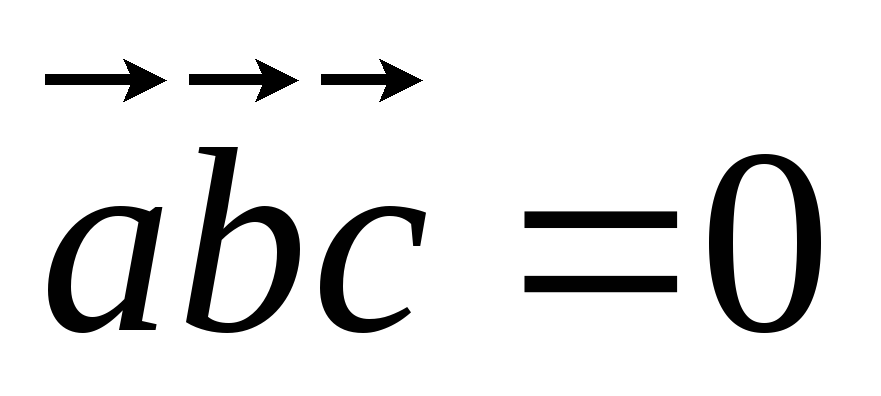 ,
если
,
если
 ,
,
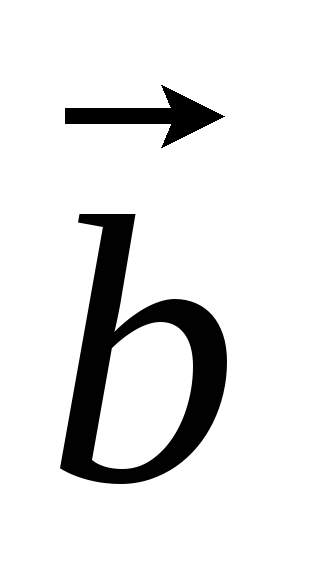 и
и
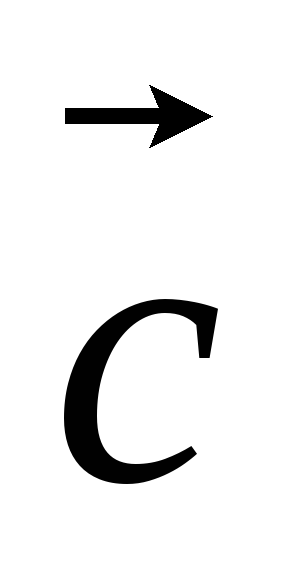 компланарны (в частности, если любые
два из перемножаемых вектора коллинеарны).
компланарны (в частности, если любые
два из перемножаемых вектора коллинеарны).
Если
векторы
![]() ,
,
![]() и
и
![]() заданы своими координатами
заданы своими координатами
![]() ,
,
![]() ,
,
![]() то
то
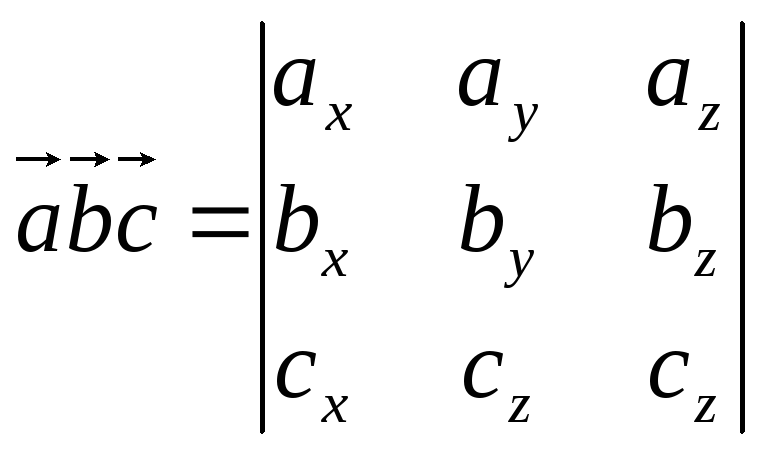 (4.1).
(4.1).
Если
![]() ,
то
,
то
![]() ,
,
![]()
![]() – правая тройка;
– правая тройка;
![]() – левая.
– левая.
Объем
V1
параллелепипеда, построенного на
векторах
![]() ,
,
![]() и
и
![]() ,
и объем V2,
построенной на них треугольной пирамиды,
находятся по формулам
,
и объем V2,
построенной на них треугольной пирамиды,
находятся по формулам
![]() , (4.2)
, (4.2)
![]() . (4.3)
. (4.3)
Пример
7: Доказать,
что четыре точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() лежат в одной плоскости.
лежат в одной плоскости.
Решение:
Достаточно
показать, что три вектора
![]() ,
,
![]() ,
,
![]() ,
имеющие начало в одной из данных точек,
лежат в одной плоскости (то есть
компланарны). Находим координаты векторов
,
имеющие начало в одной из данных точек,
лежат в одной плоскости (то есть
компланарны). Находим координаты векторов
![]() ,
,
![]() ,
,
![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Проверяем условие компланарности векторов (свойство 4 смешанного произведения векторов):
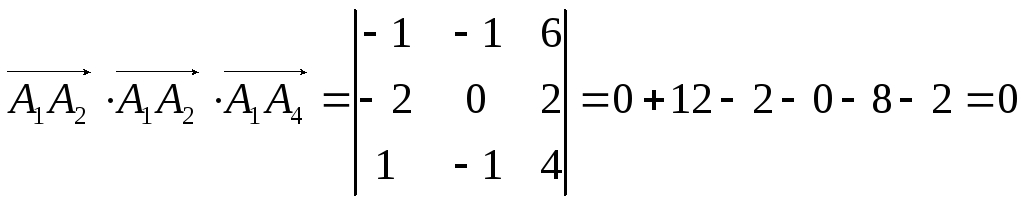 .
.
Следовательно,
векторы
![]() ,
,
![]() и
и
![]() компланарны, а значит, точки
компланарны, а значит, точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() лежат в одной плоскости.
лежат в одной плоскости.
Вопросы для контроля
-
Дайте понятие основных векторов (ортов).
-
Линейная комбинация вектора на плоскости и в пространстве. Координаты вектора на плоскости и в пространстве.
-
Формулы для нахождения длины вектора, заданного своими координатами на плоскости и в пространстве.
-
Условия равенства и коллинеарности векторов на плоскости и в пространстве.
-
Операции над векторами, заданными своими координатами на плоскости и в пространстве (сложение, вычитание, умножение на число, скалярное произведение).
-
Направление вектора на плоскости и в пространстве.
-
Радиус-вектор точки на плоскости и в пространстве.
-
Координаты вектора, заданного координатами его концов на плоскости и в пространстве.
-
Векторное произведение векторов, заданных своими координатами. Свойства векторного произведения.
-
Смешанное произведение векторов. Свойства смешанного произведения.
-
Формула для нахождения смешанного произведения векторов, заданных своими координатами. Применение смешанного произведения векторов для нахождения объема параллелепипеда и треугольной пирамиды.
-
Условие компланарности векторов.
