
прямоугольная система координат
.pdf

Прямоугольную (Декартововую) систему координат на плоскости
в XIX в. ввёл французский математик
Рене Декарт

Прямоугольную систему координат в пространстве
ввёл швейцарский, немецкий, российский математик
Леонард Эйлер
в XVIIIв.
Вопросы:
1. Сколькими координатами может быть
задана точка на прямой? |
Одной. |
|
2. Сколькими координатами может быть задана точка в координатной плоскости?
Вопрос урока. |
Двумя. |
|
может быть
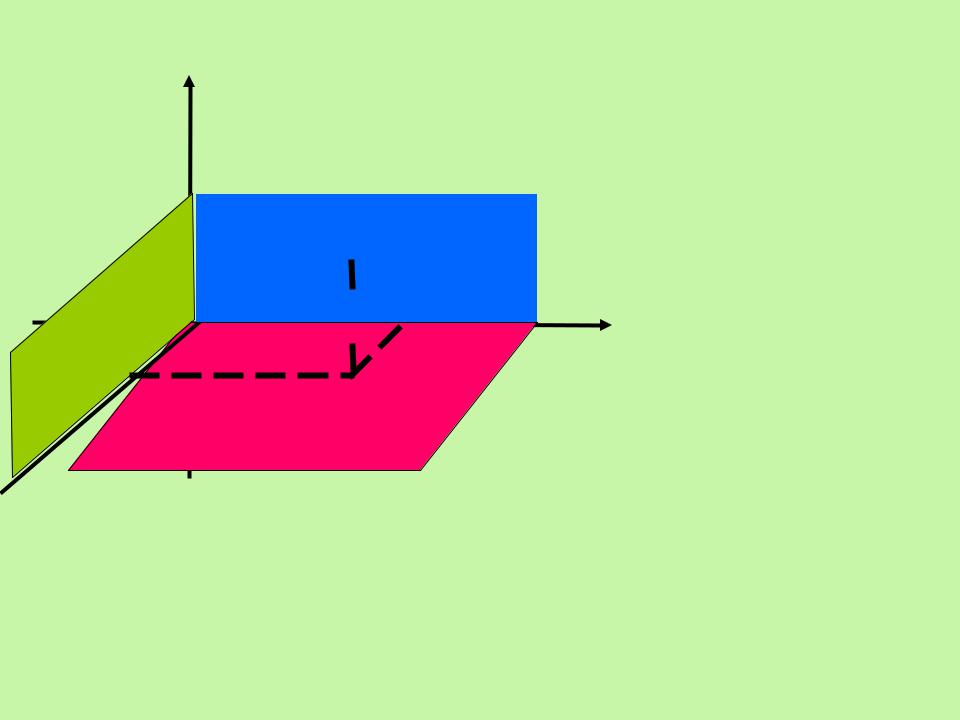
z
o у
Оy
Оz
Оy
Оz
Оx
Оx
X |
ОХ – ось абсцисс |
|
ОУ – ось ординат |
|
OZ – ось аппликат |
|
О – начало координат |
Нахождение координат точек.
Точка лежит
на оси |
|
в координатной плоскости |
|
|
|
Ох (х; 0; 0) |
|
|
Оху (х; у; 0) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оуz (0; у; z) |
|
|
|
|
|
|
|
Охz (х; 0; z) |
|
||||
|
Оу (0; у; 0) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ 400 – устно. |
|
|||
|
|
Оz (0; 0; z) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Прямоугольная система координат в
z |
пространстве |
|||
|
|
|
|
Оси: Ох, Оу, Оz |
|
|
|
|
Плоскости: Оху, Охz, Oyz |
|
|
|
М |
|
|
|
|
Охуz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у
М(х;у;z)
х
Ось Ох А(х;0;0) Ось Оу В(0;у;0) Ось Оz С(0;0;z)
Плоскость Оху L(х;у;0) Плоскость Охz N(x;0;z) Плоскость Оуz F(0;x;z)
Повторение:
Даны точки А ( - 1; 7 ) и В ( 7; 1).
а) Найдите координаты середины отрезка АВ.
хС |
|
хА хВ |
уС |
уА уВ |
||
|
|
|
||||
2 |
|
2 |
||||
|
|
|
|
|
||
|
|
|
С ( 3; 4) |
|
||
|
|
|
|
|
|
|
|
б) Найдите длину отрезка АВ. |
|||||
АВ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
хВ |
хА 2 уВ |
уА 2 |
||||
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|АВ| = 10 |
|
Даны точки А ( - 1; 7;3 ) и В ( 7; 1;-4).
а) Найдите координаты середины отрезка АВ.
хС |
хА хВ |
; |
уС |
уА уВ |
; |
zС |
zА zВ |
|
|
||||||||
|
||||||||
|
2 |
|
||||||
2 |
||||||||
|
|
|
|
2 |
||||
С ( 3; 4;...)
б) Найдите длину отрезка АВ.
|
АВ |
|
|
|
|
|
|
|
|
хВ хА 2 уВ |
уА 2 zB zA 2 |
||||
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|АВ| = ... |
|

№1 Точка М — середина отрезка АВ. Найдите координаты: а) точки М, если А(0;3;-4), В(-2;2;0); б) точки В, если А(14;-8;5), М(3;-2;-7); в) точки А, если В(0;0;2), М(-12;4;15)
№2 Дана точка М(-4;7;0) и N(0;-1;2). Найдите расстояние от начала координат до середины отрезка MN.
№3 Даны точки А(3\2;1;-2), В(2;2;-3) и С(2;0;-1). Найдите: а)периметр треугольника; б) медианы треугольника АВС.
№4* Определите вид треугольника АВС, если: а) А(9;3;-5), D(2;10;-5), C(2;3;2);
б) A(3;7;-4), B(5;-3;2), C(1;3;-10);
в) A(5;-5;-1), B(5;-3;-1), C(4;-3;0);
г) A(-5;2;0), B(-4;3;0), C(-5;2;-2)/
