
Лабораторные работы / Работа 1 - Долотов - 2007 / Статика 1
.docДля вычисления отделенного корня существует множество методов. Из них мы рассмотрим следующие: метод деления пополам, метод простой итерации, метод Ньютона и его модификации.
Простейшим методом является метод деления пополам, называемый также методом бисекций или методом дихотомии. Он состоит в следующем. Допустим, что удалось найти отрезок [a,b], на котором расположен один корень X. В качестве начального приближения к корню принимаем середину этого отрезка: x(0)=(a+b)/2. Далее исследуем значение функции f(x) на концах отрезков [a,x(0)] и [x(0),b], то есть в точках a, x(0), b. Тот из отрезков, на концах которого f(x) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового исследуемого отрезка. Вторую половину отрезка [a,b] не рассматриваем (так как корня там нет). В качестве первого приближения к корню принимаем середину нового отрезка и т.д. После каждого приближения (итерации) отрезок, на котором расположен корень, уменьшается вдвое, то есть после k-ой итераций он сокращается в 2k раз.
Математически формулы метода деления пополам представляются следующим образом:
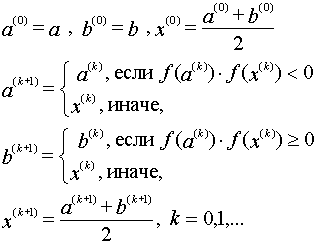
Итерационный процесс следует продолжать до тех пор, пока значение функции f после некоторой итерации с номером k+1 не станет по модулю меньше либо равно некоторого заданного малого числа , то есть | f(x (k+1)) | ≤ . После этого с погрешностью полагают: X x (k+1). Другим вариантом условия окончания итераций может служить (b (k+1) - a (k+1) )/ 2 ≤ . Это условие следует из очевидного неравенства:
|X - x (k+1)| ≤ (b (k+1) - a (k+1) )/ 2.
Схема гидравлической установки:
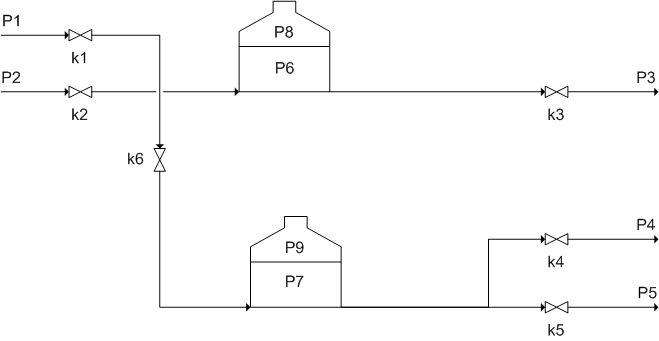
При расчете используются следующие уравнения:
1. V1 = k1 (P1 – P6)1/2
2. V2 = k2 (P2 – P6)1/2
3. V3 = k3 (P6 – P3)1/2
4. V4 = k4 (P7 – P4)1/2
5. V5 = k5 (P7 – P5)1/2
6. V6 = k6 (P6 – P7)1/2
7. P6=P8 + rgH1
8. P7=P9 + rgH2
9. P8 = PN( H1G/( H1G - H1 ))
10. P9 = PN( H2G/( H2G – H2 ))
11. V1 + V2 – V3 – V6 = 0
12. V6 - V5 – V4 =0
Информационная матрица имеет вид:
|
пп |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
P6 |
P7 |
P8 |
P9 |
H2 |
H1 |
№ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
11,12 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
11,12 |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
Блок-схема расчета:
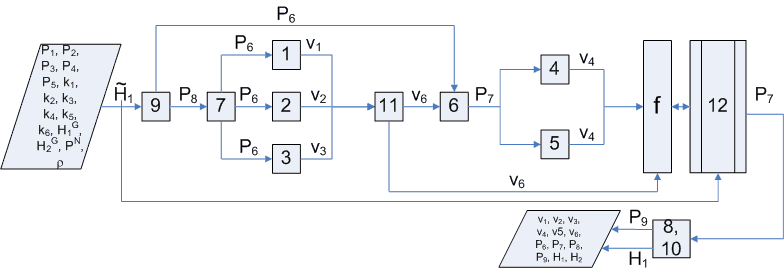
Листинг программы:
Public Sub stat()
ipr = 1
With Worksheets("Лист1")
hg(1) = .Cells(4, 5): hg(2) = .Cells(5, 5)
ro = .Cells(6, 5)
pn = .Cells(6, 9) / 0.000001
For i = 1 To 5: p(i) = .Cells(8, i + 4) / 0.000001: Next i
For i = 1 To 6: ak(i) = .Cells(9, i + 4) * .Cells(7, 9) / Sqr(ro): Next i
e = .Cells(11, 6)
kl = .Cells(10, 6)
End With
Worksheets("Лист2").Activate: Cells.Select: Selection.Clear: Range("a1").Select
Worksheets("Лист3").Activate: Range("a:b").Select: Selection.Clear: Range("a1").Select
If kl = 2 Then
Cells(ipr, 5) = "Промежуточный вывод": ipr = ipr + 1
Cells(ipr, 5) = "h": Cells(ipr, 6) = "p(6-9) /Па/": Cells(ipr, 7) = "vm": ipr = ipr + 1
End If
g = 9.815: e = e / 100: a = 0: b = hg(1) * (1 - e)
Call MPD(a, b, e, bu, x)
With Worksheets("Лист2")
If bu Then
a = ro * g
b = p(7) + ro * g * hg(2)
c = (p(7) - pn) * hg(2)
h(2) = (b - Sqr(b * b - 4 * a * c)) / 2 / a
p(9) = pn * hg(2) / (hg(2) - h(2))
.Cells(1, 1) = "РЕЗУЛЬТАТ"
.Cells(2, 1) = "h": .Cells(2, 2) = "p(6-9)": .Cells(2, 3) = "vm": .Cells(2, 4) = "v":
.Cells(3, 1) = h(1): .Cells(4, 1) = h(2):
For i = 6 To 9:
.Cells(i - 3, 2) = p(i) * 0.000001: Next i
For i = 1 To 6: vm(i) = v(i) * ro:
.Cells(i + 2, 3) = vm(i)
.Cells(i + 2, 4) = v(i): Next i
.Cells(i + 3, 3) = "общ.м.баланс :"
.Cells(i + 4, 3) = vm(1) + vm(2) + vm(3) - vm(4) - vm(5) - vm(6)
Else
kl = 2
.Cells(1, 1) = "РЕШЕНИЯ НЕТ"
.Cells(2, 1) = "a": .Cells(2, 2) = "f(a)": .Cells(2, 3) = "b": .Cells(2, 4) = "f(b)"
.Cells(3, 1) = a
.Cells(ipr, 5) = "Промежуточный вывод a": ipr = ipr + 1
.Cells(ipr, 5) = "h": .Cells(ipr, 6) = "p(7-10)": .Cells(ipr, 7) = "vm": ipr = ipr + 1
.Cells(3, 2) = FUNC(a)
.Cells(3, 3) = b
.Cells(1, 5) = "Промежуточный вывод b": ipr = ipr + 1
.Cells(2, 5) = "h": .Cells(2, 6) = "p(7-10)": .Cells(2, 7) = "vm": ipr = ipr + 1
Cells(3, 4) = FUNC(b)
End If
End With
With Worksheets("Лист3")
.Cells(2, 1) = "x": .Cells(2, 2) = "FUNC(x)"
For i = 1 To nv - 1
x = hg(1) * i / nv
.Cells(2 + i, 1) = x: .Cells(2 + i, 2) = FUNC(x)
Next i
End With
Worksheets("Лист2").Activate
End Sub
Function FUNC(x#) As Double
Dim fx#, i%
h(1) = x
p(8) = pn * hg(1) / (hg(1) - h(1))
p(6) = p(8) + ro * g * h(1)
v(1) = ak(1) * Sgn(p(1) - p(6)) * Sqr(Abs(p(1) - p(6)))
v(2) = ak(2) * Sgn(p(2) - p(6)) * Sqr(Abs(p(2) - p(6)))
v(3) = ak(3) * Sgn(p(6) - p(3)) * Sqr(Abs(p(6) - p(3)))
v(6) = v(1) + v(2) - v(3)
p(7) = p(6) - Sgn(v(6)) * (v(6) / ak(6)) ^ 2
v(4) = ak(4) * Sgn(p(7) - p(4)) * Sqr(Abs(p(7) - p(4)))
v(5) = ak(5) * Sgn(p(7) - p(5)) * Sqr(Abs(p(7) - p(5)))
fx = (v(4) + v(5) - v(6)) * ro
For i = 1 To nk: vm(i) = v(i) * ro: Next i
If kl = 0 Then GoTo 400
If kl = 1 Then GoTo 300
Cells(ipr, 5) = h(1): Cells(ipr, 6) = p(7): Cells(ipr, 7) = vm(1): ipr = ipr + 1
Cells(ipr, 6) = p(9): Cells(ipr, 7) = vm(2): ipr = ipr + 1
Cells(ipr, 6) = p(8): Cells(ipr, 7) = vm(3): ipr = ipr + 1
Cells(ipr, 7) = vm(4): ipr = ipr + 1
Cells(ipr, 7) = vm(5): ipr = ipr + 1
Cells(ipr, 7) = vm(6): ipr = ipr + 1
Cells(ipr, 7) = vm(7): ipr = ipr + 1
Cells(ipr, 7) = p(10)
300: Cells(ipr, 5) = "x = ": Cells(ipr, 6) = x: Cells(ipr, 7) = " fx = ": Cells(ipr, 8) = fx: ipr = ipr + 1
400: FUNC = fx
End Function
Sub MPD(a#, b#, eps#, bu As Boolean, xcon#)
Dim fa#, fb#, x#, fx#
fa = FUNC(a): fb = FUNC(b)
If fa * fb > 0 Then: bu = False: GoTo 100
Do
x = (a + b) / 2: fx = FUNC(x)
If fx * fa < 0 Then b = x Else a = x
Loop While Abs(a - b) > eps
xcon = Abs(a + b) / 2: bu = True
100:
End Sub
Sub auto_open()
Worksheets("Лист1").Activate
End Sub
Российский Химико-Технологический Университет
им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
Лабораторная работа № 1
Построение и расчёт модели статической
гидравлической системы
Выполнил студент гр. О-44
Майков А.
Москва
2007
Российский Химико-Технологический Университет
им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
Лабораторная работа № 1
Построение и расчёт модели статической
гидравлической системы
Выполнил студент гр. О-44
Долотов О.
Москва
2007
Российский Химико-Технологический Университет
им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
Лабораторная работа № 1
Построение и расчёт модели статической
гидравлической системы
Выполнила студентка гр. О-44
Стрелкова А.
Москва
2007
