TMM кр

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНЖЕНЕРНЫХ ТЕХНОЛОГИЙ»

КАФЕДРА ТЕХНИЧЕСКОЙ МЕХАНИКИ

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Теория механизмов и машин»

Тема: «Структурный анализ плоских и пространственных кинематических цепей. Классификация механизмов».

Выполнил студент: 2 курса дистанционного обучения

Направление: 150302с

“Технологические машины и оборудование”

Шифр: 14-012

Ф.И.О.

Проверил: Е.В.Матвеева

Вариант 13.

Задание 1.

Дана структурная схема пространственного робота-

манипулятора.

Необходимо:

- определить число подвижных звеньев кинематической цепи;

- определить цепь замкнутая или разомкнутая, простая или

сложная;

- выписать все кинематические пары и дать их название;

- установить класс и степень подвижности каждой кинемати-

ческой пары;

- определить степень подвижности, заданной кинематической

цепи;

Решение:

Кинематическую цепь образуют пять подвижных звеньев

(n=4). Нумерация их показана на приведенном ниже рисунке.

Классификацию всех кинематических пар представим в табл. 2.

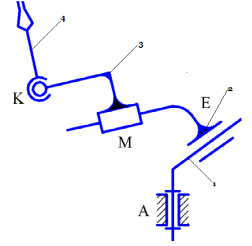
Табл2

Звенья образующие пару	0-1	1-2	2-3	3-4
Обозначение	А	Е	М	К
Название	Вращательная	Цилиндрическая	Поступательная	Сферическая
Класс пары	5	4	5	3
Подвижность	1	2	1	3

Исследуемая кинематическая цепь является простой, так как каждое подвижное звено входит не более чем в две кинематические пары, и разомкнутой, так как звено 4 входит только в одну кинематическую пару.

Так как рассматриваемая кинематическая цепь пространственная, степень ее подвижности рассчитаем по формуле Сомова-Малышева:

W=6n-5p5-4p4-3p3-2p2-1p1 ,

где p5, p4, p3, p2 и p1 –число кинематических пар соответствующего класса. В результате получим:

W=6·5-5·2-4·1-3·1-2·0-1·0=7.

Задание 2

Дана структурная схема плоского механизма.

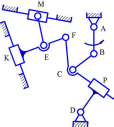
Рисунок 1 Структурная схема плоского механизма

Необходимо:

• определить число подвижных звеньев кинематической цепи;

• определить цепь замкнутая или разомкнутая, простая или сложная;

• выписать все кинематические пары и дать их название;

• установить класс и степень подвижности каждой кинематической пары;

• определить степень подвижности заданной кинематической цепи;

• разбить механизм на структурные группы Ассура;

• выписать кинематические пары, которыми группа Ассура соединяется с основным механизмом и определить порядок каждой структурной группы;

• для каждой структурной группы третьего и выше класса выписать ки-нематические пары, образующие наиболее сложный внутренний замкнутый контур и определить класс каждой структурной группы;

• определить класс механизма;

• записать схему образования механизма.

Решение:

Кинематическую цепь образуют девять подвижных звеньев (n = 7). Нумерация показана на рисунке. Классификацию всех кинематических пар

приведем в таблице 1.
0			0
7			1
6			2
5			3
0			4
			0
Рисунок 2 - Нумерация подвижных звеньев
Таблица 1 Классификация кинематических пар
Звенья, образующие пару	Обозначение		Название
0-1	Вращательная		А
1-2	Вращательная		В
2-3	Вращательная		С
0-4	Вращательная		D
5-6	Вращательная		E
3-5	Вращательная		F
0-5	Поступательная		K
6-7	Вращательная		M/
0-7	Поступательная		M//
3-4	Поступательная		P

Исследуемая кинематическая цепь является сложной, так как в ней имеются подвижные звенья, входящие более чем в две кинематические пары (звенья 3 и 5) и замкнутой, так как каждое подвижное звено входит в две и более кинематические пары.

Все кинематические пары относятся к кинематическим парам пятого класса. Их общее число - 10 (р₅= 10). Рассчитаем степень подвижности цепи по формуле Чебышева:

W = 3n - 2p₅ - 1p₄ = 3·7 - 2·10 - 1·0 = 1.

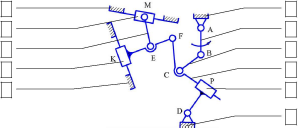
Выделим из рассматриваемой цепи структурные группы Ассура, т.е. кинематические цепи с нулевой степенью подвижности, следя за тем, чтобы оставшаяся цепь была замкнутой. Первой отсоединяем группу из двух под-вижных звеньев (6, 7) и трех кинематических пар: (5-6; 6-7; 7-0). Это группа Ассура второго(II)класса.

Отсоединенная группа двумя кинематическими парами (5-6) и (7-0) соединяется с основным механизмом, следовательно, порядок этой группы –

второй.

Отсоединенная группа и остаток показаны на рисунке.

0			0
7
			1
6
			2
	5		3
	0		4
			0
	Рисунок 2 - Отсоединенная группа и остаток

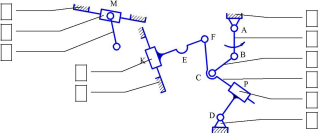
Выделим из оставшейся кинематической цепи следующую структур-ную группу. Это цепь из четырех подвижных звеньев (2, 3, 4 и 5) и шести ки-нематических пар – (0-5; 3-5; 0-4; 3-4; 2-3; 1-2). Изобразим остаток.

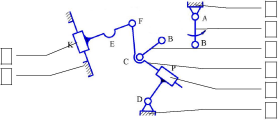
	0
	1
5	2
	3
0
	4
	0
	Рисунок 3 - Отсоединенная группа и остаток

Отсоединенная группа тремя кинематическими парами (0-5; 0-4 и 1-2) соединяется с основным механизмом, следовательно,порядок этой группы

– третий.

Внутренний замкнутый контур в отсоединенной цепи один он образо-ван кинематическими парами (3-5; 4-5; 2-3). Их три, следовательно, это группа Ассура третьего класса(III).

В остатоке осталось входное звено, присоединенное к стойке, т.е.про-

стейший механизм первого класса.

Таким образом, механизм включает в себя одну группу Ассура второго класса и одну группу Ассура третьего класса.Наивысший класс структур-ной группы –третий, следовательно, это механизм третьего класса. Запи-шем схему образования механизма:

I(1) + III(2;3;4;5) +II(6;7) = M(III).

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Артоболевский, И. И.Теория механизмов и машин[Текст] :учебник

• И. И. Артоболевский. -М. : ИД Альянс, 2011.- 640 с.

2. Чернухин, Ю. В.Теоретическая механика.Теория меха-низмов и ма-шин [Текст] : учеб. пособие / Ю. В. Чернухин, А. В. Колтаков, А. В. Некра-сов; Воронеж. гос. ун-т инж. технол. – Воронеж : ВГУИТ, 2011. – 120 с.

Воронеж 2015