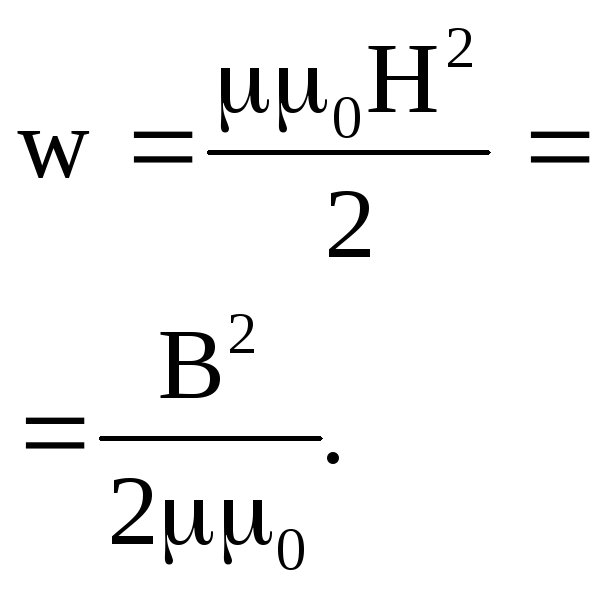2-2. Основные формулы

Сила взаимодействия точечных зарядов (закон Кулона)

где F - сила взаимодействия двух точечных зарядов и , направленная вдоль прямой, соединяющей их центры; r - расстояние между зарядами; - диэлектрическая проницаемость среды; - электрическая постоянная.

,

Вектор напряженности электрического поля

.

Напряженность электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда

.

Напряженность электрического поля, создаваемого металлической сферой радиусом R с общим зарядом q, на расстоянии r от центра сферы

а) внутри сферы (r<R)

Е=0;

б) на поверхности сферы (r=R)

;

в) вне сферы (r>R)

.

Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) на расстоянии r от ее (его) оси

где - линейная плотность заряда.

,

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью

где - поверхностная плотность заряда.

,

Напряженность поля в пространстве между двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями с одинаковой по величине поверхностной плотностью заряда

.

Потенциал электрического поля

где - потенциальная энергия точечного заряда q₀, помещенного в данную точку поля.

,

Потенциал электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда

.

Потенциал электрического поля, создаваемого металлической сферой радиусом R с общим зарядом q, на расстоянии r от центра сферы

а) внутри сферы (r<R)

;

б) на поверхности сферы (r=R)

;

в) вне сферы (r>R)

.

Связь потенциала с напряженностью электрического поля

.

Вектор электрического смещения

.

Поток вектора через произвольную поверхность S

где Е_n – проекция вектора на направление нормали к элементарной площадке dS.

,

Если поле однородно, поверхность S - плоская, то

где - угол между вектором и нормалью к поверхности S.

,

Теорема Остроградского-Гаусса

где - поток вектора напряженности через произвольную замкнутую поверхность S, охватывающую заряды q₁, q₂, …q_n.

,

Энергия W_П взаимодействия системы точечных зарядов , , …,

где - потенциал поля, создаваемого всеми зарядами (за исключением i-го) в точке, где расположен заряд .

,

Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал , в другую, имеющую потенциал

А=q(-)= =.

Электрическая емкость уединенного проводника

где q- заряд проводника, - его потенциал.

,

Электрическая емкость конденсатора

где q- заряд конденсатора, - разность потенциалов между обкладками конденсатора.

,

Электрическая емкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью

.

Электрическая емкость плоского конденсатора

где S - площадь каждой из обкладок конденсатора; d - расстояние между обкладками; - диэлектрическая проницаемость диэлектрика, заполняющего пространство между обкладками.

,

Электрическая емкость плоского слоистого конденсатора

где d_i – толщина i-того слоя диэлектрика, -его диэлектрическая проницаемость.

,

Электрическая емкость сферического конденсатора (две концентрические сферы радиусами и , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью )

.

Электрическая емкость цилиндрического конденсатора (два коаксиальных цилиндра длиной L и радиусами и , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью )

.

Электроемкость батареи конденсаторов, соединенных

последовательно

;

параллельно

где С_i – емкость i-того конденсатора, N – число конденсаторов.

,

Энергия электрического поля заряженного проводника

где q - заряд, - потенциал, С - электрическая емкость проводника.

Энергия электрического поля заряженного конденсатора

где С - электрическая емкость конденсатора; U - разность потенциалов на его обкладках.

Объемная плотность энергии электрического поля

где Е - напряженность электрического поля в среде с диэлектрической проницаемостью ; D - электрическое смещение.

Сила тока

.

Плотность тока

.

Сопротивление однородного проводника

где - удельное сопротивление, - длина, S - площадь поперечного сечения проводника.

,

Сопротивление при последовательном и параллельном соединении проводников

где R_i – сопротивление i – того проводника, N – число проводников.

,,

Закон Ома в дифференциальной форме

где - удельная электрическая проводимость, - напряженность электрического поля.

,

Закон Ома для однородного участка цепи

где I - сила тока, текущего по однородному проводнику, U - напряжение на его концах, R - электрическое сопротивление проводника.

,

Закон Ома для неоднородного участка цепи в интегральной форме

где - суммарная ЭДС на данном участке, R - суммарное сопротивление внешней цепи, r - внутреннее сопротивление источника ЭДС.

Закон Ома для замкнутой цепи

.

Закон Джоуля-Ленца в дифференциальной форме

где w – тепловая мощность тока, - удельная электрическая проводимость, - напряженность электрического поля.

,

Закон Джоуля - Ленца в интегральной форме

где dQ- количество теплоты, выделяющейся в неподвижном и химически не изменяющемся проводнике при протекании через него тока силой I в течение времени dt.

Мощность в цепи постоянного тока

полная (выделяющаяся во всей замкнутой цепи)

,

полезная (выделяющаяся на внешнем сопротивлении R)

К.П.Д. источника тока

Правила Кирхгофа

Первое. Алгебраическая сумма сил токов, сходящихся в узле, равна нулю

Второе. В любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС , встречающихся в этом контуре.

Сила Ампера

в векторной форме:

,

в скалярной форме:

где - элемент тока, - индукция магнитного поля, - угол между векторами и .

,

Магнитный момент замкнутого контура площадью S с током I

где - единичный вектор положительной нормали к плоскости контура, направление которого связано с направлением тока правилом правого винта.

,

Механический момент сил, действующих на контур с током, помещенный в магнитное поле с индукцией

в векторной форме:

,

в скалярной форме:

где - угол между векторами и .

Сила Лоренца

в векторной форме:

,

в скалярной форме:

где q – заряд частицы, - ее скорость, - индукция магнитного поля, - угол между векторами и .

Закон Био-Савара-Лапласа

в векторной форме:

где - магнитная индукция поля, создаваемого элементом тока I; -радиус-вектор точки, в которой определяется магнитная индукция; - магнитная проницаемость окружающей проводник среды, - магнитная постоянная.

,

в скалярной форме:

где - угол между векторами I и .

Индукция магнитного поля в центре кругового проводника (витка) с током I

где r - радиус витка.

,

Индукция магнитного поля, создаваемого бесконечно длинным прямым проводником с током I в точке, находящейся на расстоянии r от оси проводника

.

Индукция магнитного поля, создаваемого отрезком проводника с током

.

Индукция магнитного поля, создаваемого соленоидом с током I в средней его части (или тороидом на его оси)

где n - число витков, приходящихся на единицу длины соленоида.

,

Связь индукции с напряженностью магнитного поля (в случае однородной, изотропной среды)

.

Элементарный поток вектора индукции магнитного поля (магнитный поток) через площадку dS

где -угол между направлением вектора и нормалью к площадке , В_n - проекция вектора на направление нормали к площадке.

Поток вектора индукции магнитного поля через произвольную поверхность S

Потокосцепление (полный поток сквозь N витков):

.

Элементарная работа по перемещению контура с током I в магнитном поле

где dФ - изменение магнитного потока, пронизывающего поверхность, ограниченную контуром.

,

Работа при произвольном перемещении контура в магнитном поле

.

Магнитный поток, сцепленный с соленоидом (катушкой содержащей N витков)

где L – индуктивность контура (коэффициент самоиндукции).

,

Закон электромагнитной индукции (закон Фарадея - Максвелла)

где электродвижущая сила индукции, N - число витков контура.

,

Электродвижущая сила самоиндукции

.

Индуктивность соленоида

где - число витков на единицу длины соленоида, S – площадь сечения соленоида, - его длина, - объем соленоида, - магнитная постоянная, - магнитная проницаемость среды.

,

,

Энергия магнитного поля соленоида (катушки) с индуктивностью L при силе тока I

.

Объемная плотность энергии магнитного поля

Скорость распространения электромагнитных волн (света) в среде

где с – скорость света в вакууме, - диэлектрическая проницаемость среды, - магнитная проницаемость среды, n – абсолютный показатель преломления среды.

,

Длина волны света в среде

где - длина волны в вакууме, n - абсолютный показатель преломления среды.

,

Оптическая разность хода двух световых волн

где и - оптические длины путей световых волн в различных средах, и - абсолютные показатели преломления сред, и - геометрические длины путей световых волн соответственно в средах с показателями преломления и .

Связь разности фаз двух волн () с их оптической разностью хода ()

.

Оптическая разность хода волн (), отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе:

а) в отраженном свете:

или

;

б) в проходящем свете:

где d - толщина пластинки (пленки), - угол падения света на пластинку, - угол преломления, n - относительный показатель преломления материала пластинки (пленки).

или

,

Условие максимума интенсивности при интерференции двух когерентных волн

где - оптическая разность хода.

,

k= 0, 1, 2, 3...

Условие минимума интенсивности при интерференции двух когерентных волн

, k= 0, 1, 2, 3...

Положение максимумов и минимумов интенсивности света при интерференции волн от двух когерентных источников (метод Юнга)

где d - расстояние между двумя когерентными источниками (отверстиями в методе Юнга), находящимися на расстоянии L от экрана, параллельного обоим источникам, при условии L >> d.

,

k= 0, 1, 2, 3...,

k= 0, 1, 2, 3...,

Ширина интерференционной полосы при интерференции волн от двух когерентных источников

.

Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем)

где k - номер кольца, R - радиус кривизны линзы.

k = 1, 2, 3 ...

Радиусы темных колец Ньютона в отраженном свете (или светлых в проходящем)

,

k = 1, 2, 3 ...

Радиусы зон Френеля

для сферической волны

,

для плоской волны

где a - расстояние от диафрагмы с отверстием (щелью) до точечного источника света, b - расстояние от диафрагмы до точки наблюдения (экрана), k - номер зоны Френеля.

,

При дифракции Френеля на круглом отверстии в центре экрана будет наблюдаться

а) максимум интенсивности (светлое пятно), если в отверстие укладывается нечетное число зон Френеля;

б) минимум интенсивности (темное пятно), если в отверстие укладывается четное число зон Френеля.

Дифракция Фраунгофера на одной щели при нормальном падении лучей

Условие минимума интенсивности света

,

k = 1, 2, 3, . . .

Условие максимума интенсивности света

где а - ширина щели, - угол дифракции, k —номер максимума (минимума).

,k = 1, 2, 3, . . .

Положение главных максимумов при дифракции света на дифракционной решетке при нормальном падении лучей

где d - период (постоянная) решетки, k - номер главного максимума (порядок спектра), - угол дифракции.

,

k = 0, 1, 2, . . .,

Разрешающая способность дифракционной решетки

где - наименьшая разность длин волн двух соседних спектральных линий, видимых раздельно, N - общее число штрихов решетки, k - порядок спектра.

R = = kN,

Угловая дисперсия дифракционной решетки

где - угловое расстояние между двумя спектральными линиями, отличающимися по длине волны на .

,

Формула Вульфа – Брэггов

где d –расстояние между атомными плоскостями кристалла, -угол скольжения рентгеновских лучей, k – номер дифракционного максимума.

,

k = 1, 2, 3, . .

Закон Брюстера

где - угол падения, при котором отраженный луч полностью поляризован, - относительный показатель преломления.

,

Закон Малюса

где I - интенсивность света, прошедшего через анализатор, I₀ - интенсивность плоскополяризованного света, падающего на анализатор, - угол между плоскостью поляризации волны, падающей на анализатор, и плоскостью пропускания анализатора.

,

Степень поляризации света

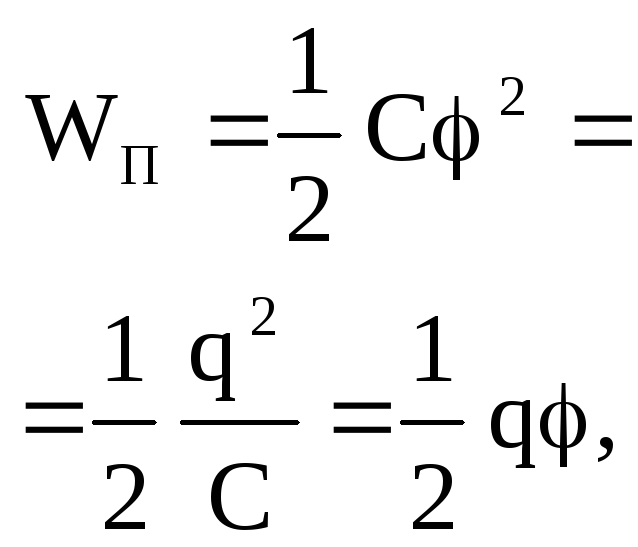
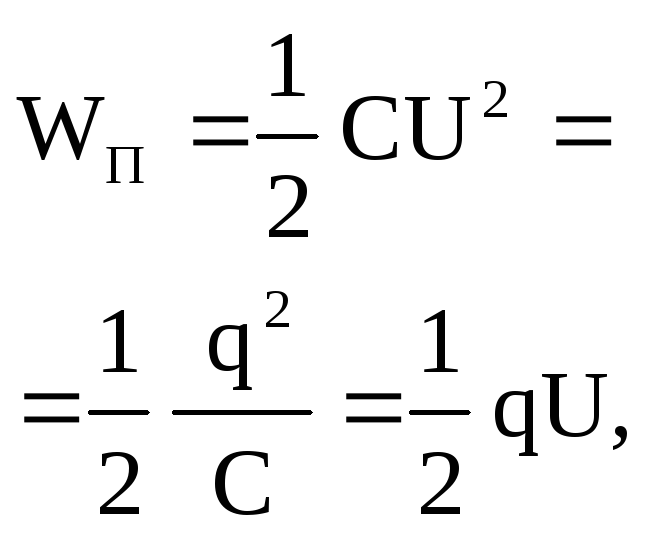
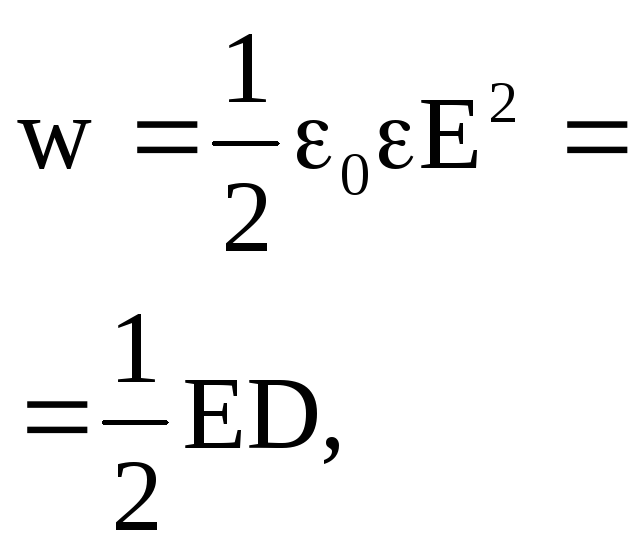
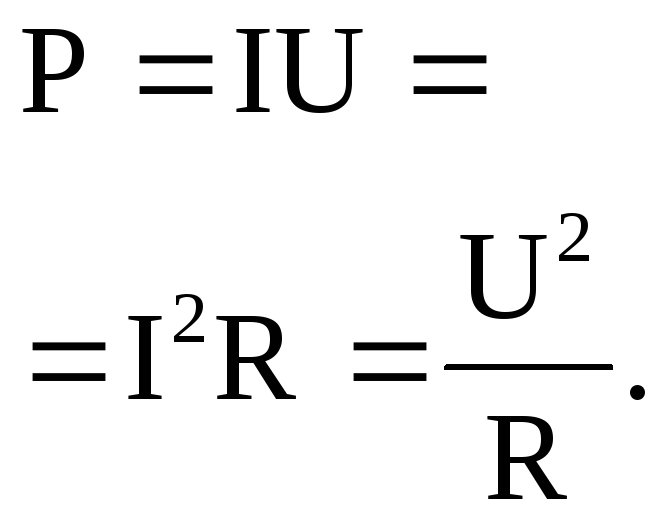
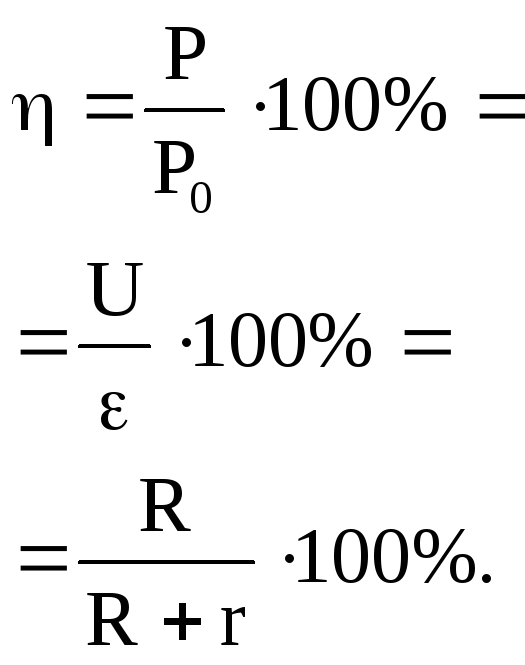
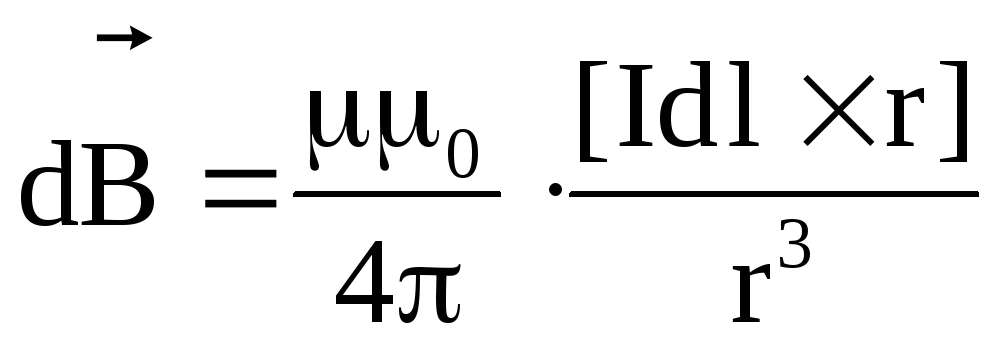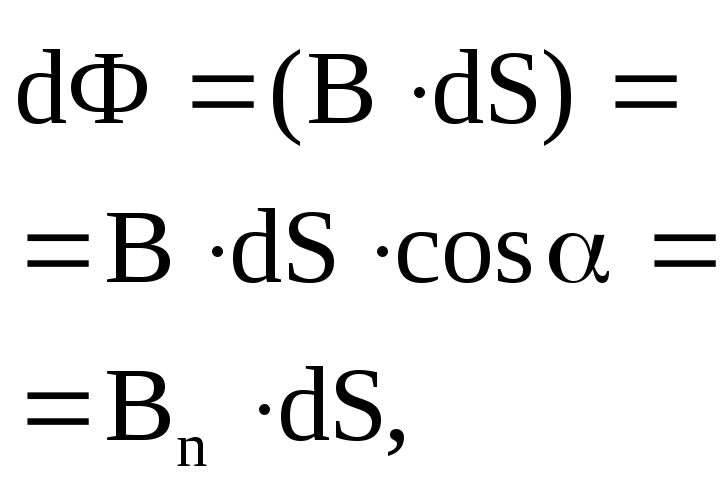
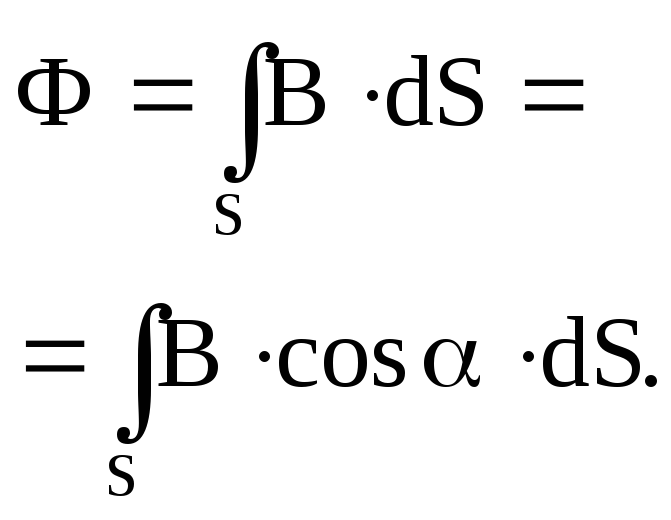
где и - максимальная и минимальная интенсивности частично - поляризованного света, пропускаемого анализатором.

,