
Методика изучения интеграла
.docТема: Методика изучения интеграла
План:
-
Понятие первообразной
-
Криволинейная трапеция
-
Применение интегралов для вычисления площадей и объемов фигур
(1) Перед введением понятия интеграла
вводится понятие первообразной. Поэтому
необходимо повторять понятие производной,
физического смысла производной. С этой
целью целесообразно провести математический
диктант с последующей проверкой. Вопросы
типа:
![]()
Хотим показать, что для любой функции производная единственна, а для первообразной
производной может быть несколько функций.
Обратим внимание учащихся на то, что разные функции могут иметь одну и туже производную. И с точки зрения физики важно знать путь, зная скорость.
Проблема, как найти закон движения, если известен закон скорости. Учащиеся знают, что по закону движения можно найти закон скорости с помощью операции дифференцирования. Возникает обратная проблема. Эти операции в математике получили новое название – интегрирование.
Прежде чем вводить понятие интегрирование, как правило, сначала рассматривается понятие первообразной. В слабом классе путем практической работы для конкретных функций. Как закон скорости восстановить закон движения.

Приводим 5-6 примеров и убеждаем учащихся в том, что можно восстановить функцию по ее производной.
Функция
![]() называется первообразной функции
называется первообразной функции
![]() на заданном промежутке, если для
на заданном промежутке, если для
![]() из этого промежутка
из этого промежутка
![]() .
.
Для того, чтобы учащиеся сознательно
отличали производную от первообразной
на первых парах должен быть четкий
алгоритм
![]() .
.
После закрепления понятия первообразной изучаются ее свойства:
-
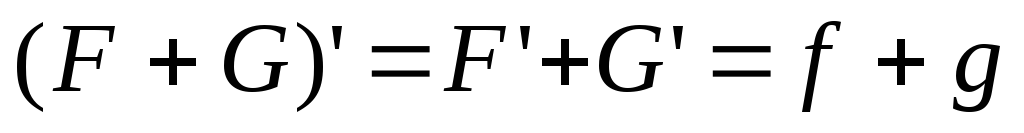 - первообразная суммы равна сумме
первообразных.
- первообразная суммы равна сумме
первообразных. -
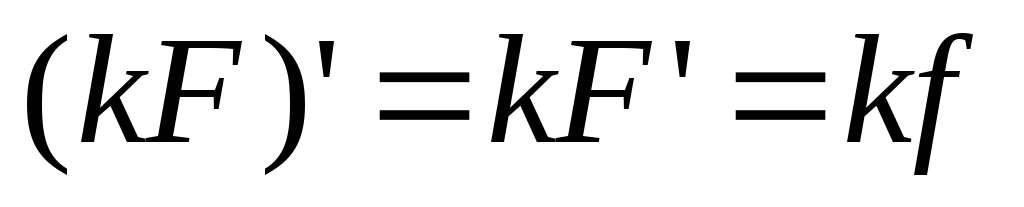 - постоянный множитель можно вынести
за знак первообразной.
- постоянный множитель можно вынести
за знак первообразной. -
По правилу вычитания производной сложной функции имеем:
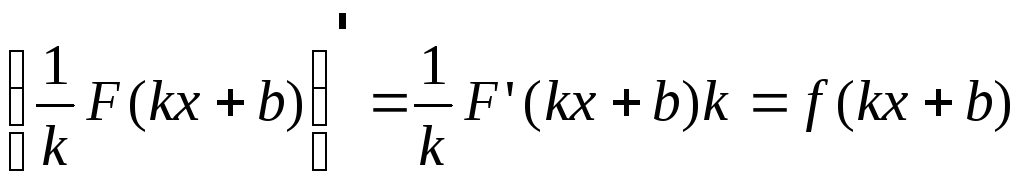 .
.
Эти свойства должны быть проиллюстрированы на конкретных примерах и теоретически обоснованы.
Изучение этих свойств может быть проведено в проблемно-поисковом плане. Пример: для подготовки доказательства признака постоянства функций предложить учащимся (1-2 человека) подготовить это доказательство.
План доказательства:
-
Один ученик у доски записывает это доказательство.
-
Второй ученик работает с классом фронтально. Разбивает доказательство по шагам. Все остальные записывают это доказательство в тетрадь. На конкретных примерах доказывают, что
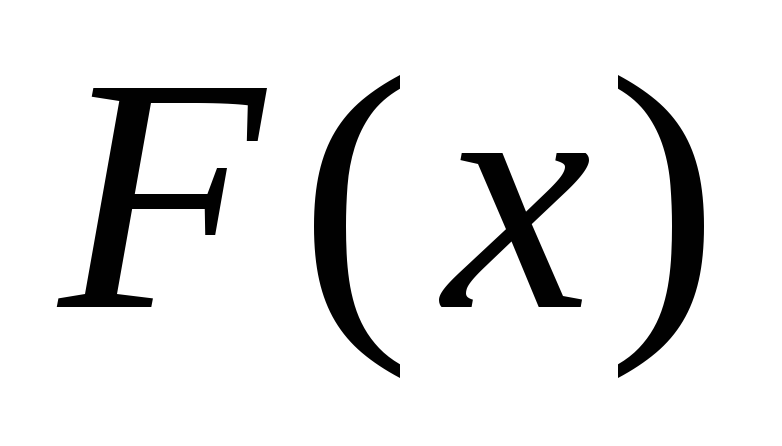 является первообразной для
является первообразной для
 на промежутке. Например:
на промежутке. Например:
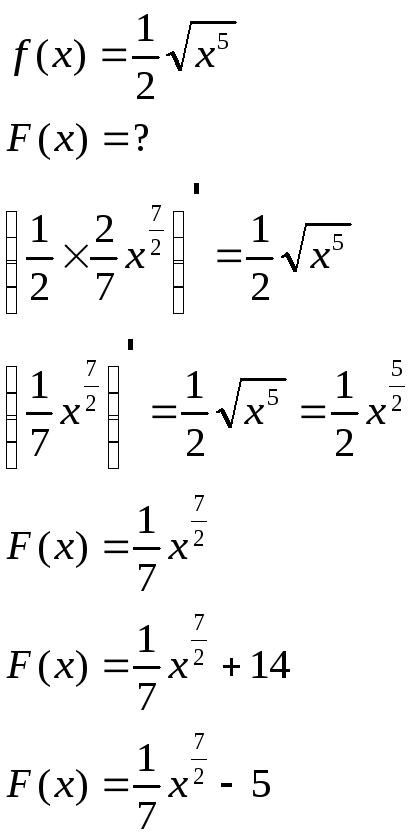
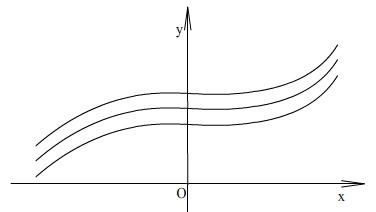
Семейство первообразных.
Любая первообразная для этой функции
будет иметь вид:
![]() .
.
Теорема. Любая первообразная для функции
![]() на промежутке может быть записана в
виде
на промежутке может быть записана в
виде
![]() .
.
Продемонстрировать закрепление этой теоремы упражнениями типа:
-
Доказать, что функция является первообразной функции…
-
Найти первообразную функции
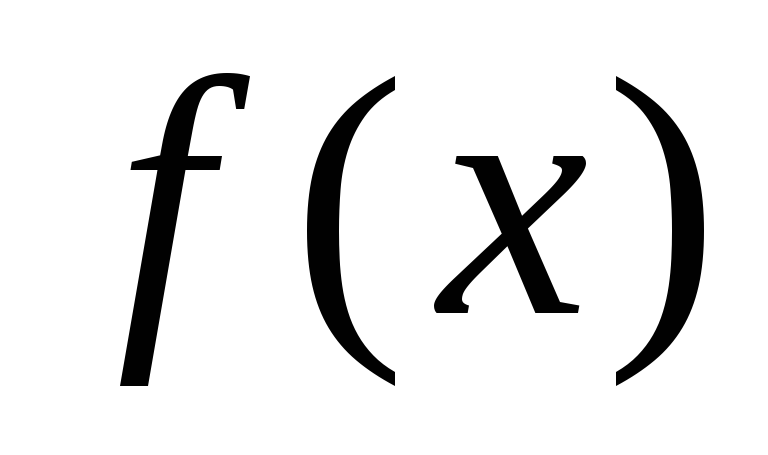
Проблемный вопрос: как зафиксировать некоторую первообразную из семейства первообразных? Оказывается, достаточно найти первообразную и подставить вместо аргумента ее значение.
Другой тип упражнения:

![]()
![]()
![]()
При доказательстве теоремы после
предварительной работы идет рассмотрение
конкретных примеров и обобщение в
результате ответа на вопрос: как доказать,
что
![]() - тоже первообразная для
- тоже первообразная для
![]() ?
?
Если известно, что
![]() является первообразной для
является первообразной для
![]() ,
то по определению первообразной находим
производную от
,
то по определению первообразной находим
производную от
![]() .
Она будет равна
.
Она будет равна
![]() .
.
![]()
Фактически доказали теорему по
определению. После доказательства
рассмотрим конкретную функцию
![]() .
Задание:
.
Задание:
-
Запишите любые первообразные для функции
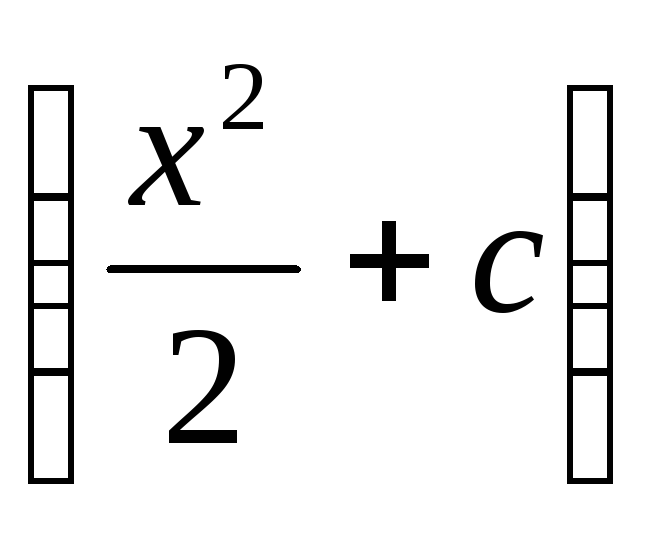
-
Запишите три первообразных для функции
-
Что является геометрическим образом первообразной?
-
Как получить из графика
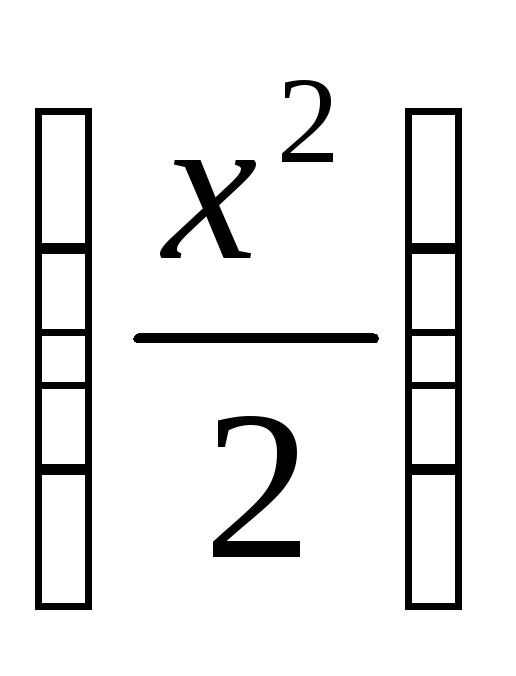 любой другой график?
любой другой график?
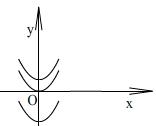
Предложить учащимся не график функции, а график первообразной и дать задание найти саму функцию.
![]()
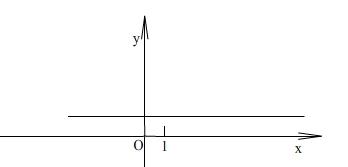
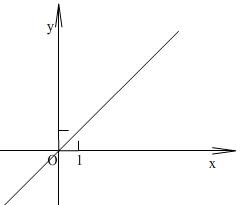
По графику первообразной спрашиваем у учащихся, график какой функции в каждой точке имеет угловой коэффициент равный единице? Построить график этой функции.
После рассмотрения этих вопросов составляется таблица первообразных.
![]() - по таблице производных это
- по таблице производных это
![]() .
А если соображать по определению
.
А если соображать по определению
![]() .
.
(2) Криволинейная трапеция.
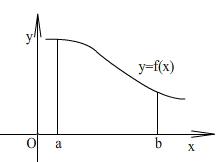
Фигуру, ограниченную графиком функции
![]() ,
параллельными прямыми
,
параллельными прямыми
![]() ,
отрезком
,
отрезком
![]() ,
называют криволинейной трапецией.
,
называют криволинейной трапецией.
Абстрактно дедуктивный метод: без
подготовки вводим любое определение.
После введения определения криволинейной
трапеции и отработки (закрепления этого
понятия) с применением конкретных
примеров необходимо сформулировать
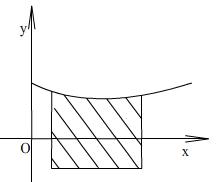
представление учащихся о том, что площадь
криволинейной трапеции будет функция,
если
![]() брать из отрезка
брать из отрезка
![]() .
.


То есть, каждому значению
![]() из промежутка
из промежутка
![]() будет соответствовать свое значение
площади.
будет соответствовать свое значение
площади.
![]() - площадь криволинейной трапеции
- площадь криволинейной трапеции
![]()
Подошли к теореме интеграла Ньютона-Лейбница.
![]()
После введения понятия криволинейной трапеции можно ввести определение интеграла.
![]()
(3) Применение интегралов для вычисления площадей и объемов фигур.

![]()
Работа:
![]()
Работа электрического поля по перемещению
одного заряда из
![]() в
в
![]() :
:
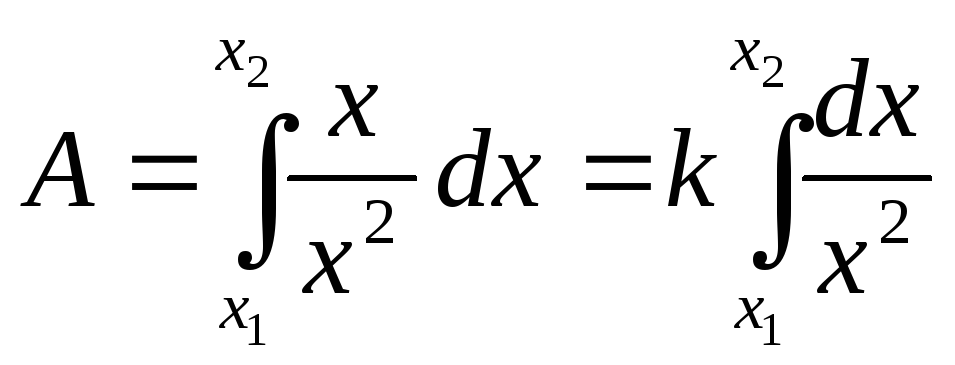
Масса:
![]()
Электрический ток:
![]()
Дополнение.
Мишин
Теорема. Пусть
![]() - непрерывная функция, неотрицательная
на отрезке
- непрерывная функция, неотрицательная
на отрезке
![]() ,
,
![]() - площадь соответствующей криволинейной
трапеции. Если
- площадь соответствующей криволинейной
трапеции. Если
![]() есть первообразная для
есть первообразная для
![]() на отрезке
на отрезке
![]() ,
то
,
то
![]() (рис. 1).
(рис. 1).
Рассмотрим функцию
![]() ,
определенную на отрезке
,
определенную на отрезке
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
Если
.
Если
![]() ,
то
,
то
![]() - площадь части криволинейной трапеции,
расположенной левее прямой, проходящей
через точку
- площадь части криволинейной трапеции,
расположенной левее прямой, проходящей
через точку
![]() .
При этом
.
При этом
![]() .
Докажем, что
.
Докажем, что
![]() .
Приведем одно из доказательств этого
утверждения, по аналогии с которым будет
позже доказано утверждение
.
Приведем одно из доказательств этого
утверждения, по аналогии с которым будет
позже доказано утверждение
![]() ,
где
,
где
![]() - площадь сечения для объема тела.
- площадь сечения для объема тела.
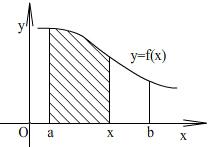
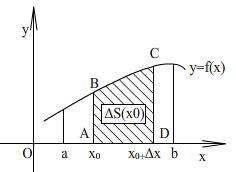
Рис 1, 2.

Рис 3.
Пусть функция
![]() непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке
![]() .
Каждому значению
.
Каждому значению
![]() из этого отрезка соответствует площадь
из этого отрезка соответствует площадь
![]() криволинейной трапеции; при этом
криволинейной трапеции; при этом
![]() -
площадь криволинейной трапеции,
соответствующей отрезку
-
площадь криволинейной трапеции,
соответствующей отрезку
![]() .
Докажем сначала, что
.
Докажем сначала, что
![]() для всех
для всех
![]() на
интервале
на
интервале
![]() .
Пусть
.
Пусть
![]() .
Рассмотрим значение
.
Рассмотрим значение
![]() из этого интервала. Приращение функции
выразится разностью
из этого интервала. Приращение функции
выразится разностью
![]() ,
которая равна площади криволинейной
трапеции
,
которая равна площади криволинейной
трапеции
![]() с основанием, равным
с основанием, равным
![]() ,
если
,
если
![]() ,
и площади этой криволинейной трапеции,
взятой со знаком «минус», если
,
и площади этой криволинейной трапеции,
взятой со знаком «минус», если
![]() .
.
Таким образом, можно записать, что
площадь криволинейной трапеции
![]() выразится как
выразится как
![]() (рис. 2, 3).
(рис. 2, 3).
Так как функция
![]() непрерывна в точке
непрерывна в точке
![]() ,
то выполняется условие
,
то выполняется условие
![]() .
Это означает, что для любого положительного
.
Это означает, что для любого положительного
![]() найдется
такое положительное число
найдется
такое положительное число
![]() ,
что для всех
,
что для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() ,
или
,
или
![]() (1).
(1).

Рис. 4.
Если
![]() ,
то для всех
,
то для всех
![]() ,
таких, что
,
таких, что
![]() при
при
![]() (или
(или
![]() при
при
![]() ),
неравенство (1) выполняется. Поэтому
(рис. 4) криволинейная трапеция с
основанием, равным
),
неравенство (1) выполняется. Поэтому
(рис. 4) криволинейная трапеция с
основанием, равным
![]() ,
содержит в себе прямоугольник с тем же
основанием и высотой
,
содержит в себе прямоугольник с тем же
основанием и высотой
![]() и в то же время содержится внутри
прямоугольника с тем же основанием и
высотой
и в то же время содержится внутри
прямоугольника с тем же основанием и
высотой
![]() .
Значит,
.
Значит,
![]() .
Поэтому для всех
.
Поэтому для всех
![]() выполняется условие
выполняется условие
![]() (2).
(2).
Так как
![]() - возрастающая функция (площадь
криволинейной трапеции увеличивается
с увеличением
- возрастающая функция (площадь
криволинейной трапеции увеличивается
с увеличением
![]() ),
то
),
то
![]() ,
и неравенства (2) можно записать в виде
,
и неравенства (2) можно записать в виде
![]() ,
или
,
или
![]() .
Но это означает, что
.
Но это означает, что
![]() .
.
Так как
![]() - произвольная точка интервала
- произвольная точка интервала
![]() ,
то утверждение
,
то утверждение
![]() доказано для всех точек этого интервала.
доказано для всех точек этого интервала.
Для точек
![]() и
и
![]() доказательство аналогично, но придется
рассматривать соответственно
доказательство аналогично, но придется
рассматривать соответственно
![]() и
и
![]() (то есть, правую и левую производные).
Таким образом, доказано, что для любого
(то есть, правую и левую производные).
Таким образом, доказано, что для любого
![]() из интервала
из интервала
![]() выполняется равенство
выполняется равенство
![]() ,
то есть
,
то есть
![]() является первообразной для функции
является первообразной для функции
![]() на
на
![]() .
.
Существуют и другие доказательства, в
частности такие, где рассматривается
только случай, когда функция возрастает
(или убывает), а для вычисления площади
криволинейной трапеции делят отрезок
![]() на промежутки монотонности функции
на промежутки монотонности функции
![]() .
.
Приведенный здесь способ носит более общий характер и удобен тем, что легко переносится на вычисление объема.
Учитывая относительную сложность доказательства, можно рекомендовать его для сильных учеников.
Выведем теперь формулу площади
криволинейной трапеции. Как одна из
первообразных функции
![]() функция
функция
![]() выражается через любую другую первообразную
этой функции
выражается через любую другую первообразную
этой функции
![]() по формуле
по формуле
![]() .
.
Найдем постоянную
![]() ,
используя то, что
,
используя то, что
![]() .
.
Отсюда
![]() .
Как выяснено ранее,
.
Как выяснено ранее,
![]() - это площадь данной криволинейной
трапеции. Получили формулу
- это площадь данной криволинейной
трапеции. Получили формулу
![]() ,
где
,
где
![]() .
.
Примеры. Вычислить площадь фигуры, ограниченной следующими линиями, уравнения которых заданы:
Во всех этих примерах значения
![]() и
и
![]() даны в условии задачи, поэтому площадь
вычисляется путем прямого применения
формулы.
даны в условии задачи, поэтому площадь
вычисляется путем прямого применения
формулы.
Имея в распоряжении знак неопределенного
интеграла, можно было бы несколько
короче записать решение задач. Например,
вместо записи «Одна из первообразных
функции
![]() есть
есть
![]() »
появится запись:
»
появится запись:
![]() .
.
Поставим задачу вычислить объем тела,
у которого известна площадь любого
сечения, перпендикулярного некоторой
оси
![]() .
Пусть тело располагается при этом между
плоскостями, перпендикулярными оси и
проведенными через точки
.
Пусть тело располагается при этом между
плоскостями, перпендикулярными оси и
проведенными через точки
![]() и
и
![]() на ней. Обозначим площадь сечения
на ней. Обозначим площадь сечения
![]() и будем рассматривать только случай,
когда функция
и будем рассматривать только случай,
когда функция
![]() (площадь сечения, проведенного через
точку
(площадь сечения, проведенного через
точку
![]() )
непрерывна на
)
непрерывна на
![]() .
Наряду с этой функцией будем рассматривать
функцию
.
Наряду с этой функцией будем рассматривать
функцию
![]() ,
где
,
где
![]() - объем части тела, отсекаемой плоскостью,
проведенной через точку
- объем части тела, отсекаемой плоскостью,
проведенной через точку
![]() на оси
на оси
![]() .
.
Пусть сечения тела таковы, что из любых
двух сечений тела плоскостью,
перпендикулярной оси
![]() ,
одно проектируется внутрь другого или
с ним совпадает.
,
одно проектируется внутрь другого или
с ним совпадает.
Докажем, что при этих условиях
![]() при
при
![]() .
.
Ход рассуждений будет точно таким же, как при выводе формулы площади криволинейной трапеции.
Найдем производную функции
![]() в точке
в точке
![]() .
Функция
.
Функция
![]() непрерывна, поэтому, каково бы ни было
положительное число
непрерывна, поэтому, каково бы ни было
положительное число
![]() ,
найдется такое положительное число
,
найдется такое положительное число
![]() ,
что для всех
,
что для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
выполняется условие
,
выполняется условие
![]() .
.
Если выбрать
![]() так, что
так, что
![]() ,
то для всех
,
то для всех
![]() ,
таких, что
,
таких, что
![]() при
при
![]() или
или
![]() при
при
![]() выполняется неравенство
выполняется неравенство
![]() ,
или
,
или
![]() .
.
Поэтому слой тела, отсекаемый плоскостями,
проведенными через точки
![]() и
и
![]() ,
заключен внутри прямого цилиндра с
площадью основания
,
заключен внутри прямого цилиндра с
площадью основания
![]() и высотой
и высотой
![]() и содержит в себе цилиндр с площадью
основания
и содержит в себе цилиндр с площадью
основания
![]() и высотой
и высотой
![]() .
Значит, приращение объема
.
Значит, приращение объема
![]() по модулю заключено между объемами этих
цилиндров:
по модулю заключено между объемами этих
цилиндров:
![]() .
Отсюда, так как
.
Отсюда, так как
![]() - возрастающая функция, то есть,
- возрастающая функция, то есть,
![]() и
и
![]() имеют одинаковые знаки, можно записать
имеют одинаковые знаки, можно записать
![]() ,
что означает
,
что означает
![]() ,
или
,
или
![]() ,
то есть,
,
то есть,
![]() .
.
Итак, для всех точек интервала
![]()
![]() ;
;
![]() - непрерывная на отрезке
- непрерывная на отрезке
![]() функция, то есть,
функция, то есть,
![]() - первообразная функция для
- первообразная функция для
![]() на отрезке
на отрезке
![]() (можно воспользоваться правой и левой
производной соответственно в точках
(можно воспользоваться правой и левой
производной соответственно в точках
![]() и
и
![]() ).
).
После этого можно провести те же
рассуждения, что и при выводе формулы
для площади криволинейной трапеции, а
именно
![]() выразить через любую первообразную
функции
выразить через любую первообразную
функции
![]() как
как
![]() ,
найти
,
найти
![]() и так далее.
и так далее.
Получим формулу
![]() где
где
![]() .
.
Формулу можно применить для вычисления
объемов большинства тел, которые
изучаются в курсе геометрии (пирамида,
конус, шар), и для решения задач на
вычисление объемов тел, полученных
вращением вокруг оси
![]() графика функции
графика функции
![]() .
Выбор задач ограничивается только
запасом формул интегрирования, который
имеется в распоряжении учащихся.
.
Выбор задач ограничивается только
запасом формул интегрирования, который
имеется в распоряжении учащихся.
