
Лабораторные работы / Лаб. 2 - Динамический режим
.docРоссийский химико-технологический университет им. Д.И.Менделеева
Кафедра
информатики и компьютерного проектирования
Лабораторная работа №2
«Моделирование динамических режимов простых гидравлических систем».
Вариант 15
|
Вывыполнил |
|
Прпроверил: |
Москва 2010 г.
Допущения:
-
Все параметры зависят от времени. (
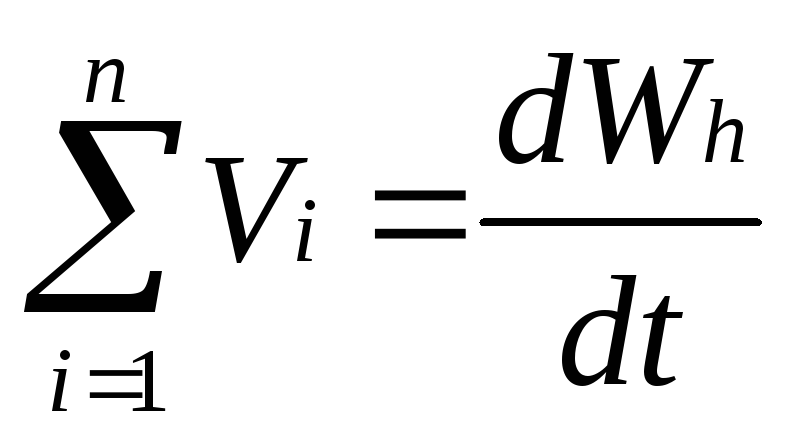 )
) -
Модель описывает только движение потока жидкости, без учета других элементарных процессов.
-
На всех участках трубопровода сопротивлением потока жидкости пренебрегаем.
-
Считаем плотность жидкости постоянной. (
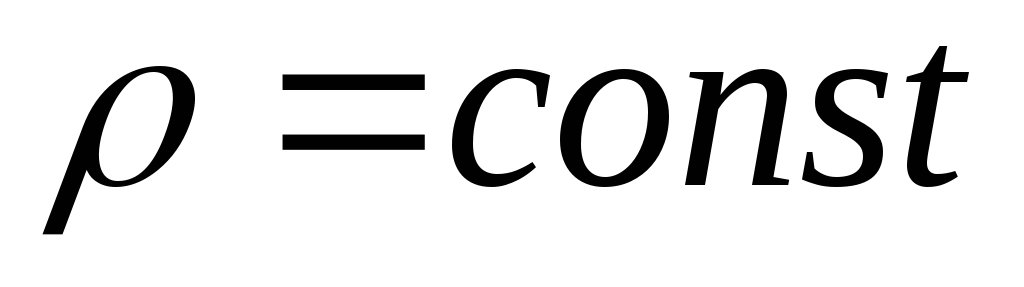 )
) -
Рассматриваем изотермический режим для газа. (T=const)
-
Система включает только клапаны с постоянными коэффициентами пропускной способности и закрытые емкости, давление газа в которых подчиняется идеальным законам. (
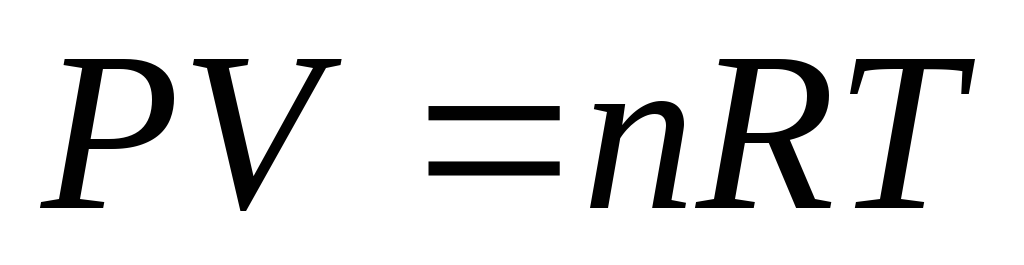 ,
К=const)
,
К=const)
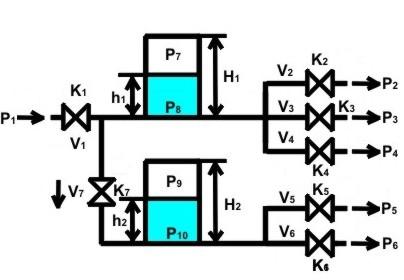
Дано:
![]()
![]()

Уравнения движения жидкости через клапаны:
для расчета давления газа в закрытой емкости.
из
![]() при T=const
при T=const
для расчета давления жидкости на дне емкости.
т.к. все параметры зависят от времени:
![]()
![]() учитывая
учитывая
![]()
Начальные условия для решения дифференциальных уравнений:
15.
![]()

|
№ |
h1 |
|
h2 |
|
P7 |
P8 |
P9 |
P10 |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
N |
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|||||
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|||||
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|||||
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|||||
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|||||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1(14) |
|||||
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f2(15) |
|||||
|
14 |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||
|
15 |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||
Принимаем h1 и h2 за неизвестные,
тогда:
![]()
![]()








![]()



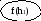
























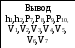



![]()






























Расчетные исследования модели:
необходимо провести анализ изменения высот жидкости в емкостях в зависимости от времени:
h1, h2 = f(t)
Компьютерная программа основана на применении:
Метод Эйлера.
Основан на разбитии
отрезка интегрирования на n
равных частей для дифференциального
уравнение y′
= f (x,
y)
, удовлетворяющего начальному условию
y(x0
) =
y0.
Величина шага интегрирования будет
равна
![]() .
Значение
функции y1
в точке x1
можно
определить как точку пересечения
касательной проведенной к функции
.
Значение
функции y1
в точке x1
можно
определить как точку пересечения
касательной проведенной к функции
![]() в точке (х0,y0)
с вертикальной прямой проходящей через
точку х1.
в точке (х0,y0)
с вертикальной прямой проходящей через
точку х1.
Тангенс угла
наклона касательной есть значение
производной в точке (х0,y0)
и задается
правой частью дифференциального
уравнения, т.е.
![]() .
.
С
другой стороны из геометрического
представления метода можно записать
![]() .
.
Следовательно
![]() .
.
Решение
будет заключаться в последовательном
применении формул:
![]()
Модифицированный метод Эйлера.
Определяем точку
![]() и вычисляем значение функции в этой
точке
и вычисляем значение функции в этой
точке
![]() .
.
Значение функции
y1
в
точке x1
определяем,
как точку пересечения касательной,
вычисленной в точке
![]() и проведенной
к функции y
= y(x)
в точке (x0,y0),
с вертикальной прямой проходящей через
точку x1.
и проведенной
к функции y
= y(x)
в точке (x0,y0),
с вертикальной прямой проходящей через
точку x1.
Произвольную
точку определим:
![]()
Вывод:
Мы проанализировали изменения высот жидкости в двух емкостях с S=1м2 в зависимости от времени t при динамическом режиме в простой гидравлической системе, приняв 6 основных допущений. Выяснили, что при входящем давления P1 =4Мпа и выходных давлений P2-P6 =1;0,2;0,3;0,3;0,5 и постоянных, одинаковых коэффициентах пропускной 0,01 высоты заполнения емкостей h1 ,h2 возрастают.
Для анализа была составлена система уравнений математического описания по заданной схеме трубопровода, информационная матрица и блок-схема алгоритма решения. По ней была модифицирована программа решения, основанная на решении дифференциальных уравнений методом Эйлера.


 +
+
 +
+
 +
+
 +
+
 +
+
 +
+
 +
+
 +
+

 +
+
 +
+

 +
+
 +
+


 +
+