Слайды для проведения занятия

Слайд 1

Тема № 11 Плотность вероятности. Числовые характеристики. Моменты случайных величин

Учебные и воспитательные цели:

1. Дать представление о методах определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности распределения.

Учебные вопросы:

1. Плотность распределения непрерывной случайной величины для определения вероятности попадания случайной величины на интервал.

2. Числовые характеристики непрерывных случайных величин.

Слайд 2

Определение вероятности попадания непрерывной случайной величины Х на участок (а;b) по известной плотности распределения:

f(х)

f(b)

f(а)

а b х

Слайд 3

Величина f(x)dx называется элементом вероятности - вероятность попадания случайной величины Х на элементарный участок dх, прилежащий к точке х:

Функция распределения случайной величины Х по известной плотности распределения может быть найдена, как интеграл от плотности распределения в интервале от - до х.

Интегральная формула полной вероятности:

Интегральная формула Бейеса:

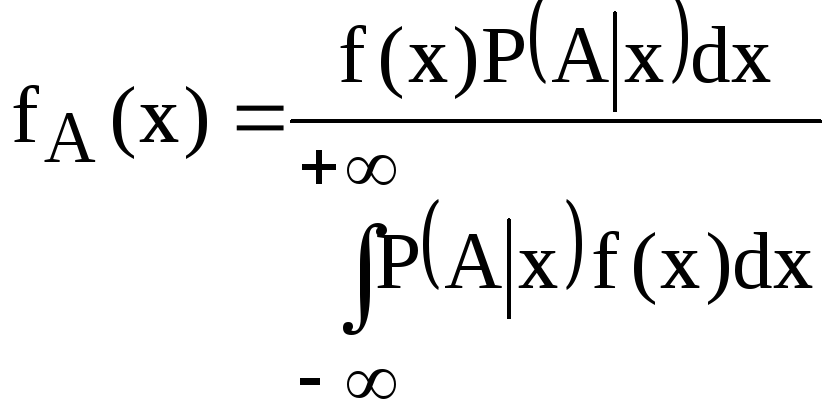
Слайд 4

Задание на самостоятельную работу

Изучить:

• Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с. – стр. 84-103

• Вентцель Е.С., Овчаров Л.А.. Теория вероятностей и ее инженерные приложения. Учебное пособие. Издание третье, переработанное и дополненное. – М.: «Академия», 2003 г. – 464 с. – стр. 96-116

• Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное.-М.:Высшая школа», 2004 г. – 480 с.- стр.75-99.