Слайды для проведения занятия

Слайд 1

Тема № 7 Основные законы распределения дискретных случайных величин. Интегральная теорема Лапласа

Учебные и воспитательные цели:

1. Изучить методику определения вероятности попадания случайной величины на интервал с использованием приведенной табличной функции распределения, приведенной табличной функции плотности распределения, приведенной табличной функции Лапласа.

Учебные вопросы:

1. Определение вероятности попадания случайной величины на интервал с использованием приведенной табличной функции распределения, приведенной табличной функции плотности распределения, приведенной табличной функции Лапласа.

Слайд 2

Пример 1: Определить вероятность попадания при одном выстреле в полосу, глубиной 10 м, расположенную перпендикулярно направлению стрельбы, если центр рассеивания снарядов находится в 10 м дальше центра полосы полосы. Срединное отклонение рассеивания снарядов по дальности равно 15 м (Вд=15) (рис. 4)

ЦЦ

ЦРС

С

10 м

Направление

стрельбы

10 м

Слайд 3

1.1 Определение вероятности попадания случайной величины х с использованием приведенной табличной функции распределения

Приведенная табличная функция распределения имеет вид (Таблица 1 Приложения к Практикуму):

,где

F(x)

1

0,5

х

Слайд 4

1.2 Определение вероятности попадания случайной величины на заданный интервал с использованием табличной функции плотности распределения

Приведенная табличная функция плотности распределения (Таблица 2 Приложения к Практикуму)

,где.

где

х

х_ср

Слайд 5

1.3Определение вероятности попадания случайной величины на заданный интервал с использованием таблиц приведенной функции Лапласа

Приведенная функция Лапласа (Таблица 3 Приложения к Практикуму)

, где .

Вероятность попадания случайной величины на заданный интервал с использованием приведенной функции Лапласа определяется из выражения:

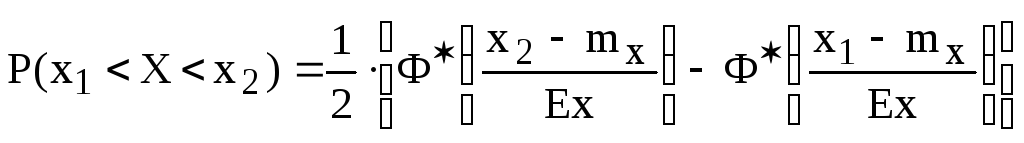
Свойства табличной функции Лапласа.

1. Функция Лапласа является неотрицательной функцией:

.

2. Табличная функция Лапласа есть нечётная функция:

Слайд 6

Задание на самостоятельную работу

Изучить:

1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с., стр. 222-227

2. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное.-М.:Высшая школа», 2004 г. – 480 с. стр. 116-123.