Теория вероятностей..

Определение 1.

Событием называется всякий факт, который может произойти или не произойти в результате опыта.

Определение 2.

События называются несовместными, если появление одного из них исключает появление других.

Определение 3.

Полной группой событий называется совокупность всех возможных результатов опыта.

Определение 4

События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.

Классификация событий: Невозможное. Достоверное.Случайное.

Классическое определение вероятностей. Вероятностью события А называется отношение числа благоприятствующих этому событию элементарных исходов (m) к общему числу возможных исходов (n):

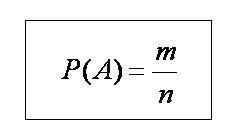
Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А.

Основные свойства вероятности события.

1. Вероятность достоверного события равна единице

2. Вероятность невозможного события равна нулю.

3. Вероятность любого события – есть положительное число, заключенное между нулем и единицей.

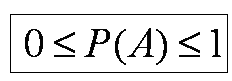
Операции над событиями.

Определение 1. Объединением или суммой событий А и В называется событие С, которое означает появление хотя бы одного из событий А или В

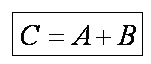
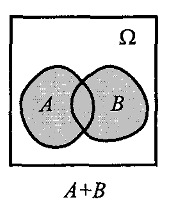
Определение. 2 Пересечением или произведением событий А и В называется событие С, которое заключается в осуществлении всех событий А и В

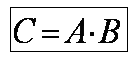
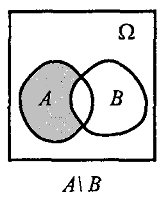
Определение 3. Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.

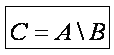
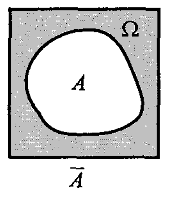
Определение 4. Дополнительным или противоположным к событию А называется событие , означающее, что событие А не происходит.

Свойства вероятности.

Теорема (сложения вероятностей несовместных событий). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

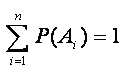
Следствие 2: Сумма вероятностей противоположных событий равна единице.

Теорема (сложения вероятностей совместных событий). Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Определение 1. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Определение 2. Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В.

Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

Также можно записать:

Если события независимые, то , и теорема умножения вероятностей принимает вид: