
- •15-------
- •21. Непрерывность функции на отрезке. Свойства функций, непрерывных на отрезке
- •Тригонометрическая форма комплексного числа
- •Показательная форма комплексного числа
- •Необходимое условие локального экстремума:
- •Достаточное условие существования экстремума функции
- •37. Наибольшие и наименьшие значения функций одной переменной.
- •38. Область определения функции нескольких переменных.
- •39. Предел функций нескольких переменных.
- •40. Приращения нескольких функций.
- •41. Локальный экстремум нескольких функций.
39. Предел функций нескольких переменных.
Общее
определение базы предела и предела
функции по данной базе. Пусть функция ![]() имеет
область определения
имеет
область определения ![]() .
.
Определение 7.8 Базой ![]() называется
такой набор множеств
называется
такой набор множеств ![]() ,
называемых окончаниями
базы,
что, во-первых, все
,
называемых окончаниями
базы,
что, во-первых, все ![]() не
пусты и, во-вторых, если
не
пусты и, во-вторых, если ![]() ,
то найдётся такое окончание
,
то найдётся такое окончание ![]() ,
что
,
что ![]() .
.
Определение 7.9
Пусть функция ![]() такова,
что её область определения содержит
целиком некоторое окончание базы
такова,
что её область определения содержит
целиком некоторое окончание базы ![]() .
Число
.
Число ![]() называется пределом функции
называется пределом функции ![]() по
базе
по
базе ![]() ,
если для любого, сколь угодно малого,
числа
,
если для любого, сколь угодно малого,
числа ![]() найдётся
такое окончание
найдётся
такое окончание ![]() базы
базы ![]() ,
что при всех
,
что при всех ![]() выполняется
неравенство
выполняется
неравенство ![]() .
Число
.
Число ![]() обозначается
тогда
обозначается
тогда
![]()
Точки
разрыва:Точка ![]() ,
в которой нарушено хотя бы одно из трех
условий непрерывности
функции,
а именно:
,
в которой нарушено хотя бы одно из трех
условий непрерывности
функции,
а именно:
функция
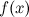 определена
в точке и ее окрестности;
определена
в точке и ее окрестности;существует конечный предел функции
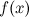 в
точке
в
точке  ;
;это предел равен значению функции в точке
 ,
т.е.
,
т.е. 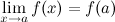
называется точкой разрыва функции.
Если
в точке ![]() существуют
конечные пределы
существуют
конечные пределы ![]() и
и ![]() ,
такие, что
,
такие, что ![]() ,
то точка
,
то точка ![]() называется точкой
разрыва первого рода.
называется точкой
разрыва первого рода.
Если
хотя б один из пределов ![]() или
или ![]() не
существует или равен бесконечности, то
точка
не
существует или равен бесконечности, то
точка ![]() называется точкой
разрыва второго рода.
называется точкой
разрыва второго рода.
40. Приращения нескольких функций.
Формула конечных приращений
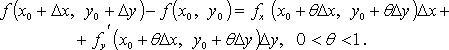
Пусть
задана функция ![]() .
Если аргументу
.
Если аргументу ![]() сообщить
приращение
сообщить
приращение ![]() ,
а аргументу
,
а аргументу ![]() –
приращение
–
приращение ![]() ,
то функция
,
то функция ![]() получит
приращение
получит
приращение ![]() ,
которое называется полным
приращением функции и
определяется формулой:
,
которое называется полным
приращением функции и
определяется формулой: ![]() .
.
Функция ![]() ,
полное приращение
,
полное приращение ![]() которой
в данной точке может быть представлено
в виде суммы двух слагаемых (выражения,
линейного относительно
которой
в данной точке может быть представлено
в виде суммы двух слагаемых (выражения,
линейного относительно ![]() и
и ![]() ,
и величины бесконечно малой высшего
порядка относительно
,
и величины бесконечно малой высшего
порядка относительно 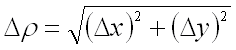 ):
):
Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.
41. Локальный экстремум нескольких функций.
Опр:
Пусть дана функция n-переменных ![]()
Пусть
дана точка M0 с
координатами ![]() ,
точкаM0 называется
локальным max(min)
если окр точки M0 : x окр справедливо
,
точкаM0 называется
локальным max(min)
если окр точки M0 : x окр справедливо![]()
( x окр ![]() ),окр называется
множество
),окр называется
множество ![]() (вn мерном
пространстве).
(вn мерном
пространстве).
![]()
Опр: локального экстремума. Точка локального max или min называются точкой экстремума.
Опр: стационарной
точки. Если
функция ![]() дифференцируема
в точкеM0 то
необходимым условием существования
экстремума в этой точке является
требование ее стационарности:
дифференцируема
в точкеM0 то
необходимым условием существования
экстремума в этой точке является
требование ее стационарности:
(![]()
![]() ,
если
,
если![]() )
)
Стационарная точка – точка где все частные производные по всем аргументам равны 0.
 Д-во: Зафиксируем
все переменные оставив только x1,
Д-во: Зафиксируем
все переменные оставив только x1, ![]()
фиксируя любую другую переменную получаем тоже самое.
Опр: Необходимое условие экстремума.
В точке экстремума функции n-переменных дифференциал обращается в ноль.
|
| ||
|
|
| |
Если
локальный экстремум ![]() ,
если
,
если![]()
![]() -
независимы
-
независимы
![]()
