Необходимое условие локального экстремума:

Если функция имеет в точке  локальный экстремум, то либо производная равна нулю  , либо не существует.

Точки которые удовлетворяют выписанным выше требованиям называюткритическими точками.

Однако в каждой критической точке функция имеет экстремум. Ответ на вопрос: будет критическая точка точкой экстремума дает следующая теорема.

Достаточное условие существования экстремума функции

Теорема І. Пусть функция непрерывна в некотором интервале, содержащем критическую точку  и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки ).

Тогда для точки функция имеет максимум, если для аргументов  выполняется условие, что производная больше нуля , а для  условие - производная меньше нуля .

Если же для производная меньше нуля , а для больше нуля , то для точки функция имеет минимум.

Теорема ІІ. Пусть функция дважды дифференцируема в окрестности точки и производная равна нулю . Тогда в точке функция имеет локальный максимум, если вторая производная меньше нуля   и локальный минимум, если наоборот .

Если же вторая производная равна нулю , то точка может и не быть точкой экстремума.

35. Выпуклость функции. Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.

Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.

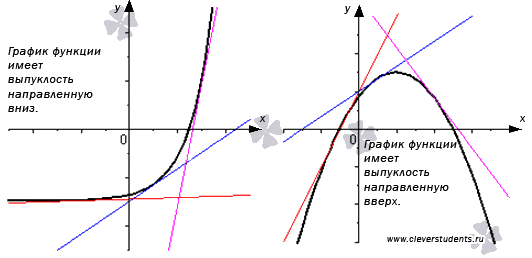
Точка называется точкой перегиба графика функции y=f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости. Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.

36. Схема исследования функции.

1. Область определения 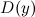и область допустимых значений 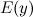функции.

2. Четность, нечетность функции.

3. Точки пересечения с осями.

4. Асимптоты функции.

5. Экстремумы и интервалы монотонности.

6. Точки перегиба и промежутки выпуклости, вогнутости.

7. Сводная таблица.

При построении графика функции необходимо провести ее предварительное исследование.

37. Наибольшие и наименьшие значения функций одной переменной.

Наибольшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Наименьшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

38. Область определения функции нескольких переменных.

Определение. Переменная  называется функцией двух переменных  и , если:

1) задано множество  пар численных значений  и ;

2) задан закон, по которому каждой паре чисел  из этого множества соответствует единственное численное значение.

При этом переменные  и  называются аргументами или независимыми переменными. Обозначения функций двух переменных аналогичны обозначениям функций одной переменной:

, , ,  и т.д.

При нахождении частного значения  функции , которое она принимает при заданных значениях аргументов  и , пишут 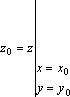 или .

Определение. Множество  всех пар значений аргументов данной функции двух переменных называется областью определения этой функции.

Например, областью определения функции  является множество, для которого . Множество  таких точек образует внутренность круга с центром в начале координат и радиусом, равным единице.

Графиком функции двух переменных в прямоугольной декартовой системе координат в пространстве является в общем случае поверхность.

Линией уровня функции  называется линия  на плоскости , в точках которой функция сохраняет постоянное значение .

На числовой оси окрестность точки – любой интервал (открытый промежуток), содержащий данную точку. В частности открытый (не содержащий границ) промежуток (а – δ; а + δ) с центром в точке а называется δ-окрестностью точки а (положительное число δ – радиус δ-окрестности).