16. Метод допускаемых напряжений.

Основой метода допускаемых напряжений является предположение, что критерием надежности конструкции будет выполнение следующего условия прочности: ,

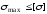где 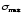- наибольшее рабочее напряжение, возникающее в одной из точек опасного сечения и определяемое расчетом; 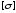- допускаемое (предельное) для данного материала напряжение, получаемое на основании экспериментальных исследований. Допускаемое напряжение определяется по формуле: ,

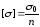где 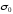- опасное напряжение (предел текучести, временное сопротивление (предел прочности)); n-коэффициент запаса прочности.

Условие прочности для центрально растянутого (сжатого) элемента будет иметь вид: , , ,

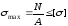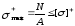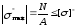где ,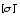- допускаемые напряжения при растяжении и сжатии.

17. Метод предельных состояний.

Предельным считается состояние, при котором конструкция перестает удовлетворять эксплуатационным требованиям или требованиям, предъявляемым в процессе возведения здания или сооружения.

Различают две группы предельных состояний:

первая - непригодность к эксплуатации по причине потери несущей способности;

вторая - непригодность к нормальной эксплуатации в соответствии с предусмотренными технологическими или бытовыми условиями.

В правильно запроектированном сооружении не должно возникнуть ни одно из указанных предельных состояний, т. е. должна быть обеспечена его надежность.

Надежностью называется способность объекта сохранять в процессе эксплуатации качество, заложенное при проектировании.

Основное уравнение предельных состояний 1-ой группы:

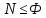, где N – самое опасное, вероятное при заданных условиях за весь срок эксплуатации усилие в конструкции, ее элементе, соединении, при самом невыгодном сочетании нагрузок и воздействий.

Ф – самая малая, вероятная при заданных условиях несущая способность той же конструкции, ее элемента, соединения.

Основное уравнение предельных состояний 2-й группы имеет вид: .

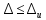 – перемещения; 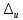– допустимые перемещения.

После перехода за предельные состояния этой группы возможна эксплуатация конструкций с ограничениями (по грузоподъемности, скорости перемещения грузов и т. п.). Подразумевается, что если устранена причина, вызвавшая переход за предельное состояние 2-й группы, и при этом конструкция не перешла за предельное состояние 1-й группы, конструкцию снова можно эксплуатировать без ограничений. 

18. Понятие напряженного состояний в точке и его виды.

Взаимодействие между частями элемента конструкции можно охарактеризовать величинами нормальных и касательных напряжений в каждой точке элемента. Эти величины зависят от направления сечения, проведенного через данную точку.

Совокупность нормальных и касательных напряжений, действующих по всем площадкам, проходящим через рассматриваемую точку, называется напряженным состоянием в этой точке.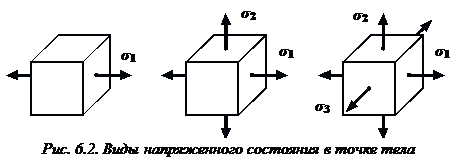

При расчетах на прочность необходимо устанавливать напряженные состояния в опасных точках конструкции.

Если через рассматриваемую точку тела нельзя провести ни одной площадки, в которой касательные и нормальные напряжения были бы равны нулю, то в этой точке имеется пространственное (трехосное) напряженное состояние. Если в одной (и только в одной) площадке, проходящей через рассматриваемую точку тела, касательные и нормальные напряжения равны нулю, то в этой точке имеется плоское (двухосное) напряженное состояние. Если касательные и нормальные напряжения равны нулю в двух площадках, проходящих через рассматриваемую точку тела, то в этой точке имеется линейное (одноосное) напряженное состояние; в таком случае касательные и нормальные напряжения равны нулю и во всех площадках, проходящих через линию пересечения указанных двух площадок.

19. Закон парности касательных напряжений.

20. Напряжения в наклонных площадках при плоском напряженном состоянии.

Разрежем элементарный параллелепипед (рис.а) наклонным сечением. Изображаем только одну плоскость. Рассматриваем элементарную треугольную призму (рис.б). Положение наклонной площадки определяется углом . Если поворот от оси x против час.стр. (см. рис.б), то >0.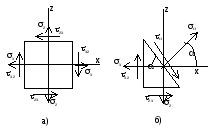

Нормальные напряжения имеют индекс, соответствующий оси их направления. Касательные напряжения, обычно, имеют два индекса: первый соответствует направлению нормали к площадке, второй — направлению самого напряжения.

Нормальное напряжение положительно, если оно растягивающее, касательное напряжение положительно, если оно стремится повернуть рассматриваемую часть элемента относительно внутренней точки по часовой стрелке.

Напряжения на наклонной площадке:

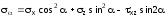
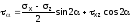
или

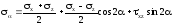
21. Главные напряжения.

При расчете инженерных конструкций нет необходимости определять напряжения во всех площадках, проходящих через данную точку; достаточно знать экстремальные (т.е. максимальные и минимальные) их значения.

Максимальные и минимальные нормальные напряжения называются главными напряжениями, а площадки, по которым они действуют, - главными площадками.

Различают три вида напряженного состояния:

1) линейное напряженное состояние — растяжение (сжатие) в одном направлении;

2) плоское напряженное состояние — растяжение (сжатие) по двум направлениям;

3) объемное напряженное состояние — растяжение (сжатие) по трем взаимно перпендикулярным направлениям.

Рассматривают бесконечно малый параллелепипед (кубик). На его гранях могут быть нормальные  и касательные  напряжения. При изменении положения "кубика" напряжения меняются.

На площадках, где действуют экстремальные для точки нормальные напряжения, касательные напряжения равны нулю. Такие площадки называются главными, а соответствующие им нормальные напряжения- главными напряжениями в точке.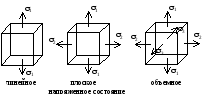

Главные напряжения обозначают: ₁, ₂, ₃ и ₁> ₂> ₃

22. Экстремальные касательные напряжения.

23. Понятие о траекториях главных напряжений.

Наглядное представление о потоке внутренних сил в нагруженном теле дают траектории главных напряжений: так называется линия, в каждой точке которой касательная совпадает с направлением главного напряжения в этой точке.

При простом растяжении бруса траекториями главных напряжений являются прямые, параллельные и перпендикулярные его оси. Если во всех точках скручиваемого стержня наметим направление главных напряжений, то на поверхности получим сетку взаимно ортогональных кривых, пересекающих образующие под углом 45 град.,- траектории главных сжимающих и растягивающих напряжений. Прямоугольный элемент, выделяемый траекториями, испытывает растяжение- сжатие в перпендикулярных направлениях, а касательные напряжения на его гранях отсутствуют.