§8 Линейные операторы. Собственные векторы и собственные значения линейного оператора

Говоря о применении элементов линейной алгебры в экономике, мы уже упомянули (§1), что основная часть экономических данных хранится и обрабатывается в матричной форме. Также необходимо упомянуть, что математическая модель Леонтьева многоотраслевой экономики(которая решает задачу расчета связи между отраслями через выпуск и потребление продукции разного вида) основана на алгебре матриц. А в качестве примера математической модели экономического процесса, приводящейся к понятиюсобственного вектора и собственного значения матрицы, можно взятьмодель международной торговли(которая анализирует процесс взаимных закупок товаров)⁷.

В этом параграфе даются краткие сведения для знакомства с разделом матричной алгебры. Одно из фундаментальных понятий матричной алгебры – понятие линейного оператора.

Определение 1.8.Если в пространствеRⁿзадан закон (правило), по которому каждому векторухRⁿставится в соответствие определённый векторуRⁿ, то говорят, что заданоператорА(х).

Вектор у=А(х) называетсяобразомвекторах, а сам векторх–прообразомвекторау.

Примером такого оператора может служить умножение каждого вектора на его длину.

Определение 2.8.Оператор называетсялинейным, если для любых векторовх,уRⁿи любого действительного числаλвыполняются равенства:

А(х+у) =А(х)+А(у),

А(λх) =λА(х).

Определение 3.8.Линейный операторЕназываетсятождественным, если он преобразует любой векторхв самого себя:Е(х) =х.

Определение 4.8.Линейный операторΟназываетсянулевым, если он преобразует любой векторхв нулевой:Ο(х) =.

Разъясним связь между известным нам понятием “матрица” и новым понятием “оператор”.

Пусть задан линейный оператор А(х) и некоторый фиксированный базисе₁,е₂, …,е_n. Так как образы базисных векторовА(е₁),А(е₂), …,А(е_n) – векторы пространстваRⁿ, то каждый из них можно разложить единственным способом по векторам базиса:

Определение 5.8.

Матрицу называютматрицей оператораА(х) в базисее₁,е₂, …,е_n. Столбцы этой матрицы составлены из коэффициентов в формулах преобразования базисных векторов.

□

Пусть линейный оператор в R³определяется равенством

А(х) = (0,х₂х₃, 3х₁х₂+х₃).

Найдем матрицу оператора в определённом базисе.

Возьмём в пространстве R³канонический базис:е₁≡(1, 0, 0);е₂≡(0, 1, 0);е₃≡(0, 0, 1). Преобразуем согласно заданному правилу базисные векторы:

Следовательно, – матрица линейного оператораА(х) в каноническом базисе.

■

Пользуясь определением матрицы линейного оператора, самостоятельно убедитесь, что тождественный оператор будет иметь своей матрицей единичную, а нулевой оператор – нулевую.

Рассмотреть на примере пространства R³, гдеЕ(х) = (х₁,х₂,х₃), аΟ(х) = (0, 0, 0).

Связь между вектором хи его образомуможет быть представлена в матричном виде так:

Y = АX, (1.8)

где А– матрица линейного оператора,

а – столбцы координат векторовхиу.

□

Пусть в пространстве R³с базисоме₁,е₂,е₃действует линейный оператор, заданный матрицей.

Найдем координаты образа увекторах=2е₁+е₂–3е₃.

Вектор х=2е₁+е₂–3е₃в базисее₁,е₂,е₃имеет координаты (2, 1, –3). Запишем координаты векторахв столбец и воспользуемся упомянутой выше формулой (1.8):

.

Вектор у=(–5, 7, 0) – образ векторахв базисее₁,е₂,е₃.

■

В дальнейшем изложении нам следовало бы определить следующие действия над линейными операторами: сложение линейных операторов,умножение линейного оператора на число,умножение линейных операторов,нахождение обратного линейного оператора. Так как линейный оператор однозначно представляется своей матрицей в некотором фиксированном базисе, то все эти операции хорошо нам известны по §§1, 3 как операции над матрицами, поэтому останавливаться на них не будем, а перейдём непосредственно к понятиям, представляющим экономический интерес.

Определение 6.8.Ненулевой векторхназываетсясобственным векторомлинейного оператораА(х), если найдется такое числоλ, что

А(х) =λх

Число λназываетсясобственным(характеристическим)значением(числом) оператораА(х), соответствующим векторух.

Из определения следует, что собственный вектор под действием линейного оператора просто умножается на некоторое число (говорят: переходит в вектор, коллинеарный самому себе).

Если – матрица линейного оператораА(х), аХ– столбец координат векторах, то равенствоА(х)=λх можно записатьв матричной форме:

АХ = λХ .

□

Покажем, что для линейного оператора с матрицей в некотором базисе собственными значениями являются числаλ₁=1,λ₂=13 с соответствующими им собственными векторамих⁽¹⁾ = (1;1),х⁽²⁾ = (1; 2).

Действительно,

■

Равенство АХ=λХв развёрнутом виде записывается так:

Перепишем систему таким образом, чтобы в правых частях уравнений были нули:

(2.8)

Полученная однородная система всегда имеет нулевое решение. Для существования ненулевого решениянеобходимо и достаточно, чтобы ееопределитель равнялся нулю:

. (3.8)

Определение 7.8.Определительdet(А–λЕ) является многочленомn-й степени относительноλи называетсяхарактеристическим многочленомлинейного оператораА(х), а само уравнениеdet(А–λЕ)=0 –характеристи-ческим уравнением.

Запишем алгоритм нахождения собственных векторов и собственных значенийлинейного оператора, заданного своей матрицей.

1. Составляем характеристическое уравнение(3.8)и решаем его.Собственными значениями будут корниλ₁,λ₂, … ,λ_nхарактеристического уравнения.

Характеристическое уравнение (если рассматривать его как произвольное уравнениеn-й степени) не всегда имеетnразличных корней, тогда различными будут не все собственные значения. Может случиться так, что действительных корней не будет вообще, тогда не будет и действительных собственных значений.

2. Определив набор чиселλ₁,λ₂, … ,λ_n,для каждого из них находим соответствующийсобственный вектор как решение однородной системы(2.8).

Поопределению 6.8х, тогда однородная система (2.8) будет иметь бесконечное множество решений. Следовательно, каждому собственному значению соответствует не единственный собственный вектор, а бесконечное множество.

□

Найдем собственные значения и собственные векторы оператора, заданного в некотором базисе матрицей .

1. Для этого составим и решим характеристическое уравнение:

Откуда λ₁ = –2,λ₂ = 5 – собственные значения.

2. Найдем собственный вектор х⁽¹⁾=(х₁,х₂), соответствующий собственному значениюλ₁ = –2. Запишем равенство АХ=λХв развернутом виде:

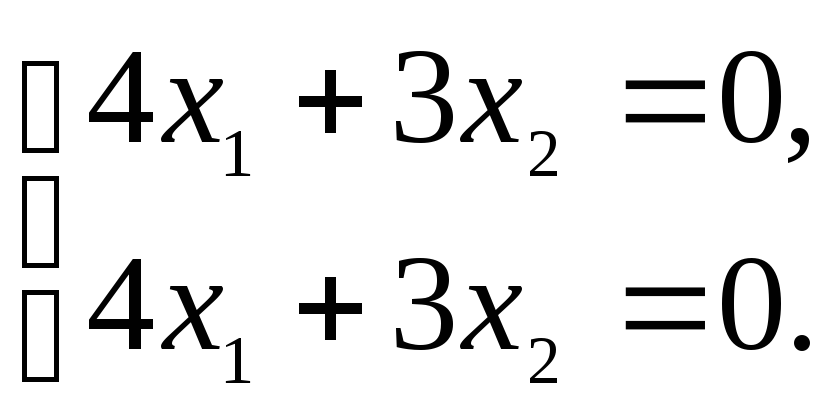
Полагая х₂ = с₁, найдем .

Вектор при любом действительномс₁≠0 есть собственный вектор оператора с собственным значениемλ₁= –2.

Найдем собственный вектор х⁽²⁾=(х₁,х₂), соответствующий собственному значениюλ₂ = 5. Запишем равенство АХ=λХдля данногоλ:

Полагая х₂ = с₂, найдем х₁ = с₂.

Вектор при любом действительномс₂≠0 есть собственный вектор оператора с собственным значениемλ₂= 5.

Так как с₁ис₂– произвольные числа, то формулы и описывают всю совокупность собственных векторов, соответствующих собственным значениямλ₁ и λ₂.

Ответ: λ₁= –2,;λ₂= 5,;с₁,с₂R;с₁≠0,с₂≠0.

■