
- •Тема 6. Теорема о движении центра масс. Количество движения и кинетический момент механической системы. Теорема об изменении количества движения. Теорема об изменении кинетического момента.
- •Тема 3. Обратная задача динамики
- •Тема 4. Потенциальное силовое поле. Работа потенциальной силы.
- •Тема 5. Колебательное движение материальной точки
- •Тема 6. Теорема о движении центра масс. Количество движения и кинетический момент механической системы. Теорема об изменении количества движения. Теорема об изменении кинетического момента.
- •Тема 7. Теорема об изменении кинетической энергии механической системы. Законы сохранения механической энергии и количества движения системы.
- •Тема 10. Определение скоростей точек твёрдого тела в плоском движении
- •Тема 11. Определение ускорений точек твёрдого тела в плоском движении
- •Тема 14. Определение направления ускорения Кориолиса
- •Тесты_тм_ч_1_2007
- •Тема 2. Определение момента силы
- •Тема 3. Определение направлений реакций опор конструкции (в простейших случаях); статически определяемые и статически неопределимые системы
- •4) Под углом α к горизонтали
- •4) Равна нулю
- •4) Равна нулю.
- •4) Равна нулю.
- •4) Равна нулю.
- •4) Равна нулю.
- •4) Равна нулю.
- •4) В направлении к точке в.
- •4) Равна нулю.
- •2013/2014 Учебный год
- •Тема 1. Кинематика точки. Простейшие движения твёрдого тела.
- •Ответ: 52
- •Ответ: 60
- •Тема 2. Определение мгновенного центра скоростей звена плоского механизма
- •Тема 3. Определение скоростей точек твёрдого тела в плоском движении
- •2013/2014 Учебный год
- •Тема 4. Основные понятия и законы классической механики
- •Тема 5. Прямая задача динамики
- •Тема 6. Обратная задача динамики
Тема 7. Теорема об изменении кинетической энергии механической системы. Законы сохранения механической энергии и количества движения системы.
I: 241.
S :
Стержень представляет собой шарнирно
соединённую со штативом лёгкую жёсткую
спицу с закреплёнными на ней двумя
небольшими по размерам грузами массыm каждый
(см. рис.); расстояния между точкой
крепления О и верхним грузом и между
грузами равныl.
Первоначально стержень был отклонён
горизонтально, а затем отпущен без
начальной скорости.
:
Стержень представляет собой шарнирно
соединённую со штативом лёгкую жёсткую
спицу с закреплёнными на ней двумя
небольшими по размерам грузами массыm каждый
(см. рис.); расстояния между точкой
крепления О и верхним грузом и между
грузами равныl.
Первоначально стержень был отклонён
горизонтально, а затем отпущен без
начальной скорости.
Угловая скорость ω
стержня в момент прохождения им
нижнего положения имеет видω
= Kּ![]() (g
– ускорение свободного падения).
Определить числовой коэффициент K.
(Результат вычисления округлить
до первого знака после запятой
включительно.) K = …
(g
– ускорение свободного падения).
Определить числовой коэффициент K.
(Результат вычисления округлить
до первого знака после запятой
включительно.) K = …
+: 1,1
I: 242.
S :
Прямой однородный стержень длинойl,
шарнирно соединённый со штативом,
первоначально был отклонён горизонтально,
а затем был отпущен без начальной
скорости. Угловая скоростьω
стержня в момент прохождения им
нижнего положения имеет видω
=Kּ
:
Прямой однородный стержень длинойl,
шарнирно соединённый со штативом,
первоначально был отклонён горизонтально,
а затем был отпущен без начальной
скорости. Угловая скоростьω
стержня в момент прохождения им
нижнего положения имеет видω
=Kּ![]() (g
– ускорение свободного падения;
момент инерции стержня ОА относительно
шарнира О:JО= (1/3)·m·l2).
Определить числовой коэффициент K.
(Результат вычисления округлить
до второго знака после запятой
включительно.) K
= … .
(g
– ускорение свободного падения;
момент инерции стержня ОА относительно
шарнира О:JО= (1/3)·m·l2).
Определить числовой коэффициент K.
(Результат вычисления округлить
до второго знака после запятой
включительно.) K
= … .
+:1,73
I: 243.
S :
Масса каждого из тёх звеньев шарнирного
параллелограммаОАВС(ОА, АВ, СВ)
равна 3 кг. Длина кривошипаОАравна 0,6 м. КривошипОАвращается
равномерно с угловой скоростьюω= 5 рад/с. Определить кинетическую энергиюT механизма (числовой результат
определить с точностью до первого знака
после запятой включительно);T= …
:
Масса каждого из тёх звеньев шарнирного
параллелограммаОАВС(ОА, АВ, СВ)
равна 3 кг. Длина кривошипаОАравна 0,6 м. КривошипОАвращается
равномерно с угловой скоростьюω= 5 рад/с. Определить кинетическую энергиюT механизма (числовой результат
определить с точностью до первого знака
после запятой включительно);T= …
+: 22,5
I: 244.
S :
Цилиндр 1 вращается с угловой скоростьюω= 20 рад/с.
Его момент инерции относительно оси
вращенияЈ= 2 кгּм2, радиусr
= 0,5 м. Груз 2 имеет массуm2
= 1 кг.
:
Цилиндр 1 вращается с угловой скоростьюω= 20 рад/с.
Его момент инерции относительно оси
вращенияЈ= 2 кгּм2, радиусr
= 0,5 м. Груз 2 имеет массуm2
= 1 кг.
Определить кинетическую энергию T механизма;
T = … (Дж)
+: 450
I: 245.
S :
В кривошипно-шатунном механизмеОАВ,
расположенном в горизонтальной плоскости,
кривошипОАи шатунАВ имеют
каждый массуm
и длинуl, а ползунВимеет
массуm/2.
Угловая скорость кривошипа равна ω.
:
В кривошипно-шатунном механизмеОАВ,
расположенном в горизонтальной плоскости,
кривошипОАи шатунАВ имеют
каждый массуm
и длинуl, а ползунВимеет
массуm/2.
Угловая скорость кривошипа равна ω.
Определить кинетическую энергию механизма в тот момент, когда угол α = 0. (Момент инерции стержня ОА относительно шарнира О:JО= (1/3)·m·l2).
Кинетическая энергия в тот момент имеет вид: T = Kּmּl2ּω2 . Вычислить числовой коэффициент K (результат вычисления округлить до первого знака после запятой включительно);
K= …
+: 0,3
I: 246.
S :
Сплошной однородный диск радиусаRи массыm, жёстко
скрепленный с прямолинейным стержнемАВ массыmи длиной
2ּR,
катится прямолинейно по гладкой
поверхности так, что центрО имеет
скоростьv.
:
Сплошной однородный диск радиусаRи массыm, жёстко
скрепленный с прямолинейным стержнемАВ массыmи длиной
2ּR,
катится прямолинейно по гладкой
поверхности так, что центрО имеет
скоростьv.
Определить кинетическую энергию механизма. (момент инерции стержня АВ относительно оси, проходящей через точку О перпендикулярно стержню: JО= (1/12)·m·l2)
Кинетическая энергия имеет вид: T = Kּmּv2. Вычислить числовой коэффициент K (результат вычисления округлить до первого знака после запятой включительно); K = …
+: 1,3
I: 247.
S: Мощность гидроэлектростанцииW = 73,5 МВт (мегаватт). Найти объёмный расход водыV (м3/сек), если КПД станцииη= 0,75 и плотина поднимает уровень воды на высотуh = 10 м. (g= 9,8 м/с2). (Результат вычисления округлить до целого числа.)
V = … (м3/сек)
+: 1000
I: 248.
S :В кривошипно-шатунном механизмеОАВ,
расположенном в горизонтальной плоскости,
кривошипОАи шатунАВ имеют
каждый массуm,
а ползунВимеет массуm/2.
Длина кривошипаOAравнаl, длина шатунаABравна
2ּl.
Угловая скорость кривошипа равна ω.
:В кривошипно-шатунном механизмеОАВ,
расположенном в горизонтальной плоскости,
кривошипОАи шатунАВ имеют
каждый массуm,
а ползунВимеет массуm/2.
Длина кривошипаOAравнаl, длина шатунаABравна
2ּl.
Угловая скорость кривошипа равна ω.
Определить кинетическую энергию механизма в тот момент, когда угол α = π/2. (Момент инерции однородного стержня относительно шарнира О:
JО= (1/3)·m·l2)
Кинетическая энергия в тот момент имеет вид:
T = Kּmּl2ּω2 . Вычислить числовой коэффициент K (результат вычисления округлить до первого знака после запятой включительно);
K= …
+: 0,9
I: 249.
S :
Груз В весом Р = 200 Н положен без
начальной скорости на невесомую плиту,
прикреплённую к вертикальной пружине.
После этого груз стал совершать
гармонические колебания с амплитудойA = 5 см.
:
Груз В весом Р = 200 Н положен без
начальной скорости на невесомую плиту,
прикреплённую к вертикальной пружине.
После этого груз стал совершать
гармонические колебания с амплитудойA = 5 см.
Определить максимальное значение кинетической энергии Tmax, которое может достигаться в колебательном контуре для данной механической системы.
Tmax= … (Дж).
+: 5
I: 250.
S :
Груз М поместили без начальной скорости
к середине неизогнутой балки жёсткостис = 400 Н/см.
Балка совершает поперечные колебания
с амплитудойA =
3 см.
:
Груз М поместили без начальной скорости
к середине неизогнутой балки жёсткостис = 400 Н/см.
Балка совершает поперечные колебания
с амплитудойA =
3 см.
Определить максимальное значение кинетической энергии Tmax, которое может достигаться в колебательном процессе для данной механической системы.
Tmax= … (Дж).
+: 18
I: 251.
S: Поезд массыm = 500 тонн после прекращения тяги тепловоза останавливается под действием силы тренияFтр= 0,1 МН (мега-ньютон) через времяt= 1 мин.
Вычислить величину работы силы трения (миллионов Дж) на данном промежутке пути. Aтр = … (МДж).
+: 36
I: 252.
S :
Горизонтальная трубка вращается
вокруг вертикальной осиOz,
её момент инерцииЈz= 0,075 кгּм2. ШарикMмассыm= 0,1 кг первоначально был помещён в трубке
на расстоянииl= 0,5 м от оси вращенияОz. Угловая
скорость вращения трубки была ω0= 3 рад/с. Затем шарик посредством
соответствующего устройства перемещают
до оси вращенияОz. Трением пренебречь.
:
Горизонтальная трубка вращается
вокруг вертикальной осиOz,
её момент инерцииЈz= 0,075 кгּм2. ШарикMмассыm= 0,1 кг первоначально был помещён в трубке
на расстоянииl= 0,5 м от оси вращенияОz. Угловая
скорость вращения трубки была ω0= 3 рад/с. Затем шарик посредством
соответствующего устройства перемещают
до оси вращенияОz. Трением пренебречь.
Определить величину работы A(Дж) устройства по перемещению шарика из исходного положения в конечное положение (числовой результат определить с точностью до второго знака после запятой); A= …(Дж)
+: 0,15
I: 253.
S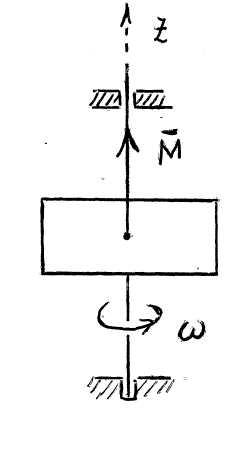 :
Тело вращается вокруг вертикальной
осиOzпод действием
пары сил с моментомМ = 16ּt
(Нּм). Приt
= 0 тело находилось в покое, а в моментt = 3 с
угловая скоростьω
= 2 рад/с.
:
Тело вращается вокруг вертикальной
осиOzпод действием
пары сил с моментомМ = 16ּt
(Нּм). Приt
= 0 тело находилось в покое, а в моментt = 3 с
угловая скоростьω
= 2 рад/с.
Определить кинетическую энергию вращающегося тела в момент t = 3 сек. (Результат вычисления – целое число.)
Кинетическая энергия равна = … (Дж)
+: 72
I: 254.
S :
Горизонтальная трубкаCD может
свободно вращаться вокруг вертикальной
осиAB. Её момент инерции относительно
оси вращения равенJ
= 0,7 кгּм2.
Внутри трубки на расстоянииL = 1 м;
от оси находится шарикMмассыm
= 0,5 кг (шарик считать материальной
точкой). В некоторый момент времени трубке
сообщается начальная угловая скоростьω0= 3 рад/сек. Затем шарик посредством
соответствующего устройства перемещается
в новое положение – на расстояниеb
= 0,2 м от оси вращения. Трением
пренебречь.
:
Горизонтальная трубкаCD может
свободно вращаться вокруг вертикальной
осиAB. Её момент инерции относительно
оси вращения равенJ
= 0,7 кгּм2.
Внутри трубки на расстоянииL = 1 м;
от оси находится шарикMмассыm
= 0,5 кг (шарик считать материальной
точкой). В некоторый момент времени трубке
сообщается начальная угловая скоростьω0= 3 рад/сек. Затем шарик посредством
соответствующего устройства перемещается
в новое положение – на расстояниеb
= 0,2 м от оси вращения. Трением
пренебречь.
Определить величину работы A(Дж) устройства по перемещению шарика из исходного положения в конечное положение (числовой результат определить с точностью до первого знака после запятой); A= … (Дж)
+: 3,6
I: 255.
S: Снаряд массыm= 12 кг, летевший со скоростьюv = 800 м/с, разорвался в воздухе на 240 равных по массе осколков. Разлёт осколков в системе отсчёта, связанной с первоначальным снарядом, является сферически симметричным, и скорость каждого осколка в этой системе отсчёта равнаvотн= 600 м/с.
Определить кинетическую энергию T (миллионов Дж) системы осколков относительно земли;T= …(МДж).
+: 6
I: 256.
S :
КонцыАиВ стержня длиныl
массыmдвижутся соответственно по осямОхиОу.Скорость точкиA равнаvA.
Угол наклона стержня к горизонтали в
рассматриваемый момент времени равен
60о.
(Момент инерции однородного стержня
относительно оси, проходящей через
середину стержня перпендикулярно
стержню:Jс= (1/12)·m·l2
)
:
КонцыАиВ стержня длиныl
массыmдвижутся соответственно по осямОхиОу.Скорость точкиA равнаvA.
Угол наклона стержня к горизонтали в
рассматриваемый момент времени равен
60о.
(Момент инерции однородного стержня
относительно оси, проходящей через
середину стержня перпендикулярно
стержню:Jс= (1/12)·m·l2
)
Кинетическая энергия стрежня имеет вид
T = KּmּvА2. Определить для данного момента времени числовой коэффициент K (числовой результат определить с точностью до первого знака после запятой);
K = ….
+: 0,2
I: 257.
S :
КонцыАиВ стержня длиныl
массыmдвижутся соответственно по осямОхиОу.Скорость точкиA равнаvA.
Угол наклона стержня к горизонтали в
рассматриваемый момент времени равен
45о.
(Момент инерции однородного стержня
относительно оси, проходящей через
середину стержня перпендикулярно
стержню:Jс
= (1/12)·m·l2
)
:
КонцыАиВ стержня длиныl
массыmдвижутся соответственно по осямОхиОу.Скорость точкиA равнаvA.
Угол наклона стержня к горизонтали в
рассматриваемый момент времени равен
45о.
(Момент инерции однородного стержня
относительно оси, проходящей через
середину стержня перпендикулярно
стержню:Jс
= (1/12)·m·l2
)
Кинетическая энергия стрежня имеет вид
T = KּmּvА2. Определить для данного момента времени числовой коэффициент K (числовой результат определить с точностью до первого знака после запятой);
K = ….
+: 0,3
I: 258.
S :КонцыАиВ стержня длиныl
массыmдвижутся соответственно по осямОхиОу.Скорость точкиA равнаvA.
Угол наклона стержня к горизонтали в
рассматриваемый момент времени равен
30о.
(Момент инерции однородного стержня
относительно оси, проходящей через
середину стержня перпендикулярно
стержню:Jс= (1/12)·m·l2
)
:КонцыАиВ стержня длиныl
массыmдвижутся соответственно по осямОхиОу.Скорость точкиA равнаvA.
Угол наклона стержня к горизонтали в
рассматриваемый момент времени равен
30о.
(Момент инерции однородного стержня
относительно оси, проходящей через
середину стержня перпендикулярно
стержню:Jс= (1/12)·m·l2
)
Кинетическая энергия стрежня имеет вид
T = KּmּvА2. Определить для данного момента времени числовой коэффициент K (числовой результат определить с точностью до первого знака после запятой);
K = ….
+:0,7
I: 259.
S :
Шарик массойm= 100 г подвешен на
нитке длинойl= 1 м. Шарик раскрутили
так, что он начал двигаться по окружности
в горизонтальной плоскости (см. рис.).
При этом угол, составляемый нитью с
вертикалью,α = 60о. Определить
полную работу, совершаемую при
раскручивании шарика. Ускорение
свободного падения принять равнымg= 9,81 м/с2; результат вычисления
округлить до второго знака после запятой
включительно.
:
Шарик массойm= 100 г подвешен на
нитке длинойl= 1 м. Шарик раскрутили
так, что он начал двигаться по окружности
в горизонтальной плоскости (см. рис.).
При этом угол, составляемый нитью с
вертикалью,α = 60о. Определить
полную работу, совершаемую при
раскручивании шарика. Ускорение
свободного падения принять равнымg= 9,81 м/с2; результат вычисления
округлить до второго знака после запятой
включительно.
А = …(Дж)
+: 1,23
I: 260.
S :
Дано:M,m,
уголα,
причёмM = 4ּm.
Массой блока и нитей и силой трения
пренебречь. Ускорение тела 1 выражается
соотношениемa
= Kּgּsinα.
:
Дано:M,m,
уголα,
причёмM = 4ּm.
Массой блока и нитей и силой трения
пренебречь. Ускорение тела 1 выражается
соотношениемa
= Kּgּsinα.
Числовой коэффициент K = …
+: 0,6
I: 261.
S :Дано:m1,
колесо массы m2– однородный цилиндр, причемm2
=
:Дано:m1,
колесо массы m2– однородный цилиндр, причемm2
=![]() ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием колеса и силой трения,
определить ускорение груза 1.
ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием колеса и силой трения,
определить ускорение груза 1.
Ускорение груза 1 выражается соотношением a= Kּg.
Числовой коэффициент K = …
+: 0,5
I: 262.
S :Дано:m1,
колесо массы m2– однородный цилиндр, причемm2
=
:Дано:m1,
колесо массы m2– однородный цилиндр, причемm2
=![]() ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием колеса и силой трения
в блоке, определить ускорение груза 1.
ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием колеса и силой трения
в блоке, определить ускорение груза 1.
Ускорение груза 1 выражается соотношением a= Kּg.
Числовой коэффициент K = …
+: 0,2
I: 263.
S :
Дано:m1,
уголα,
каток массы m2– однородный цилиндр, причемm2
=
:
Дано:m1,
уголα,
каток массы m2– однородный цилиндр, причемm2
=![]() ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием катка и силой трения
в блоке, определить ускорение груза 1.
ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием катка и силой трения
в блоке, определить ускорение груза 1.
Ускорение груза 1 выражается соотношением a= Kּgּsinα.
Числовой коэффициент K = …
+: 0,4
I: 264.
S :Дано: катки массыm1иm2– однородные цилиндры, уголα,
причемm2
=
:Дано: катки массыm1иm2– однородные цилиндры, уголα,
причемm2
=![]() ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием катков и силой трения
в блоке, определить ускорение центра
катка 1.
ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием катков и силой трения
в блоке, определить ускорение центра
катка 1.
Названное ускорение выражается соотношением aC1 = Kּgּsinα.
Числовой коэффициент K = …
+: 0,25
I: 265.
S :Дано: катки массыm1иm2– однородные цилиндры, уголα,
причемm2
= 2,4ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием катков и силой трения
в блоке, определить ускорение центра
катка 1.
:Дано: катки массыm1иm2– однородные цилиндры, уголα,
причемm2
= 2,4ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием катков и силой трения
в блоке, определить ускорение центра
катка 1.
Названное ускорение выражается соотношением aC1 = Kּgּsinα.
Числовой коэффициент K = …
+: 0,5
I: 266.
S :Дано: катки массыm1иm2– однородные цилиндры, уголα,
причемm2
= 0,25ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием катков и силой трения
в блоке, определить ускорение центра
катка 1.
:Дано: катки массыm1иm2– однородные цилиндры, уголα,
причемm2
= 0,25ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием катков и силой трения
в блоке, определить ускорение центра
катка 1.
Названное ускорение выражается соотношением aC1 = Kּgּsinα.
Числовой коэффициент (результат вычисления округлить до первого знака после запятой включительно) K = …
+: 0,7
I: 267.
S: С горки высотойh = 2 м и основаниемb= 5 м съезжают санки, которые останавливаются, пройдя горизонтально путьs = 35 м от основания горы.
Найти коэффициент трения, считая его одинаковым на всём пути: …
+: 0,05
I: 268.
S :Груз массыm,
опускаясь вниз, при помощи троса
перекинутого через неподвижный блок,
поднимает груз 2 тоже массыm,
прикреплённый к оси подвижного блока.
Определить ускорение груза 1. Массами
блоков и силами трения пренебречь.
:Груз массыm,
опускаясь вниз, при помощи троса
перекинутого через неподвижный блок,
поднимает груз 2 тоже массыm,
прикреплённый к оси подвижного блока.
Определить ускорение груза 1. Массами
блоков и силами трения пренебречь.
Названное ускорение выражается соотношением a1 = Kּg.
Числовой коэффициент K = …
+: 0,4
I: 269.
S :Дано: груз массыm1,
каток массыm2– однородный цилиндр, уголα,
причемm2
= 0,7ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием катка и силой трения
в блоке, определить груза 1.
:Дано: груз массыm1,
каток массыm2– однородный цилиндр, уголα,
причемm2
= 0,7ּm1.
Пренебрегая массой блока и каната, также
проскальзыванием катка и силой трения
в блоке, определить груза 1.
Названное ускорение выражается соотношением a1 = Kּgּsinα.
Числовой коэффициент (результат вычисления округлить до первого знака после запятой включительно) K = …
+: 0,5
I: 270.
S :К концу троса, намотанного на барабан,
прикреплён груз 1 массыm1.
К барабану ворота 2 радиусаrи массыm2
приложен постоянный вращающий
моментM. При этом
:К концу троса, намотанного на барабан,
прикреплён груз 1 массыm1.
К барабану ворота 2 радиусаrи массыm2
приложен постоянный вращающий
моментM. При этом
m1=m,m2= 0,5ּm.
Определить ускорение тела 1.
Названное ускорение выражается
соотношением a
= Kּ![]() .
.
Числовой коэффициент K = …
+: 0,8
