Тема 6. Теорема о движении центра масс. Количество движения и кинетический момент механической системы. Теорема об изменении количества движения. Теорема об изменении кинетического момента.

I: 201.

S: Человек массыm = 60 кг переходит с носа на корму лодки. На какое расстояние по величине |s |переместится лодка длиныl = 3 м, если её массаM = 120 кг?

| s | = … (м).

+: 1 .

I: 202.

S: Колесо радиусаR = 0,5 м и массыm = 10 кг катится со скольжением по горизонтальной прямой под действием приложенного к нему вращательного моментаM =6 Нּм. Определить ускорениеa_Cцентра массCколеса, если коэффициент трения скольжения равенf= 0,1. Ускорение свободного падения принять равнымg = 10 м/с². a_C= …

+: 1

I: 203.

S: Колесо радиусаR = 0,5 м и массыm = 10 кг скатывается с наклонной плоскости вниз. Его центр массCдвижется по законуx_C=t ²(м). Определить модуль главного вектора внешних сил |F^(e)|, действующих на колесо; |F^(e)| = … (Н).

+:20

I: 204.

S: Тело массыm = 40 г, брошенное вертикально вверх с начальной скоростьюv₀ = 30 м/с, достигло высшей тоски спустя времяt = 2,5 сек. Найти среднюю силу сопротивленияF _сопр.воздуха, действовавшую на тело во время движения. (Результат вычисления округлить до третьего знака после запятой включительно.) (g= 9,81 м/с²)F _сопр. = … (Н)

+:0,088

I: 205.

S: Тело 1 массойm= 50 кг поднимается по наклонной плоскости с помощью троса, намотанного на барабан 2 радиусаR = 0,4 м. Угловое ускорение барабанаε= 5 рад/с². Определить модуль вектора всех внешних сил вектора внешних сил |F^(e)|, действующих на тело; |F^(e)| = … (Н).

+: 100

I: 206.

S: Шкив 1 массыМ= 20 кг и радиусаR =0,4 м, вращаясь с угловой скоростьюω = 2,5 рад/с, поднимает груз 2 массыm = 10 кг. Определить модуль количества движения |Q| механизма; |Q| = … (кгּм/с).

+: 10

I: 207.

S: Мяч массыm = 150 г ударяется о гладкую стенку под угломα = 30^о к ней и отскакивает без потери скорости. Найти среднюю силуF, действующую на мяч со стороны стенки, если скорость мячаv₀ = 10 м/с, а продолжительность удара Δt = 0,1 сек.F = … (Н).

+: 15

I: 208.

S: Масса каждого из тёх звеньев шарнирного параллелограммаОАВС(ОА, АВ, СВ) равна 3 кг. Длина кривошипаОАравна 0,6 м. КривошипОАвращается равномерно с угловой скоростьюω= 5 рад/с.

Определить модуль количества движения |Q| механизма; |Q| = … (кгּм/с).

+: 18

I: 209.

S: Цилиндр 1 вращается с угловой скоростьюω= 20 рад/с. Его момент инерции относительно оси вращенияЈ= 2 кгּм², радиусr = 0,5 м. Груз 2 имеет массуm₂ = 1 кг.

Определить модуль количества движения |Q| механизма; |Q| = … (кгּм/с).

+: 10

I: 210.

S: В кривошипно-шатунном механизмеОАВ, расположенном в горизонтальной плоскости, кривошипОАи шатунАВ имеют каждый массуm = 3 кг, а ползунВимеет массуm/2 = 1,5 кг. Длина кривошипаOAl = 0,6 м, длина шатунаAB2ּl= 1,2 м. Угловая скорость кривошипа равна ω= 5 рад/с.

Определить модуль количества движения |Q| механизма в тот момент, когда уголα = π/2;

|Q| = … (кгּм/с).

+: 18

I: 211.

S: В кривошипно-шатунном механизмеОАВ, расположенном в горизонтальной плоскости, кривошипОАи шатунАВ имеют каждый массуm = 3 кг и длинуl = 0,6 м, а ползунВимеет массуm/2 = 1,5 кг. Угловая скорость кривошипа равна ω = 5 рад/с.

Определить модуль количества движения |Q| механизма в тот момент, когда уголα = 0;

|Q| = … (кгּм/с).

+: 9

I: 212.

S: Сплошной однородный диск радиусаR= 0,5 м и массыm = 6 кг жёстко скрепленный с прямолинейным стержнемАВ тоже массыmи длиной 2ּR, катится прямолинейно по гладкой поверхности так, что центрО имеет скоростьv₀= 5 м/с.

Определить модуль количества движения |Q| механизма;

|Q| = … (кгּм/с).

+: 60

I: 213.

S: Поезд массыm = 500 тонн после прекращения тяги тепловоза останавливается под действием силы тренияF_тр= 0,1 МН (мега-ньютон) через времяt= 1 мин. С какой скоростьюvшёл поезд до момента прекращения тяги тепловоза? v= …(м/с)

+: 12

I: 214.

S: Какова средняя сила давленияF на плечо при стрельбе из автомата, если масса пулиm = 10 г, а скорость пули при вылете из стволаv = 300 м/с? Число выстрелов из автомата в единицу времениn = 300 мин^{– 1}.F = … (Н).

+: 15

I: 215.

S: Орудие, имеющее массу стволаМ= 500 кг, стреляет в горизонтальном направлении. Масса снарядаm= 5 кг, его начальная скоростьv = 460 м/с. При выстреле ствол откатывается на расстояниеs= 40 см. Найти среднюю силу торможенияF(кН), возникающую в механизме, тормозящем ствол (результат вычисления округлить до целого числа);F = … (килоньютон)

+:13

I: 216.

S: Человек, стоящий на коньках на гладком льду реки, бросает камень массыm= 0,5 кг. Спустя времяt= 2 сек. камень достигает берега, пройдя расстояниеs = 20 м. С какой скоростьюuначинает скользить конькобежец, если его массаM = 60 кг? Трением пренебречь. (Результат вычисления округлить до второго знака после запятой включительно.)

u = … (м/с)

+: 0,08

I: 217.

S: Тело массыM = 990 г лежит на горизонтальной поверхности. В него попадает пуля массыm = 10 г и застревает в нём. Скорость пулиv = 700 м/с и направлена горизонтально. Какой путьsпройдет тело до остановки? Коэффициент трения между телом и поверхностьюk = 0,05. (Результат вычисления округлить до целого числа.) (g= 9,8 м/с²)s = … (м)

+:50

I: 218.

S: Ракета, имеющая вместе с зарядом массуM = 250 г, взлетает вертикально вверх и достигает высотыh = 150 м. Масса зарядаm = 50 г. Найти скоростьv истечения газов из ракеты (относительно земли), считая, что сгорание заряда происходит мгновенно. (Результат вычисления округлить до целого числа.)

v = … (м/с).

+:217

I: 219.

S: Масса платформы с орудием и боеприпасами составляетM = 20 тонн. С этой платформы, движущейся со скоростьюu= 9 км/час, производится выстрел из орудия. Снаряд массыm = 25 кг вылетает из ствола орудия со скоростьюv = 700 м/с (относительно орудия). Найти скорость платформыu₁ (км/час) непосредственно после выстрела, если направления движения платформы и выстрела совпадают. (Результат вычисления округлить до целого числа.)

u₁ = … (км/час).

+:6

I: 220.

S: Масса платформы с орудием и боеприпасами составляетM = 20 тонн. С этой платформы, движущейся со скоростьюu= 9 км/час, производится выстрел из орудия. Снаряд массыm = 25 кг вылетает из ствола орудия со скоростьюv = 700 м/с (относительно орудия). Найти скорость платформыu₁ (км/час) непосредственно после выстрела, если направления движения платформы и выстрела противоположны. (Результат вычисления округлить до целого числа.)

u₁ = … (км/час).

+: 12

I: 221.

S: Ядро, летевшее со скоростьюv = 200 м/с, разорвалось на два осколка с массамиm₁ = 10 кг иm₂ = 5 кг. Скорость первого осколкаv₁ = 300 м/с и направлена так же, как и скорость ядра до разрыва. Найти скоростьv₂ второго (меньшего) осколка;v₂ = … (м/с).

+:0

I: 222.

S: Центр масс колеса С движется по окружности радиусаR = 1,6 м согласно законуs= 4ּt (м). Масса колесаm = 15 кг.

Модуль главного вектора внешних сил, приложенных к колесу равен … (Н)

+:150

I: 223.

S: Трубка вращается вокруг вертикальной осиOz, её момент инерцииЈ_z= 0,075 кгּм². По трубке под действием внутренних сил системы движется шарикМ массойm= 0,1 кг. Когда шарик находится наОz, угловая скорость ω₀= 4 рад/с. Затем угловая скорость становится равной ω₁= 3 рад/с. Это стало на расстоянииl.

Определить расстояние l;l = … (м).

+:0,5

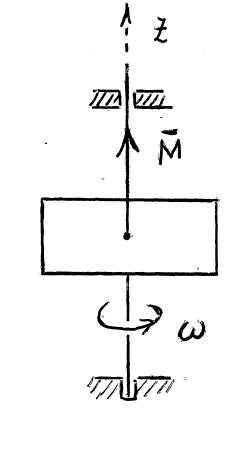
I: 224.

S: Тело вращается вокруг вертикальной осиOzпод действием пары сил с моментомМ = 16ּt (Нּм). Приt = 0 тело находилось в покое, а в моментt = 3 с угловая скоростьω= 2 рад/с.

Определить момент инерции (кгּм²) тела относительно осиOz.

Отметьте правильный ответ.

-: 24

+: 36

-: 42

-: 54

I: 225.

S: Горизонтальная трубкаCD может свободно вращаться вокруг вертикальной осиAB. Внутри трубки на расстоянииb = 0,2 м, от оси находится шарикM. В некоторый момент времени трубке сообщается начальная угловая скоростьω₀= 5 рад/сек. Определить угловую скоростьω трубки в момент, когда шарик вылетит из трубки. Момент инерции трубки относительно оси вращения равенJ = 0,7 кгּм², её длинаL = 1 м; шарик считать материальной точкой массыm = 0,5 кг; трением пренебречь.ω = … (рад/с).

+:3

I: 226.

S: Кривошипно-ползунный механизм прикреплён к станине массыM, установленной на гладком горизонтальном фундаменте. Масса ползунаBмеханизма равнаm, причёмM = 9ּm. Пренебрегая массой звеньевOA иAB, длины которых соответственноOA =l,OA иAB = 2ּl, найти максимальное значениеv_max скорости станины, если кривошип вращается с постоянной угловой скоростьюω и приt= 0 уголφ = 0 и начальная скорость станины равна нулю.

Искомая скорость v_max имеет видv_max=Κּωּl. ОпределитьΚ(результат вычисления – с точностью до первого знака после запятой).Κ = … .

+:0,1

I: 227.

S: Два вагона массm₁ = 20 тонн иm₂ = 30 тонн, двигавшиеся навстречу друг другу по горизонтальному прямолинейному участку пути со скоростямиv₁ = 3 м/с иv₂ = 2,5 м/с соответственно, сцепляются после соударения. Пренебрегая сопротивлениями движению, определить модуль скоростиv сцепа;v = … (м/с).

+:0,3

I: 228.

S: Через участки трубы постоянного сечения и различной формы со скоростьюv протекает жидкость заполняющая всё сечение трубы. Направление установившегося движения жидкости указано на рисунке стрелками. Полагая вес участков трубы и заполняющей их жидкости одинаковыми во всех четырёх случаях, установить, в каком из этих случаев сила нормального давления трубы на основание оказывается наибольшей

-: 1)

-: 2)

+: 3)

-: 4)

I: 229.

S: Диск массойm = 20 кг вращается равномерно вокруг неподвижной оси с угловой скоростьюω = 10 рад/с. Центр тяжести удалён от оси вращения на расстояние ОС = 0,5 см.

Модуль главного вектора внешних сил, приложенных к диску, равен … (Н).

+:10

I: 230.

S: Два груза одинаковой массыm = 2 кг каждый закреплены по концам невесомого нерастяжимого каната, переброшенного через однородный шкив массыm = 2 кг и радиусаr = 0,1 м. Зная угловую скорость вращенияω = 5 рад/с шкива и пренебрегая проскальзыванием каната относительно шкива, определить модуль количества движения |Q| данной механической системы; |Q| = … (кгּм/с).

+:0

I: 231.

S: Два груза одинаковой массыm = 2 кг каждый закреплены по концам невесомого нерастяжимого каната, переброшенного через однородный шкив массыm = 2 кг и радиусаr = 0,1 м. Зная угловую скорость вращенияω = 5 рад/с шкива и пренебрегая проскальзыванием каната относительно шкива, определить модуль кинетического момента |K_z| данной механической системы относительно оси вращения (числовой результат определить с точностью до второго знака после запятой);

|K_z| = … (кгּм²/с).

+:0,25

I: 232.

S: Снаряд массыm= 12 кг, летевший со скоростьюv = 800 м/с, разорвался в воздухе на 240 равных по массе осколков. Разлёт осколков в системе отсчёта, связанной с первоначальным снарядом, является сферически симметричным, и скорость каждого осколка в этой системе отсчёта равнаv_отн= 600 м/с. Модуль количества движения системы осколков относительно земли равен … (кгּм/с).

+: 9600

I: 233.

S: Шарик массойm= 100 г свободно упал на горизонтальную площадку, имея в момент удара скоростьv= 10 м/с. Найти модуль изменения количества движения при абсолютно неупругом |Q_{неупруг}| и абсолютно упругом |Q_упруг| ударах;

|Q_{неупруг}| = … (кгּм/с), |Q_упруг| = … (кгּм/с).

+: 1*2

I: 234.

S:Материальная точка массой 1 кг равномерно движется по окружности со скоростью 10 м/с. Найти модуль изменения количества движения за одну четверть периода |ΔQ_1/4|; половину периода |ΔQ_1/2|; целый период |ΔQ₁| (результат вычисления округлить до целого числа);

|ΔQ_1/4| = … (кгּм/с), |ΔQ_1/2| = … (кгּм/с), |ΔQ₁| = … (кгּм/с).

+: 14*20*0

I: 235.

S:Охотник стреляет из ружья с лодки по направлению её движения. Какую скоростьv имела лодка, если она остановилась после быстро следующих друг за другом выстрелов? Масса охотника с лодкой 200 кг, масса заряда 20 г. Скорость вылета дроби и пороховых газов 500 м/с. (Числовой результат определить с точностью до первого знака после запятой.)v= … (м/с).

+: 0,1

I: 236.

S:Вагон массой 20 т, движущийся со скоростью 0,3 м/с, нагоняет вагон массой 30 т, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после взаимодействия, если удар неупругий? (Числовой результат определить с точностью до второго знака после запятой.)

v= … (м/с).

+: 0,24

I: 237.

S:С лодки массой 200 кг, движущейся со скоростьюv=1 м/с, прыгает мальчик массой 50 кг в горизонтальном направлении с кормы в сторону, противоположную движению лодки, со скоростью 6 м/сотносительно лодки. Какова скоростьv₁ лодки после прыжка мальчика? (Числовой результат определить с точностью до первого знака после запятой.)v₁= … (м/с).

+: 2,5

I: 238.

S: С лодки массой 200 кг, движущейся со скоростьюv=1 м/с, прыгает мальчик массой 50 кг в горизонтальном направлении с носа лодки по ходу движения лодки со скоростью 6 м/сотносительно лодки. Какова скоростьv₁ лодки после прыжка мальчика? (Числовой результат определить с точностью до первого знака после запятой. Будьте внимательны со знаком значенияv₁!)v₁= … (м/с).

+: - 0,5

I: 239.

S:Мяч массой 100 г, летевший со скоростью 20 м/с, ударился о горизонтальную плоскость. Угол падения (угол между направлением скорости и перпендикуляром к плоскости) равен 60^о. Удар абсолютно упругий, а угол отражения равен углу падения. Модуль изменения количества движения равен … (кгּм/с).

+: 2

I: 240.

S:Какую скорость относительно ракетницы приобретает ракета массой 615 г, если газы массой 15 г вылетают из неё со скоростью 800 м/с?

Скорость ракеты равна … (м/с).

+: 20