Тема 2. Определение момента силы

40. Определить модуль (абсолютное значение) моментаМ_О

силы F = 50 (H) приα= 30⁰,a = 4 (м) и b = 2 (м) относительно

точки О(результат округлить до ближайшего целого числа);

| М_О | = … (Нм)

Ответ: 123 (Нм)

41. Определить модуль (абсолютное значение) моментаМ_А силыF = 150 (H) приα= 30⁰,a = 2 (м) и b = 5(м) относительно точкиА(результат округлить до ближайшего целого числа);| М_А | равен: … (Нм)

Ответ: 115 (Нм)

42. Определить модуль (абсолютное значение) моментаМ_В силыР = 120 (H)

при α= 30⁰,с = 3 (м) и d = 6 (м) относительно точкиB(результат округлить до ближайшего целого числа);| М_B | = … (Нм)

Ответ: 48 (Нм).

43. Определить модуль (абсолютное значение) моментаМ_О силыF = 350 (H)

α= 45⁰, приa = 7 (м) и b = 3 (м) относительно точкиО(результат округлить до ближайшего целого числа);| М_О | = … (Нм)

Ответ: 990 (Нм)

44. Определить модуль (абсолютное значение) моментаМ_А силыF = 420 (H) приα= 45⁰,a = 2 (м) и b = 6 (м) относительно точкиА(результат округлить до ближайшего целого числа);| М_А | = … (Нм)

Ответ: 1188 (Нм)

45. Определить модуль (абсолютное значение) моментаМ_В силыР = 320 (H)

α= 45⁰, прис = 4 (м) и d = 5 (м) относительно точкиB(результат округлить до ближайшего целого числа);| М_B | = … (Нм)

Ответ: 226 (Нм).

46. Определить модуль (абсолютное значение) моментаМ_О силыF = 120 (H) при

α= 60⁰,a = 4(м) и b = 2 (м) относительно точкиО(результат округлить до ближайшего целого числа);| М_О | = … (Нм)

Ответ: 92 (Нм)

47. Определить модуль (абсолютное значение) моментаМ_А силыF = 95 (H) приα= 60⁰,a = 6 (м) и b = 9(м) относительно точкиА(результат округлить до ближайшего целого числа);| М_А | = … (Нм)

Ответ: 455 (Нм)

48. Определить модуль (абсолютное значение) моментаМ_В силыР = 225 (H) при

α= 60⁰,с = 4 (м) и d = 7 (м) относительно точкиB(результат округлить до ближайшего целого числа);| М_B | = … (Нм)

Ответ: 914 (Нм).

49. Определить модуль (абсолютное значение) моментаМ_О силыF = 85 (H)

при α= 75⁰,a = 5 (м) и b = 3 (м) относительно точкиО(результат округлить до ближайшего целого числа);| М_О | = … (Нм)

Ответ: 136 (Нм)

50. Равнобокий прямоугольный уголок АВС (АВ=ВС=2м), весом которого пренебречь, находится в равновесии под действием силыF = 4H.

Найти: Модуль реактивного момента M_Aжесткой заделки А (результат округлить до ближайшего целого числа);M_A =. (Нм).

Ответ: M_A =11(Нм).

51.Равнобокий прямоугольный уголок АВС (АВ=ВС=2м), весом которого пренебречь, находится в равновесии под действием силыF = 4H.

Найти:

Модуль реактивного момента M_Aжесткой заделки А; M_A= … (Нм)

Ответ:M_A = 0.

52. Плоскость Р параллельна координатной плоскости Oxy. Сила F лежит в плоскости Р под углом α к прямой, параллельной оси Ox. Точка приложения силы A имеет координаты (a, b, c).

Укажите верное выражение момента силы F относительно оси Ox:

1. M_x (F) = - Fּsinαּb, 2) M_x (F) = Fּsinαּс, 3) M_x (F) = - Fּsinαּс,

4) M_x (F) = - Fּsinαּс + Fּcosαּa,, 5) M_x (F) = Fּsinαּb.

Ответ:2).

53. Плоскость Р параллельна координатной плоскости Oxz. Сила F лежит в плоскости Р под углом α к прямой, параллельной оси Ox. Точка приложения силы A имеет координаты (a, b, c).

Укажите верное выражение момента силы F относительно оси Oz:

1. M_z (F) = Fּcosαּb, 2) M_z (F) = - Fּcosαּb, 3) M_z (F) = - Fּcosαּa,

4) M_z (F) = Fּsinαּb, 5) M_z (F) = Fּcosαּa.

Ответ: 1)

54. Плоскость Р параллельна координатной плоскости Oyz. Сила F лежит в плоскости Р под углом α к прямой, параллельной оси Oy. Точка приложения силы A имеет координаты (a, b, c).

Укажите верное выражение момента силы F относительно оси Oz:

1. M_z (F) = Fּsinαּa, 2) M_z (F) = - Fּsinαּa, 3) M_z (F) = - Fּcosαּa,

4) M_z (F) = Fּcosαּb, 5) M_z (F) = -Fּcosαּb.

Ответ: 3)

55. Плоскость Р параллельна координатной плоскости Oxz. Сила F лежит в плоскости Р под углом α к прямой, параллельной оси Ox. Точка приложения силы A имеет координаты (a, b, c).

Укажите верное выражение момента силы F относительно оси Ox:

1. M_x (F) = Fּcosαּb, 2) M_x (F) = - Fּsinαּb, 3) M_x (F) = - Fּcosαּс,

4) M_x (F) = - Fּsinαּb + Fּcosαּc, 5) M_x (F) = Fּsinαּb.

Ответ: 2)

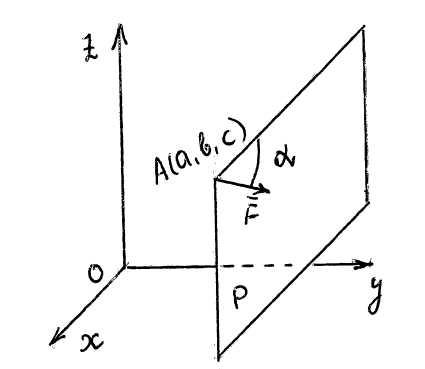
56. Плоскость Р параллельна координатной плоскости Oxy. Сила F лежит в плоскости Р под углом α к прямой, параллельной оси Ox. Точка приложения силы A имеет координаты (a, b, c).

Укажите верное выражение момента силы F относительно оси Oy:

1) M_y (F) = Fּsinαּa, 2) M_y (F) = - Fּsinαּa, 3) M_y (F) = Fּcosαּс,

4) M_y (F) = - Fּcosαּс, 5) M_y (F) = - Fּcosαּc -Fּsinαּa.

Ответ: 4)

57. Плоскость Р параллельна координатной плоскости Oyz. Сила F лежит в плоскости Р под углом α к прямой, параллельной оси Oy. Точка приложения силы A имеет координаты (a, b, c).

Укажите верное выражение момента силы F относительно оси Oy:

1. M_y (F) = Fּsinαּa, 2) M_y (F) = Fּsinαּb, 3) M_y (F) = - Fּsinαּa,

4) M_y (F) = - Fּsinαּb, 5) M_y (F) = - Fּcosαּc.

Ответ: 1)

58. Плоскость Р параллельна координатной плоскости Oxy. Сила F лежит в плоскости Р под углом α к прямой, параллельной оси Ox. Точка приложения силы A имеет координаты (a, b, c).

Укажите верное выражение момента силы F относительно оси Oz:

1. 

   M_z(F) = Fּcosαּb - Fּsinαּa, 2) M_z (F) = - Fּcosαּb,

2. M_z (F) = - Fּcosαּb + Fּsinαּa, 4) M_z (F) = Fּsinαּa,

5) M_z (F) = Fּcosαּb.

Ответ: 1)

59. Плоскость Р параллельна координатной плоскости Oyz. Сила F лежит в плоскости Р под углом α к прямой, параллельной оси Oy. Точка приложения силы A имеет координаты (a, b, c).

Укажите верное выражение момента силы F относительно оси Ox:

1) M_x (F) = Fּsinαּb, 2) M_x (F) = - Fּsinαּb, 3) M_x (F) = Fּcosαּb,

4) M_x (F) = Fּsinαּс - Fּcosαּb, 5) M_x (F) = Fּcosαּc - Fּsinαּb.

Ответ: 5)

60. Плоскость Р параллельна координатной плоскости Oxz. Сила F лежит в плоскости Р под углом α к прямой, параллельной оси Ox. Точка приложения силы A имеет координаты (a, b, c).

Укажите верное выражение момента силы F относительно оси Oy:

1. M_y (F) = Fּcosαּc, 2) M_y (F) = - Fּcosαּс + Fּsinαּa, 3) M_y (F) = - Fּsinαּa,

4) M_y (F) = - Fּsinαּa + Fּcosαּc, 5) M_y (F) = Fּsinαּa+ Fּcosαּc.

Ответ: 2)

61. Плоскость Р параллельна координатной плоскости Oxy. Сила F лежит в плоскости Р под углом α к прямой, параллельной оси Oy. Точка приложения силы A имеет координаты (a, b, c).

Укажите верное выражение момента силы F относительно осиOy:

1. M_y (F) = Fּsinαּa, 2) M_y (F) = Fּcosαּb, 3) M_y (F) = - Fּsinαּс,

4) M_y (F) = - Fּsinαּс + Fּcosαּa, 5) M_y (F) = - Fּcosαּc.

Ответ:3)

62. Определить модуль момента реакции М_В(R_A) шарнира А относительно точки В, если сила Р = 1000 Н, длина стержня АВ равна 3 метра. (Весом стержня пренебречь; результат округлить до ближайшего целого числа.) | М_В(R_A) | = … (Нּм).

Ответ: 866 (Нּм).

63. Определить модуль момента реакции М_С(R_В) шарнира В относительно точки С, если сила Р = 1000 Н, длина стержня ВС равна 2 метра. (Весом стержня пренебречь; результат округлить до ближайшего целого числа.) | М_В(R_A) | = … (Нּм).

Ответ: 707 (Нּм).

64. Определить момент реакции М_В(R_С) шарнира С относительно точки В, если сила Р = 800 Н приложена в точке D и направлена горизонтально, точки В и D расположены на одной вертикали и расстояние ВD = 3 метра. (Весом стержня пренебречь; результат округлить до ближайшего целого числа.) | М_В(R_С) | = … (Нּм).

Ответ: 2400 (Нּм).

65. Определить момент реакции М_С(R_D) шарнира D относительно точки С, если сила Р = 1000 Н, длина стержня СD равна 2 метра, α = 30^o. (Весом стержня пренебречь.) | М_C(R_D) | = … (Нּм).

Ответ: 1000 (Нּм).

66. Определить модуль момента реакции М_A(R_C) шарнира C относительно точки A, если сила Р = 800 Н, длина стержней: АВ = ВС, ВD = DС = 1 метр. (Весом стержня пренебречь.) | М_A(R_C) | = … (Нּм).

Ответ: 800 (Нּм).

67. Определить момент реакции М_B(R_C) шарнира C относительно точки B, если сила Р = 800 Н, момент пары М = 500 (Нм), длина стержня СВ = 1 метр. (Весом стержней пренебречь.) | М_В(R_C) | = … (Нּм).

Ответ: 0

68. Определить момент реакции М_D(R_В) шарнира B относительно точки D, если сила Р = 500 Н, момент пары М = 1000 (Нм), длина стержней СВ = ВА = 1 метр. (Весом стержней пренебречь.) | М_В(R_C) | = … (Нּм).

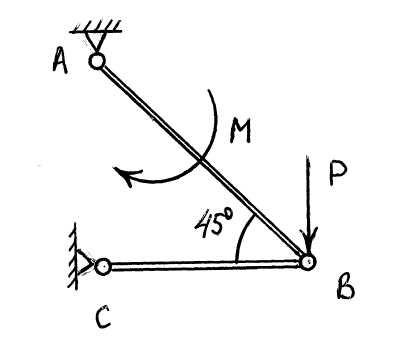
Ответ: 0

69. Определить момент реакции М_D(R_B) шарнира B относительно точки D, если сила Р = 800 Н приложена к середине стержня BD, ВD = 2 (м). (Весом стержня пренебречь.) | М_D(R_B) | = … (Нּм).

Ответ: 800 (Нм)

70. Определить момент реакции М_С(R_А) шарнира А относительно точки С, если сила Р = 900 Н, а = 1 (м), АС = 3 (м). (Весом стержней пренебречь.) | М_В(R_C) | = … (Нּм).

Ответ: 900 (Нм).

71. Равнобокий прямоугольный уголок АВС (АВ = ВС = 2 м), весом которого пренебречь, находится в равновесии под действием силыF = 440H.

Найти модуль момента М_С(X_A) горизонтальной составляющей реакцииX_Aжесткой заделки А относительно точки С (результат округлить до ближайшего целого числа);

| М_С(X_A)| = … (Нм)

Ответ:|М_С(X_A)| = 622 (Нм).

72.Равнобокий прямоугольный уголок АВС (АВ=ВС=2м), весом которого пренебречь, находится в равновесии под действием силыF = 800H.

Определить модуль момента М_С(Y_A) вертикальной составляющей реакцииY_Aжесткой заделки А относительно точки С (результат округлить до ближайшего целого числа);

| М_С(Y_A)| = … (Нм)

Ответ:|М_С(Y_A)| = 1131 (Нм).

73. Равнобокий прямоугольный уголок АВС (АВ = ВС = 2 м,AD=DB), весом которого пренебрегаем, находится в положении равновесия под действием силыF = 40 (Н) и равномерно распределенной нагрузки интенсивностьюq= 30 (Н/м).

Определить модуль реактивного момента жесткой заделки М_А; М_А = … (Нм).

Ответ: М_А = 20 (Н м).

74. Равнобокий прямоугольный уголок АВС (АВ = ВС = 2 м), весом которого пренебречь, находится в равновесии под действием силыF = 500 (H). Определить момент силы F относительно точки А (результат округлить до ближайшего целого числа);

М_А (F) = … (Нм).

Ответ: М_А (F)= 1414 (Н м).

75. Равнобокий прямоугольный уголок АВС (АВ=ВС=2м), весом которого пренебречь, находится в равновесии под действием силыF = 400H.

Определить алгебраический момент силы относительно точки В (результат округлить до ближайшего целого числа);М_В (F) = … (Нм).

Ответ: М_А (F)= - 566 (Н м).

76. 42.Равнобокий прямоугольный уголок АВС (АВ=ВС=2м), весом которого пренебрегаем, находится в положении равновесия под действием силыF = 500 (Н).

Определить реактивный момент М_А жесткой заделки А;М_А = … (Нм).

Ответ:.

77. Равнобокий прямоугольный уголок АВС (АВ=ВС=2м), весом которого пренебречь, находится в равновесии под действием силыF = 500 (H).

Определить алгебраический момент силы относительно точки В (результат округлить до ближайшего целого числа);М_В (F) = … (Нм).

Ответ: М_В (F ) = 707 (Нм).

78. 37.Равнобокий прямоугольный уголок АВС (АВ=ВС=2м), весом которого пренебрегаем, находится в положении равновесия под действием силыF = 450 (Н).

Определить момент вертикальной составляющей реакции в точке Y_A жесткой заделки А относительно точки С (результат округлить до ближайшего целого числа);

М_С (Y_A) = … (Нм).

Ответ: М_C (F ) = 636 (Нм).