
- •Федеральное агенство по образованию
- •1 Проектирование монолитного ребристого перекрытия
- •1.2 Расчет и конструирование второстепенной балки
- •Расчет и конструирование сборной предварительно-
- •Напряженной ребристой плиты перекрытия
- •Расчетный пролет и нагрузки
- •Номинальную ширину плиты примем равной 1600 мм.
- •Расчет и конструирование ригеля
- •Эпюра изгибающих моментов
- •Эпюра арматуры и поперечной силы
- •4 Расчет и конструирование средней колонны
- •5 Расчет и конструирование фундамента
- •Используемая литература
- •Часть 1,Часть 2,Часть 3,Часть 4.-н.Челны., 2001.
Расчет и конструирование сборной предварительно-
Напряженной ребристой плиты перекрытия
Расчетный пролет и нагрузки
Номинальную ширину плиты примем равной 1600 мм.
Подсчет нагрузок.
|
Вид нагрузки |
Нормативная Н/м2 |
Коэфф-т надежности по нагрузке |
Расчетная Н/м2 |
|
ПОСТОЯННАЯ 1. Собств. вес плиты с овальными пустотами 2. То же слоя цем. стяжки =20 мм (=2200 кг/м2) 3. То же керамических плиток =13 мм (=1800 кг/м2) |
2500
440
240 |
1.1
1.3
1.1 |
2750
572
264 |
|
Итого:
ВРЕМЕННАЯ В том числе: Длительная Кратковременная
ПОЛНАЯ В том числе: Постоянная и длительная
|
3180
4600
3220 1400
7780
6400
|
-
1,2
1,2 1,2
-
-
|
3586
5520
3864 1656
9106
-
|
Расчетная нагрузка на 1м длины при ширине плиты 1,6 м с учетом коэффициента надежности по назначению здания n=0.95.
а) Постоянная g=3,586*1,6 *0.95=5,45кН/м
б) Полная (g+)=9,106*1,6*0.95=13,84кН/м
в) Временная =5,52*1,6*0.95=8,39 кН/м
Нормативная нагрузка на 1м длины.
а) Постоянная gн=3,18*1,6*0.95=4,83кН/м
б) Полная (gн+н)=7,78*1,6*0.95=11,83кН/м
в) В том числе постоянная и длительная 6,4*1,6*0.95=9,73кН/м
г) Кратковременная: 1,4*1,6*0.95=2,13кН/м
Для
определения расчетного пролета панели
l0
предварительно
назначим сечение ригеля
![]() ,
,![]() ;принимаем
;принимаем![]()
![]()
При
опирании панели на полки ригеля расчетный
пролет
![]()
 Усилия:
а) От расчетных
нагрузок:
Усилия:
а) От расчетных
нагрузок:
![]() ;
;
![]()
б) От нормативной полной:
![]() ;
;
в) От нормативной постоянной и длительной :
![]() ;
;
г) От нормативной кратковременной:
![]() ;
;
Установление поперечных размеров сечения панели
а) Высота сечения ребристой предварительно-напряженной панели:
![]() принимаем h=25
см
принимаем h=25
см
б)
Рабочая высота сечения
![]()
в) Ширина продольных ребер понизу 7 см.
г) Ширина верхней полки 156см.
Расчетная ширина ребра b=2*7=14см.
Сечение и расчетное сечение панели.
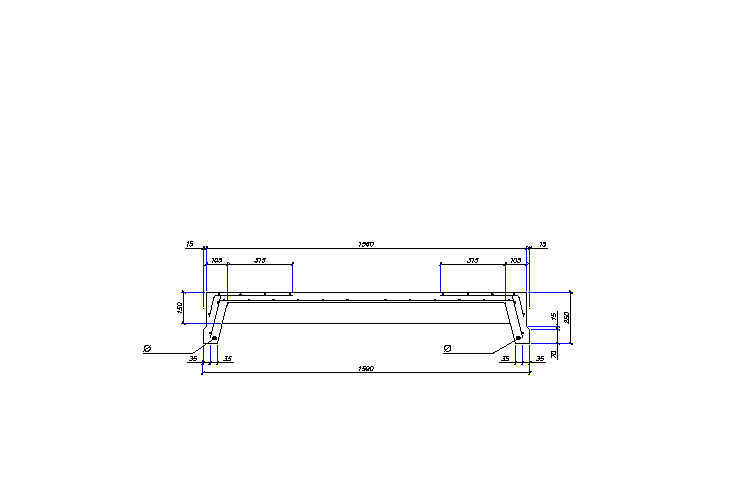
 Характеристики
прочности бетона и арматуры
Характеристики
прочности бетона и арматуры
Ребристую предварительно-напряженную панель армируют стержневой арматурой класса А-600 с механическим натяжением на упоры форм. К трещиностойкости плиты предъявляют требования 3-й категории.
Бетон тяжелый, класса B-20.
|
Характеристики |
Нормативное значение |
Расчетное значение |
|
Призменная прочность Растяжение осевое |
Rbn=Rb,ser=14,5 МПа Rbtn=Rbt,ser=1,4 МПа |
Rb=11,5 МПа Rbt=0,9 МПа |
Коэффициент условий работы b2=0.9.
Начальный модуль упругости Eb=24*103МПа
Передаточная прочность бетона Rb устанавливается так, чтобы при обжатии отношение напряжений bp/Rbp0.75
Арматура продольных ребер – А-600.
Нормативное сопротивление Rsn=590 МПа.
Расчетное сопротивление Rs=510 МПа.
Модуль упругости Es=190000 МПа.
Предварительное напряжение арматуры принимают равным:
![]()
Проверяют выполнение условия: при механическом способе натяжения:
![]() ;
;
![]() -
условие выполняется.
-
условие выполняется.
Определяем предельное отклонение предварительного напряжения:
![]() .
.
При проверке по образованию трещин в верхней зоне плиты при обжатии принимают sp=1+0.1=1,1
Коэффициент точности натяжения: sp=1-0.1=0,9.
Предварительное
напряжение с учетом точности натяжения:
![]()
Расчет прочности по сечению, нормальному к предельной оси
М=55,7 кН*м. Сечение тавровое с полкой в сжатой зоне.
Вычисляем
![]()
=0,071;
![]() -нейтральная
ось проходит в пределах сжатой полки,
=0,964
-нейтральная
ось проходит в пределах сжатой полки,
=0,964
Характеристика сжатой зоны
![]()
Граничная высота сжатой зоны
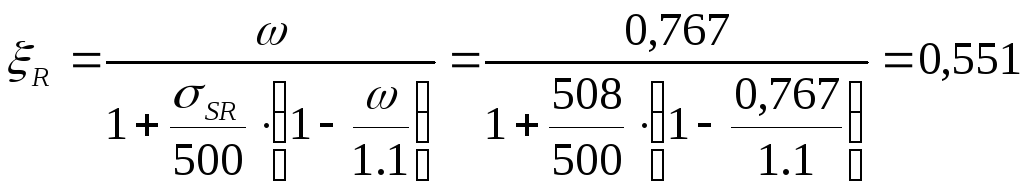 ;
;
где
![]() ;
;
В знаменателе 500МПа, поскольку b2<1.
Коэффициент условий работы, учитывающий сопротивление напрягаемой
арматуры выше условного предела текучести:
![]() ;
;
=1,15 - для арматуры класса A-600. Принимаем S6=1,15.
Вычисляем площадь сечения растянутой арматуры:
![]()
Принимаем 216 A-600 с AS=4,02см2.
Расчет прочности панели по сечению, наклонному к продольной оси
Qmax=39,3кН
Влияние продольного усилия обжатия:
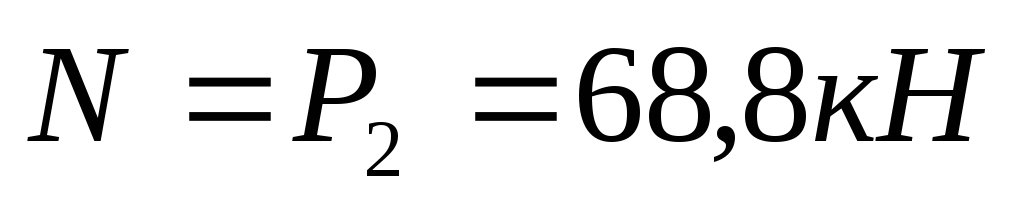 ;
;
![]()
принимаем
![]() .
.
Проверяем требуется ли поперечная арматура по расчету:
![]()
![]() -
удовлетворяется.
-
удовлетворяется.
При
![]()
![]() -
это расстояние от вершины наклонного
сечения до опоры.
-
это расстояние от вершины наклонного
сечения до опоры.
Проверяем второе условие:
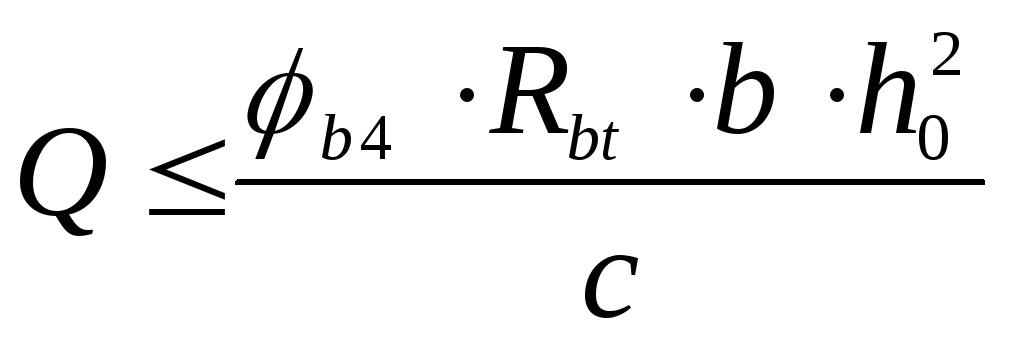 ,
,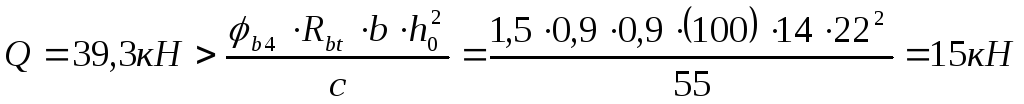 условие не выполняется, значит,
требуется расчет поперечной арматуры.
условие не выполняется, значит,
требуется расчет поперечной арматуры.На приопорных участках длиной l/4 устанавливаем в каждом ребре между пустотами стержни 5В500 с шагом
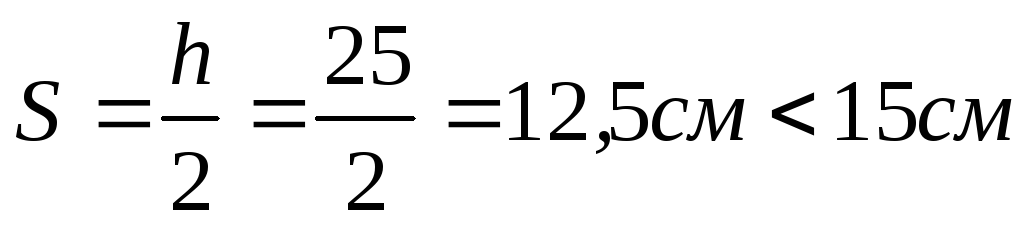 .
.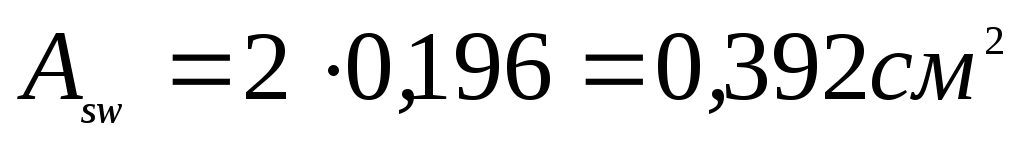 ;
;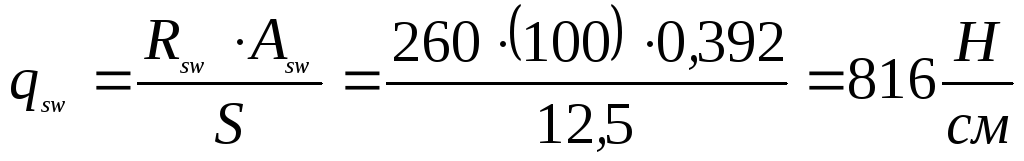
Влияние свесов сжатых полок (при 2 ребрах):
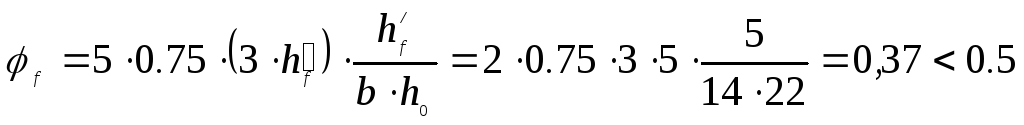
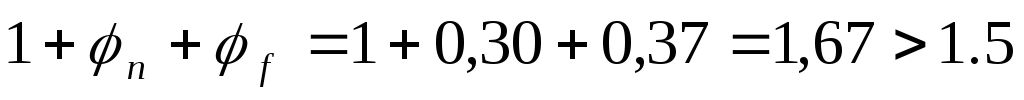 ,
принимаем 1.5
,
принимаем 1.5
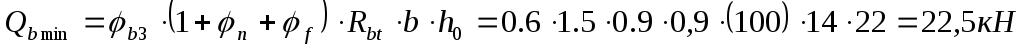
 Условие
Условие
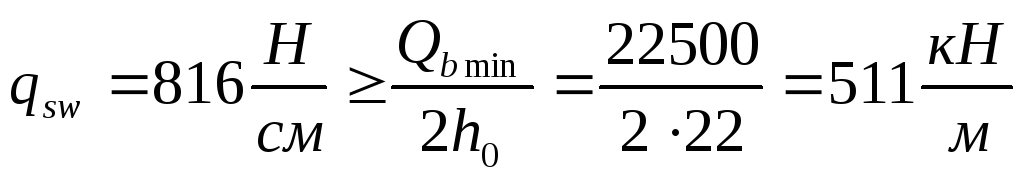 удовлетворяется
удовлетворяетсяТребование
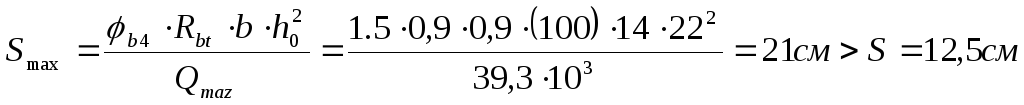 удовлетворяется
удовлетворяется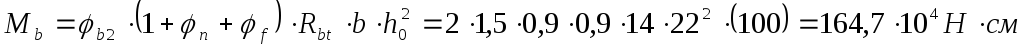
 ,
то вычисляем
,
то вычисляем
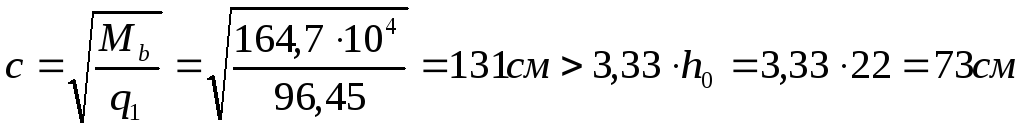 ,
,
принимаем с=73см
Тогда
 , принимаем
, принимаем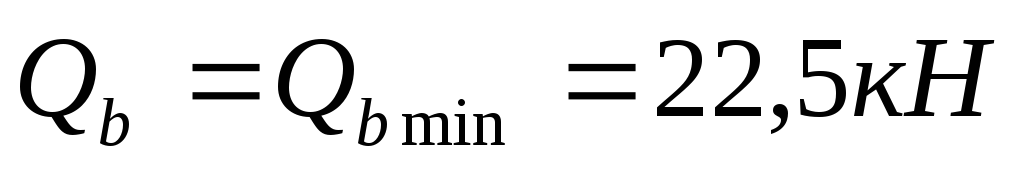
Поперечная сила в вершине наклонного сечения:
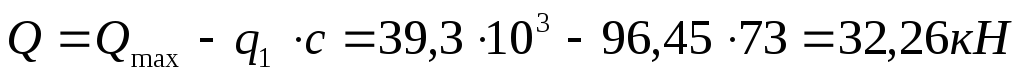
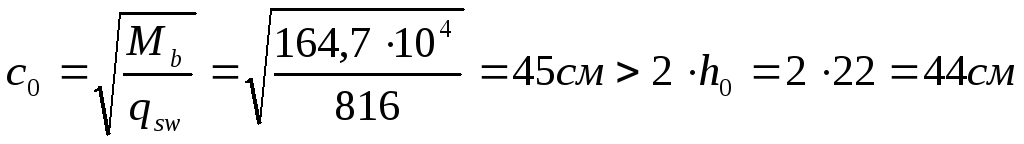 ,
принимаем
,
принимаем
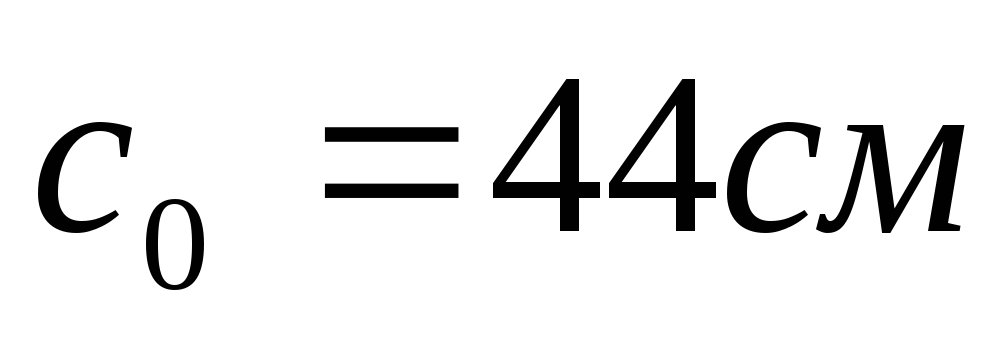
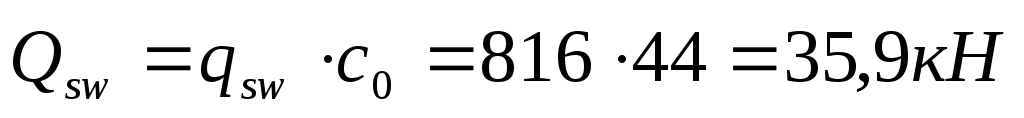
Проверяем условие прочности:
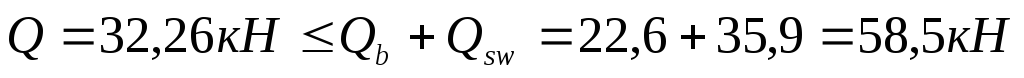
условие прочности обеспечено
Проверим прочность по сжатой наклонной полосе:
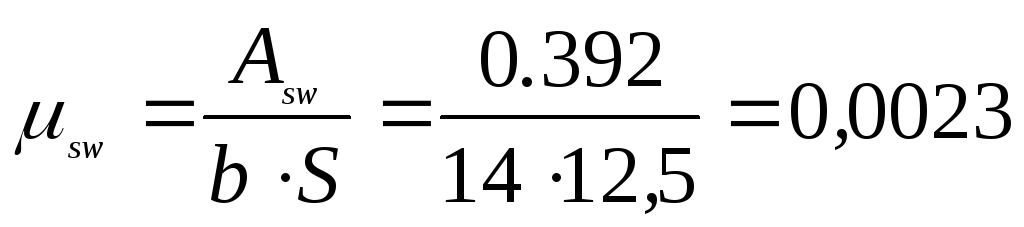 ;
;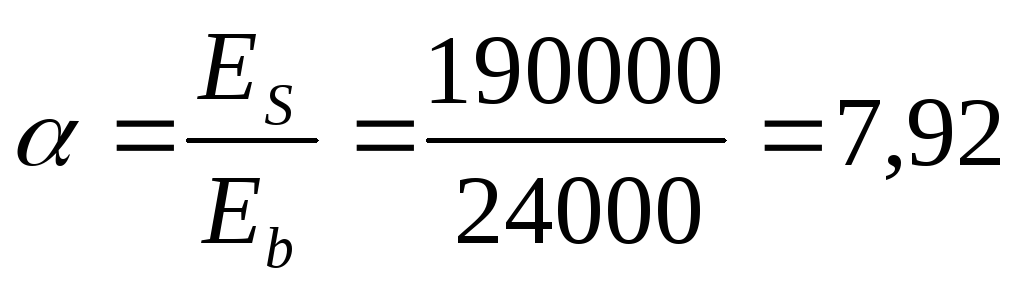 ;
;
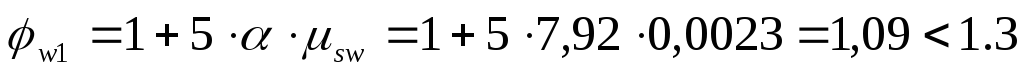
=0.01 - для
тяжелого бетона;
![]()
Условие прочности:
![]()
удовлетворяется.
Хомуты объединены в один каркас К-1 (по одному в каждом ребре), в котором верхняя ненапрягаемая арматура принимается из расчета на монтажные нагрузки. В данном случае продольные стержни приняты конструктивно соответственно 18A400 с AS=0.503см2 и 16A400 с AS=0.283см2.
Определение геометрических характеристик приведенного сечения.
Отношение модулей упругости:
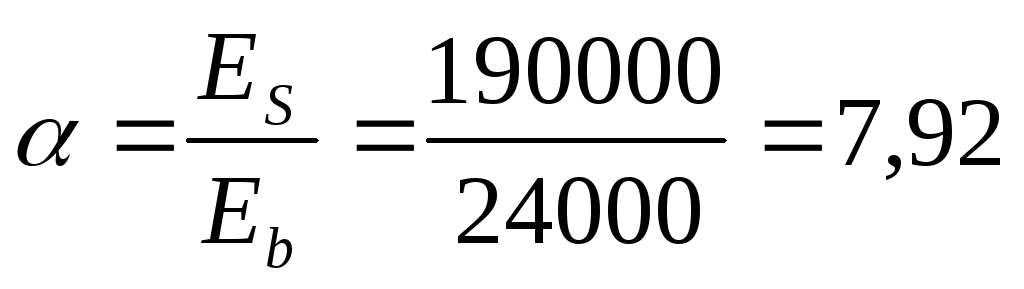
Площадь приведенного сечения:

Статический момент относительно нижней грани сечения панели:
![]()
 Расстояние
от нижней грани до центра тяжести
приведенного сечения:
Расстояние
от нижней грани до центра тяжести
приведенного сечения:
![]()
Момент инерции:
![]()
Момент сопротивления приведенного сечения по нижней зоне:
![]()
Момент сопротивления приведенного сечения по верхней зоне:
![]()
Расстояние от ядровой точки, наиболее удаленной от растянутой (верхней зоны) до центра тяжести приведенного сечения:
![]()
То же, наименее удаленной от растянутой зоны (нижней):
![]() ;
где
;
где
![]()
Упругопластический момент сопротивления по растянутой зоне:
![]()
=1.75-для таврового сечения с полкой в сжатой зоне.
Упругопластический момент сопротивления по растянутой зоне в стадии изготовления и обжатия элемента:
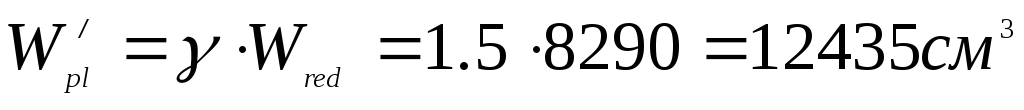
=1.5-для таврового
сечения с полкой в растянутой зоне при
![]() и
и![]()
Определение потерь предварительного напряжения
Коэффициент
точности натяжения арматуры
![]() .
.
Потери от релаксации напряжений в арматуре при механическом способе
натяжения:
![]()
Потери от температурного перепада между натянутой арматурой и упорами 2=0
Потери от деформации анкеров, расположенных у натяжных устройств:
![]()
где
![]()
![]() длина
натягиваемого стержня(расстояние между
наружными гранями формыили стенда)
длина
натягиваемого стержня(расстояние между
наружными гранями формыили стенда)
Усилие обжатия:
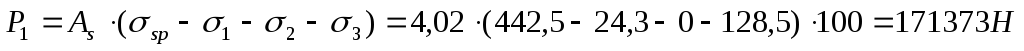
Эксцентриситет этого усилия относительно центра тяжести приведенного сечения:
![]()
Напряжение в бетоне при обжатии:
![]()
 Передаточная
прочность бетона устанавливается из
условия:
Передаточная
прочность бетона устанавливается из
условия: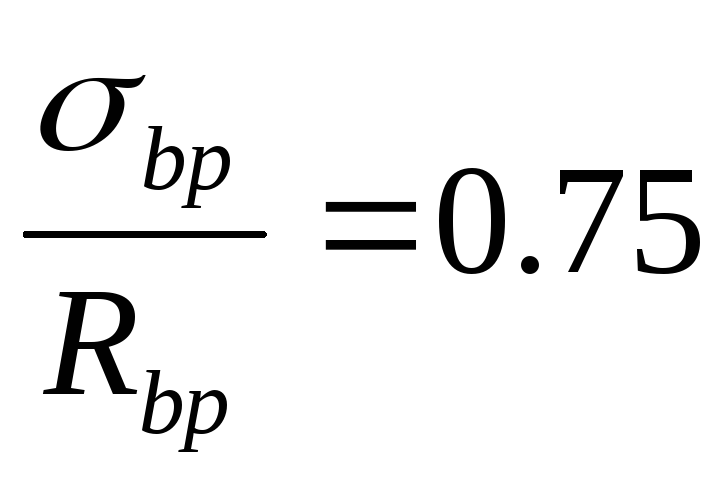 ;
;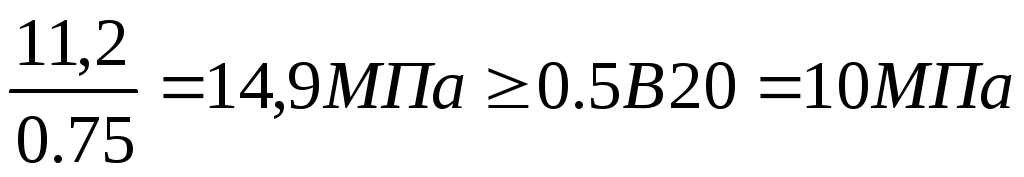 .
ПринимаемRbp=11
МПа.
.
ПринимаемRbp=11
МПа.Сжимающее напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от усилия обжатия P1 и c учетом изгибающего момента от веса плиты:
![]()
Тогда:
![]()
Потери от быстронатекающей ползучести при:
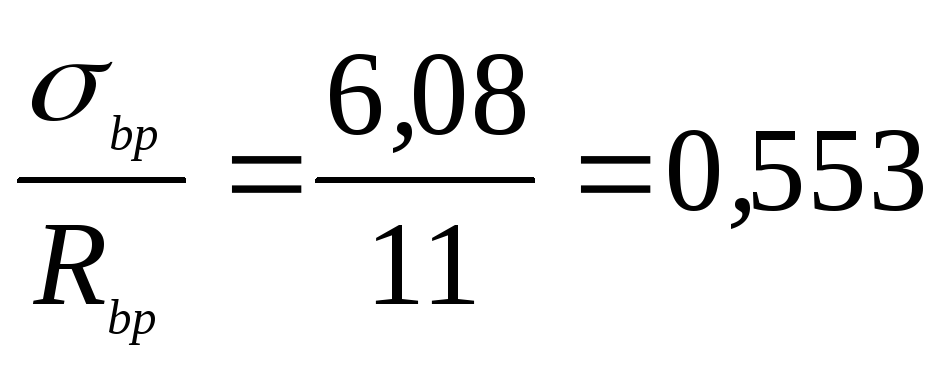 и при <0.8
и при <0.8
![]()
составляют:
![]()
Первые потери:
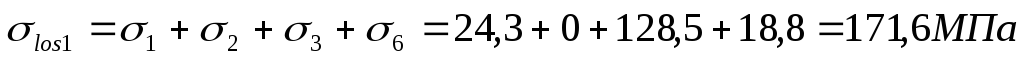
С учетом потерь los1:
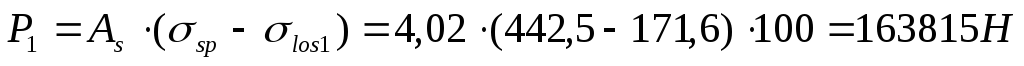
![]()
Потери от усадки бетона:
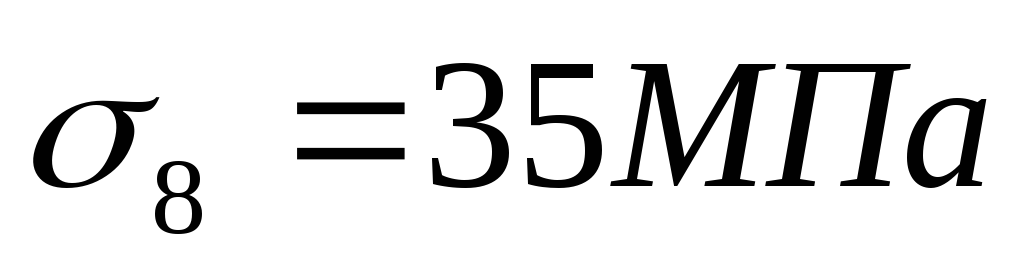
Потери от ползучести бетона при
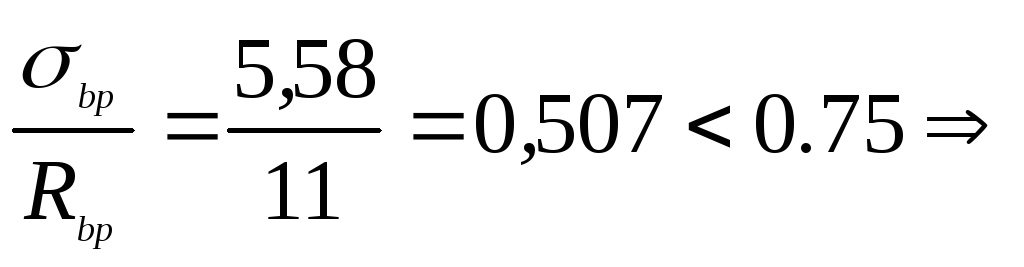 составляем
составляем
![]()
Вторые потери:
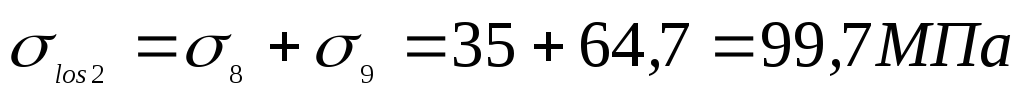
Полные потери:
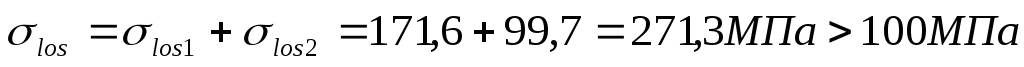 ,
что >установленногоmin
(то есть условие выполняется). Принимаем
,
что >установленногоmin
(то есть условие выполняется). Принимаем
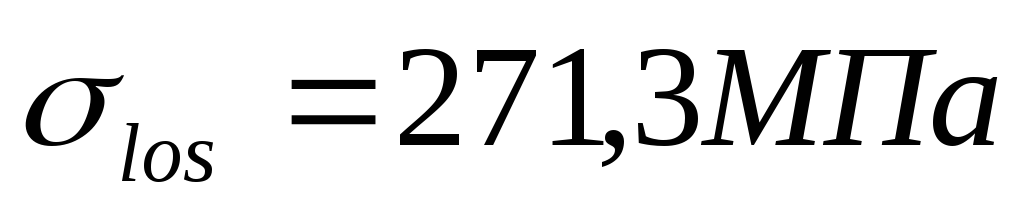 .
.Усилие обжатия с учетом полных потерь:
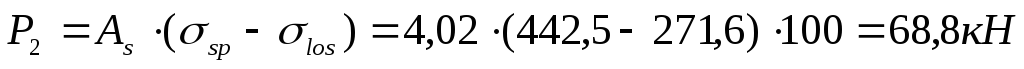 .
.
Расчет по образованию трещин, нормальных к продольной оси
f=1 – коэффициент надежности по нагрузке.
Mн=47,6 кНм.
Проверим выполнение
условия
![]()
Вычислим момент образования трещин по приближенному способу ядровых моментов:
![]()
![]()
 Поскольку
Поскольку
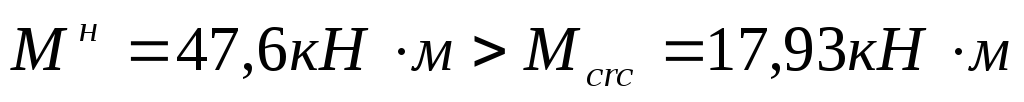 ,
то трещины в растянутой зоне образуются,
т.е. необходим расчет по раскрытию
трещин.
,
то трещины в растянутой зоне образуются,
т.е. необходим расчет по раскрытию
трещин.Проверим образуются ли начальные трещины в верхней зоне плиты при ее обжатии при значении коэффициента точности натяжения sp=1,1. Изгибающий момент от веса плиты M=16,1кНм.
Расчетное условие:
![]() ;
;![]() -
условие выполняется, значит, начальные
трещины не образуются.
-
условие выполняется, значит, начальные
трещины не образуются.
Расчет по раскрытию трещин нормальных к
продольной оси при sp=1
Предельная ширина раскрытия трещин:
непродолжительная acrc=0.3мм
продолжительная acrc=0.2мм
2. Изгибающие моменты от нормативных нагрузок:
постоянной и длительной Mн=47,6кНм;
суммарной Mн=55,7кНм
3. Приращение напряжений в растянутой арматуре от действия постоянной и длительной
нагрузок:![]()
где
![]() -плечо
внутренней пары сил.
-плечо
внутренней пары сил.
esp=0, так как усилие обжатия P приложено в ц.т. площади площади нижней напрягаемой арматуры.
![]() -
момент сопротивления по растянутой
арматуре.
-
момент сопротивления по растянутой
арматуре.
Приращение напряжений в арматуре от действия полной нагрузки:
![]()
Ширина раскрытия трещин от непродолжительного действия всей нагрузки:


![]() -
диаметр продольной арматуры.
-
диаметр продольной арматуры.
Ширина раскрытия трещин от непродолжительного действия постоянной и длительной нагрузки:
![]()
Ширина раскрытия трещин от постоянной и длительной нагрузок:
![]() ;
где l=1.5
;
где l=1.5
Непродолжительная ширина раскрытия трещин:
![]()
Продолжительная ширина раскрытия трещин:
![]()
