
2014-15_NULEVOJ_TEST_Vvedenie_v_analiz_Proizv
.doc
НУЛЕВОЙ ВАРИАНТ ТЕСТОВ:
Разделы: «Введение в анализ»; «Дифференциальное исчисление ФОП и ФНП».
|
Раздел: ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ. |
||||
|
Тема
5.1: Функция-1. Область определения,
чётность (нечётность) функции одной
переменной. Элементы поведения основных
элементарных функций (чётность и
нечётность, периодичность, монотонность,
ограниченность):
|
||||
|
1. |
Областью
определения функции
1)
|
4) |
||
|
2. |
Даны функции А: 1) только А 2) только В 3) А и В 4) ни А, ни В |
4) |
||
|
3. |
Какие из утверждений для
функции
1) периодическая 2) немонотонная 3) неограниченная 4) нечётная
В ответе указать все верные утверждения. |
1)2)4) |
||
|
4 |
Выяснить является ли функция
1) четная 2) нечетная 3) ни четная, ни нечетная |
1) |
||
|
5 |
Выяснить является ли функция
1) четная 2) нечетная 3) ни четная, ни нечетная |
2) |
||
|
Тема 5.2: Функция-2. Область определения, множество значений, чётность (нечётность) функции одной переменной. Свойства чётных и нечётных функций. |
||||
|
1. |
Областью
определения функции
|
|
||
|
2. |
Функция
1)
|
2) |
||
|
Тема
5.3: Пределы-1. Пределы рациональных
выражений
|
||||
|
1. |
Предел
1)
|
4) |
||
|
2. |
Если
|
|
||
|
3. |
Предел
1)
|
4) |
||
|
4. |
Предел
Ответ
записать в виде:
|
|
||
|
5 |
Предел
Запишите ответ. |
1 |
||
|
Тема 5.4: Пределы-2. Пределы иррациональных выражений. Пределы степенно-показательных функций. Пределы тригонометрических выражений, с использованием первого замечательного предела и его следствий. |
||||
|
1. |
Предел
1)
|
5) |
||
|
2. |
Предел
Ответ
записать в виде:
|
4 |
||
|
3. |
Предел
Ответ
записать в виде:
|
3 |
||
|
4. |
Предел
Ответ
записать в виде:
|
2 |
||
|
Тема 5.5: Пределы-3. Пределы иррациональных выражений. Пределы степенно-показательных функций. Пределы тригонометрических выражений, с использованием первого замечательного предела и его следствий. Пределы выражений, содержащих факториал. |
||||
|
1. |
Предел
Ответ
записать в виде:
|
12 |
||
|
2. |
Предел
|
3 |
||
|
3. |
Предел
1)
|
2) |
||
|
4 |
Предел
Ответ
записать в виде:
|
4 |
||
|
5 |
Предел
Ответ
записать в виде:
|
|
||
|
6 |
Предел Ответ
записать в виде:
|
3 |
||
|
Тема 5.6: Непрерывность. Непрерывность функции в точке. Точки разрыва функции, их классификация. Непрерывность функции, задаваемой несколькими аналитическими выражениями. |
||||
|
1 |
Даны функции
A:
Непрерывными из них в точке
1) только А 2) только В 3) А и В 4) ни А, ни В |
3) |
||
|
2 |
Дана функция
1)
В ответе указать все точки разрыва функции. |
2)3)4) |
||
|
3. |
Функция
|
17 |
||
|
4. |
Точка
1)
В
ответе указать все функции, для которых
|
1)2)4) |
||
|
5 |
Даны функции А:
A:
Непрерывными из них в точке
1) только А; 2) только В; 3) А и В; 4) ни А, ни В. |
2) |
||
|
6. |
Точка
1)
3) В
ответе указать все функции, для которых
|
1), 2), 4) |
||
|
7 |
Точка
1)
3) В
ответе указать все функции, для которых
|
1), 4) |
||
|
8 |
Точка
1)
3) В
ответе указать все функции, для которых
|
2) |
||
|
Тема 5.7: Введение в анализ (теория). Теоретические вопросы (в объёме вопросов к экзамену), в том числе: бесконечно малые и большие функции, их свойства; свойства функций, имеющих конечный предел; сходимость ограниченных и монотонных числовых последовательностей; неопределённые выражения; определение непрерывности функции в точке; определение точек разрыва функции и их классификация; свойства функций непрерывных на отрезке (об ограниченности функции, принятии ею наибольших и наименьших значений). Условие существования вертикальной асимптоты. Взаимосвязь монотонности и ограниченности последовательности с существованием её предела. Взаимосвязь функции, имеющей предел с бесконечно малой функцией. |
||||
|
Раздел: ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ. |
||||
|
Тема
6.1: Производная-1. Производная
|
||||
|
1 |
Производная
1)
|
2) |
||
|
2. |
Соответствие
функций
1:
2:
3:
|
1-1 2-2 3-3 |
||
|
3. |
Если
Ответ записать в виде:
|
11 |
||
|
4. |
Если
|
-7 |
||
|
5. |
Если
|
-8 |
||
|
6 |
Если
|
1 |
||
|
Тема 6.2:
Производная-2. Производная
|
||||
|
1. |
Если
1)
|
2) |
||
|
2. |
Если функции
|
1 |
||
|
3 |
Если
|
241 |
||
|
4 |
Если
|
66 |
||
|
5 |
Соответствие функций
1:
1: В ответе указать пары соответствующих друг другу функций и их вторых производных. |
1-1 2-2 3-3 |
||
|
Тема 6.3: Производная-3. Неявная производная; производная степенно-показательной функции; касательная и нормаль неявной и параметрической кривой. |
||||
|
1 |
Если
1)
3)
5)
|
1) |
||
|
2 |
Если функция
Ответ записать в виде:
|
-5 |
||
|
3 |
Уравнение касательной к
графику функции
|
-16,8 |
||
|
4 |
Уравнение нормали к графику
функции, заданной неявно уравнением
|
14,13 |
||
|
Тема 6.4: Приложения производной-1. Касательная и нормаль. Интервалы монотонности. Наибольшее и наименьшее значения функции на отрезке. Точки локального экстремума. Правило Лопиталя. |
||||
|
1. |
Если
Ответ записать в виде:
|
0,3 |
||
|
2. |
Предел
Ответ записать в виде:
|
18 |
||
|
3. |
Уравнение нормали к графику функции
1) |
3) |
||
|
4. |
Если
1)
|
3) |
||
|
5. |
Если
Ответ записать в виде:
|
1 |
||
|
6 |
Функция
Ответ введите в виде:
|
0,5 |
||
|
7 |
Функция
Ответ введите в виде:
|
0,2 |
||
|
8 |
Уравнение касательной к графику
функции
Ответ введите в виде:
|
-4,6 |
||
|
9 |
По правилу Лопиталя предел
|
|
||
|
10 |
По правилу Лопиталя предел
|
1 |
||
|
Тема 6.5: Приложения производной-2. Наклонные асимптоты. Точки перегиба. Интервалы выпуклости и вогнутости. Уравнения касательной и нормали (с вводом ответа). Правило Лопиталя (с вводом ответа). |
||||
|
1 |
Наклонной асимптотой
графика функции
Ответ записать в виде:
|
4,0 |
||
|
2 |
Если
Ответ записать в виде:
|
0,4 |
||
|
3 |
Интервалом вогнутости функции
|
-1,1 |
||
|
4 |
По правилу
Лопиталя предел
Ответ записать в виде: a, b |
2,2 |
||
|
Тема 6.7: Производная (теория-1). Теоретические вопросы (в объёме вопросов к экзамену), в том числе: определение производной, её геометрический смысл; условия возрастания и убывания дифференцируемой функции; условия выпуклости и вогнутости дифференцируемой функции; стационарная и критическая точки функции; необходимое и достаточное условия существования локального максимума и минимума функции (через первую и вторую производные); условия существования точек перегиба графика функции; правило Лопиталя (к раскрытию каких неопределённостей непосредственно применимо). |
||||
|
Тема 6.8: Производная (теория-2). Теоретические вопросы (в объёме вопросов к экзамену), в том числе: определение производной, её геометрический смысл; условия возрастания и убывания дифференцируемой функции; условия выпуклости и вогнутости дифференцируемой функции; стационарная и критическая точки функции; необходимое и достаточное условия существования локального максимума и минимума функции (через первую и вторую производные); условия существования точек перегиба графика функции; правило Лопиталя (к раскрытию каких неопределённостей непосредственно применимо). Взаимосвязь понятий (ограниченность, непрерывность, дифференцируемость). Теоремы Ролля, Лагранжа, Коши, их применение. |
||||
|
1 |
Функция
|
5 |
||
|
Тема 7.1: Производная ФНП-1. Первая частная производная. Первый дифференциал. |
||||
|
1. |
Частная производная
1)
|
5) |
||
|
2. |
Полный дифференциал функции
|
3/32,3/64 |
||
|
3. |
Если
1)
|
2) |
||
|
Тема 7.2: Производная ФНП-2. Первый дифференциал. Первая и вторая частные производные. |
||||
|
1 |
Для функции
1)
|
4) |
||
|
2 |
Если
|
4 |
||
|
3 |
Если
|
2 |
||
|
Тема 7.3: Производная ФНП-3. Производная по направлению. Полный дифференциал. |
||||
|
1. |
Если
1)
|
2) |
||
|
2 |
Полный дифференциал функции
|
-1,-4 |
||
|
3 |
Производная
|
|
||
|
4 |
Полный дифференциал функции
|
-60,-17 |
||
|
Тема 7.4: Приложения
производной ФНП-1. Локальный
экстремум функции
|
||||
|
1 |
Функция
|
53/4 |
||
|
2 |
Функция
|
-5,-1,1 |
||
|
3 |
Если
|
|
||
|
4 |
Модуль градиента
|
|
||
|
Тема 7.5: Приложения
производной ФНП-2. Градиент и
его модуль. Касательная плоскость
для поверхности заданной явно и неявно.
Локальный экстремум функции
|
||||
|
1. |
Градиентом функции
1) |
4) |
||
|
2. |
Модуль градиента
|
89 |
||
|
3. |
Уравнение касательной
плоскости к поверхности
|
|
||
|
4. |
Уравнение касательной
плоскости к поверхности заданной
неявным уравнением
|
|
||
|
Тема 7.6: ФНП
(теория-1).Теоретические вопросы
(в объёме вопросов к экзамену), в
том числе: область определения; формула
для дифференциала первого и второго
порядков, формула для приближённых
вычислений с помощью первого
дифференциала; определение стационарной
точки; необходимое и достаточное
условия существования локального
максимума и минимума функции
|
||||
|
1. |
Областью определения функции
1)
|
2) |
||
|
Тема 7.7: ФНП
(теория-2).Теоретические вопросы
(в объёме вопросов к экзамену), в
том числе: область определения; формула
для дифференциала первого и второго
порядков, формула для приближённых
вычислений с помощью первого
дифференциала; определение стационарной
точки; необходимое и достаточное
условия существования локального
максимума и минимума функции
|
||||

 является множество:
является множество: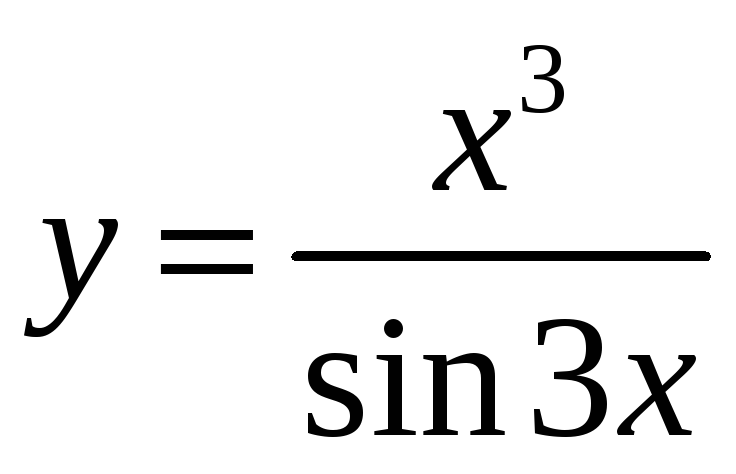 .
Нечётными из них (в
области их определения) являются:
.
Нечётными из них (в
области их определения) являются: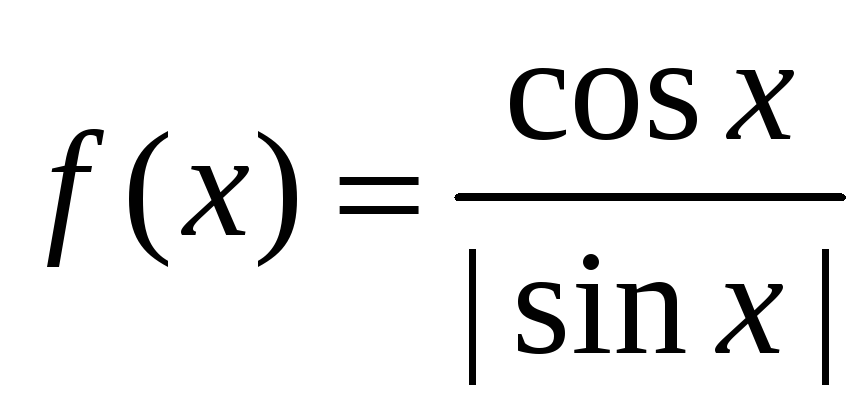 четной или нечетной (указать номер
правильного ответа):
четной или нечетной (указать номер
правильного ответа):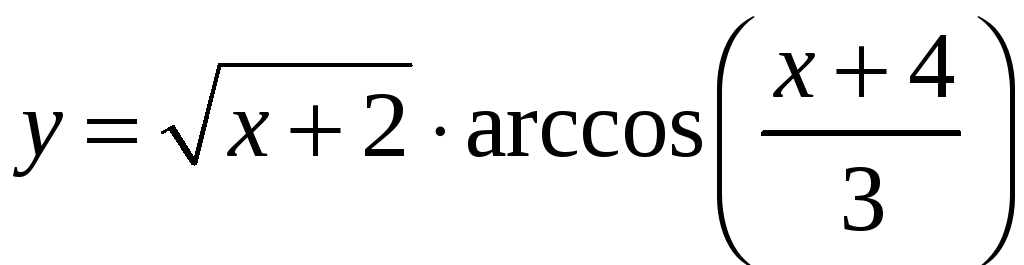 является отрезок
является отрезок
 ,
,
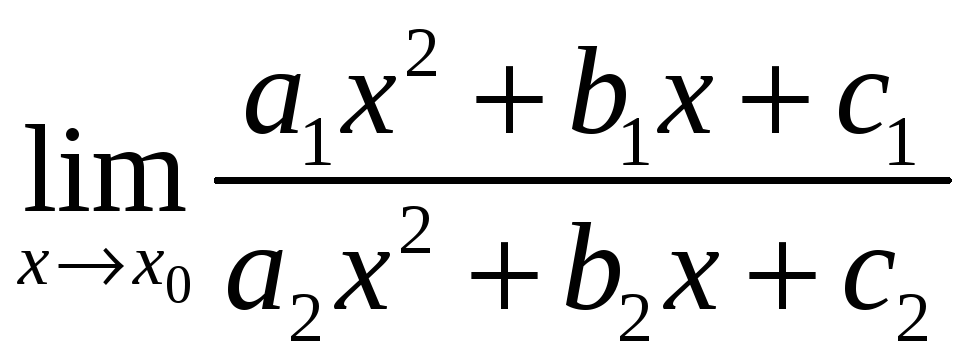 .
.
 равен:
равен: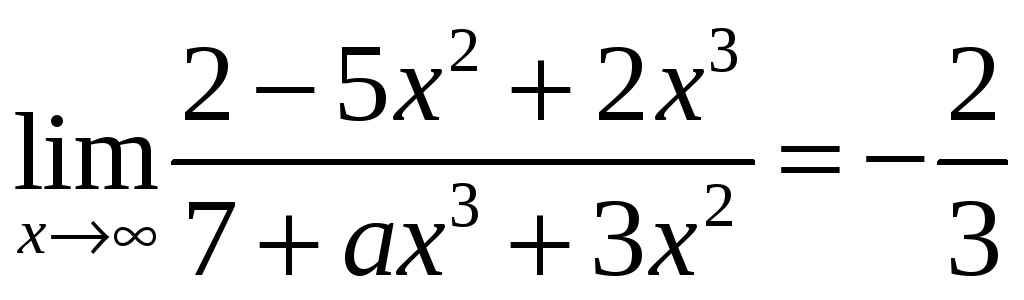 ,
то значение параметра
,
то значение параметра
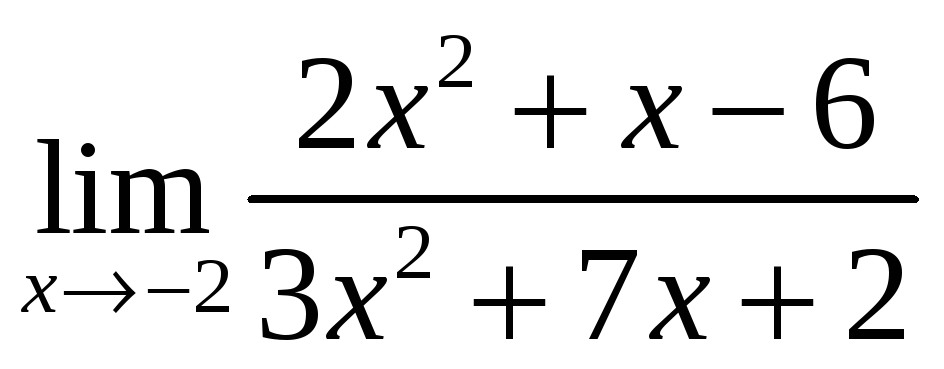 равен:
равен: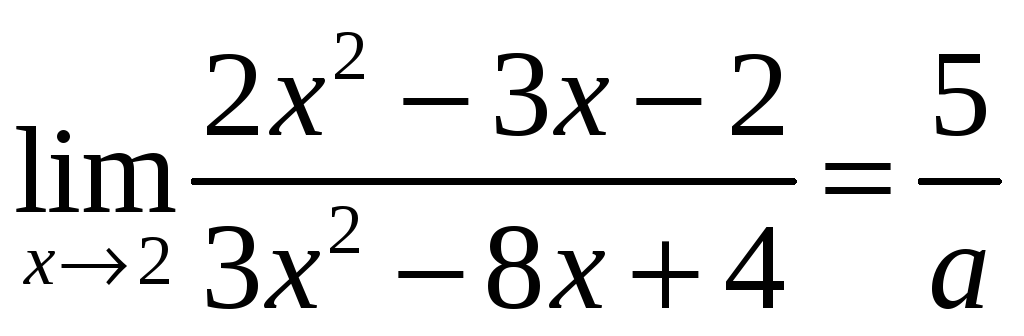 ,
где
,
где
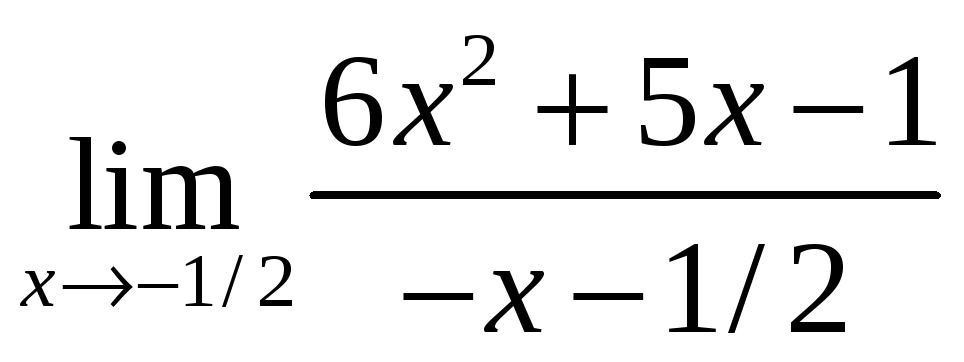 равен…
равен…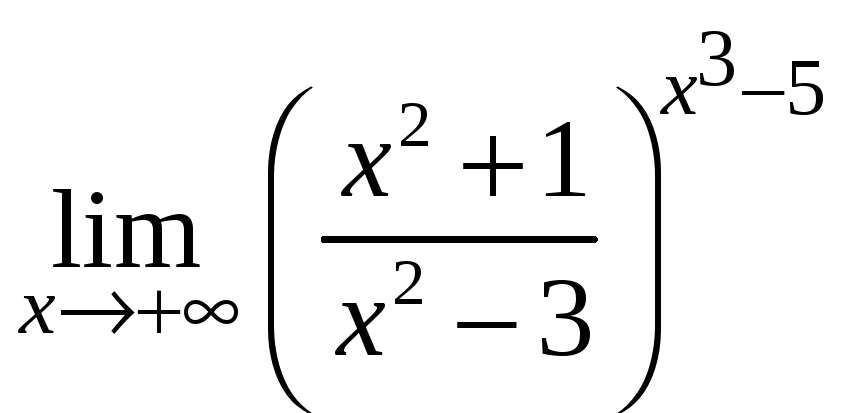 равен:
равен:
 ,
где
,
где
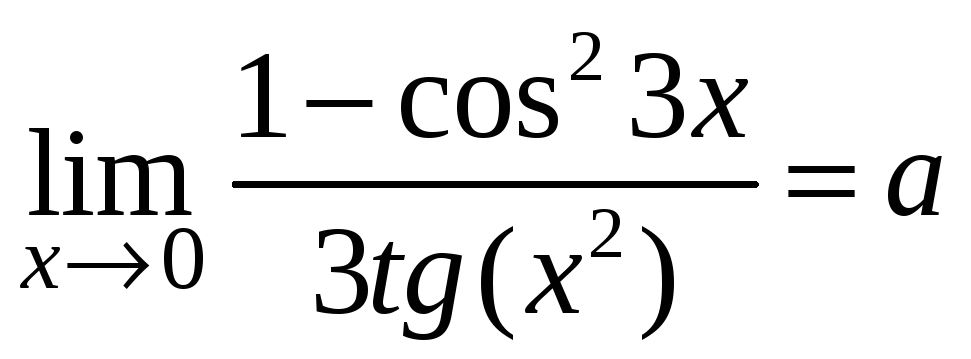 ,
где
,
где
 ,
где
,
где
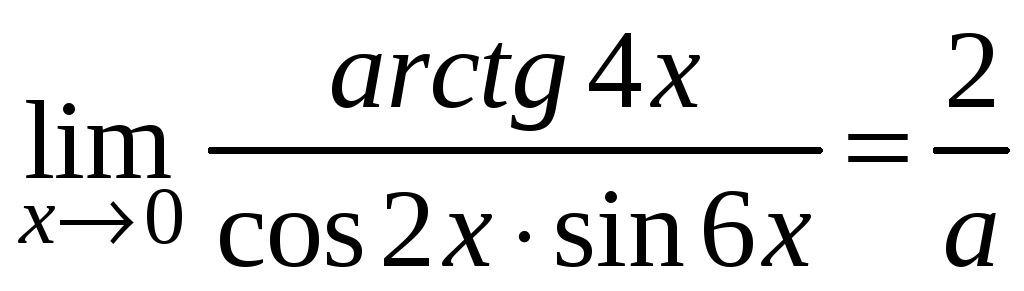 ,
где
,
где
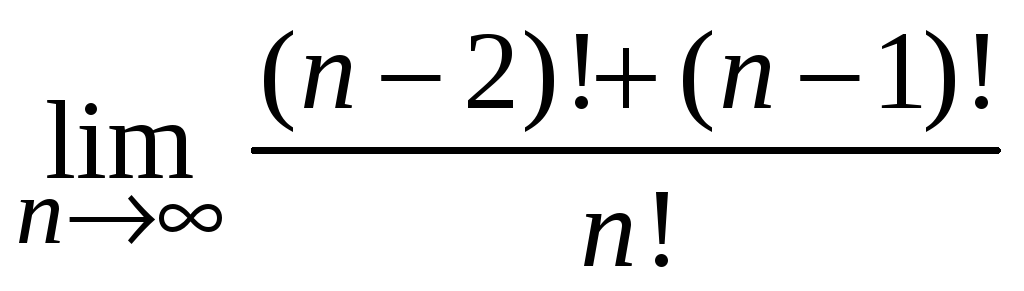 равен:
равен: ,
где
,
где
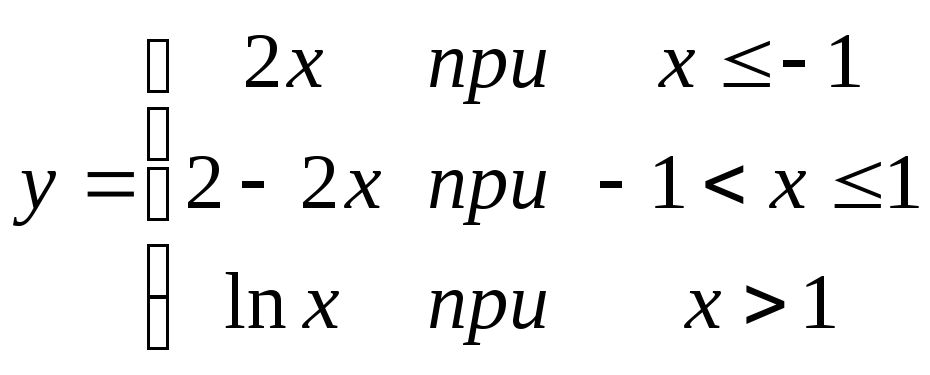 и В:
и В: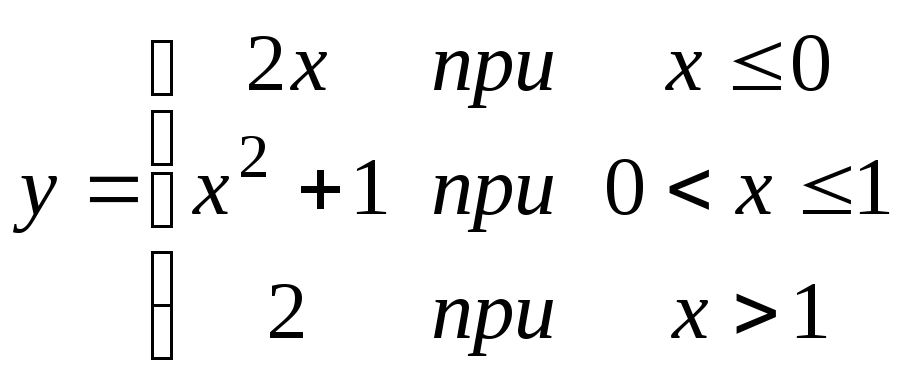 .
.
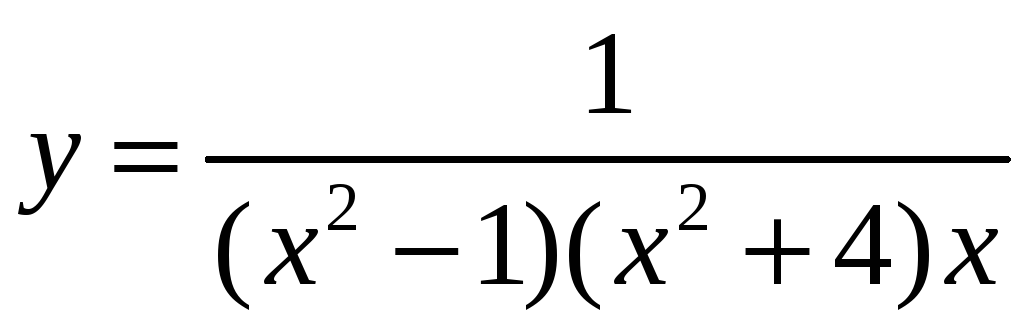 .
Точками её разрыва из перечисленных
ниже точек являются:
.
Точками её разрыва из перечисленных
ниже точек являются:
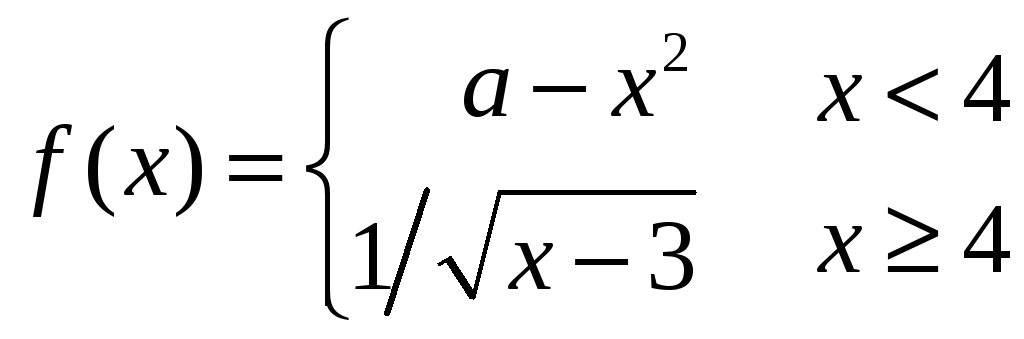 будет непрерывной в точке
будет непрерывной в точке
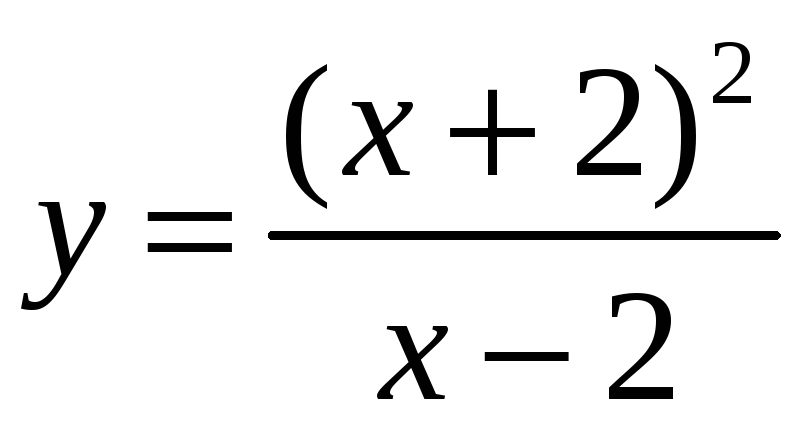 2)
2)
 3)
3)
 4)
4)
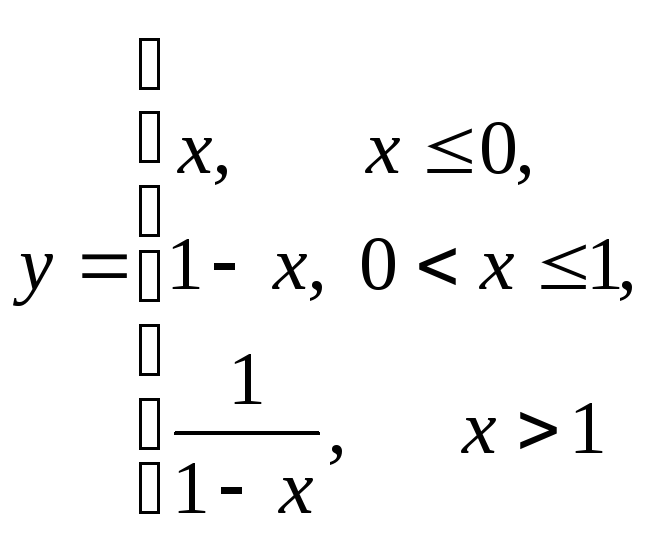 B:
B:

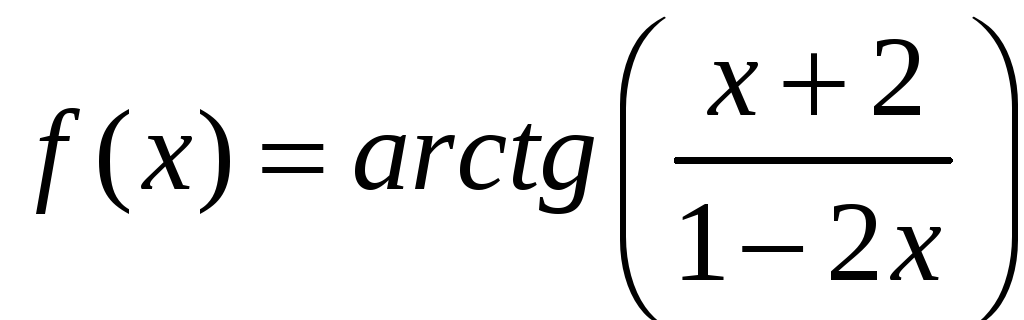 имеет вид:
имеет вид: 2)
2)
 3)
3)
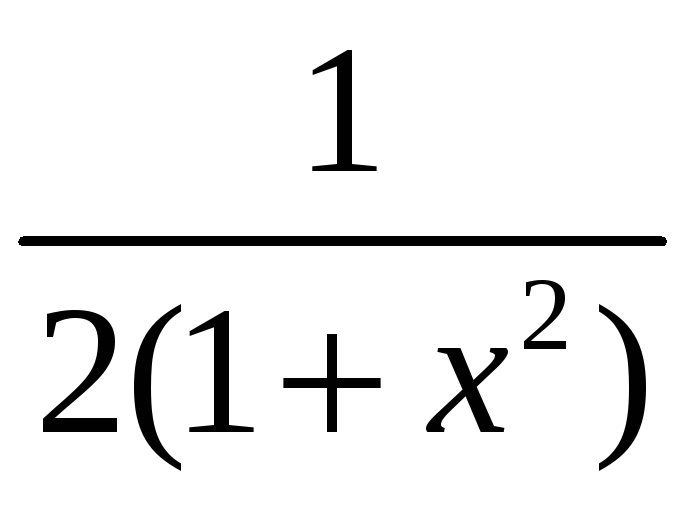 4)
4)
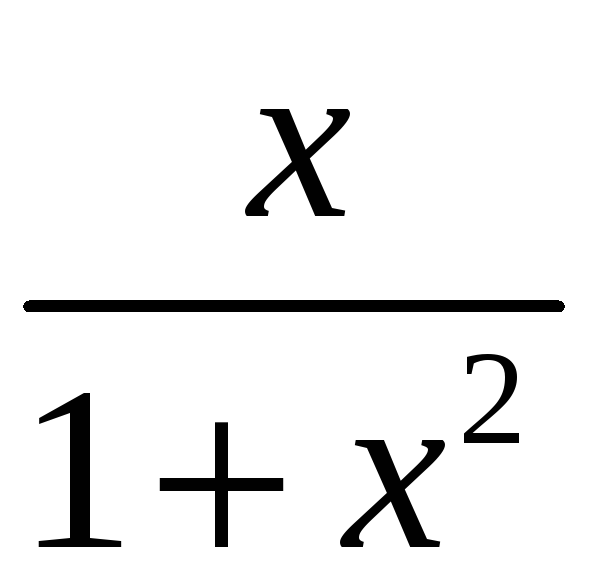 5)
5)

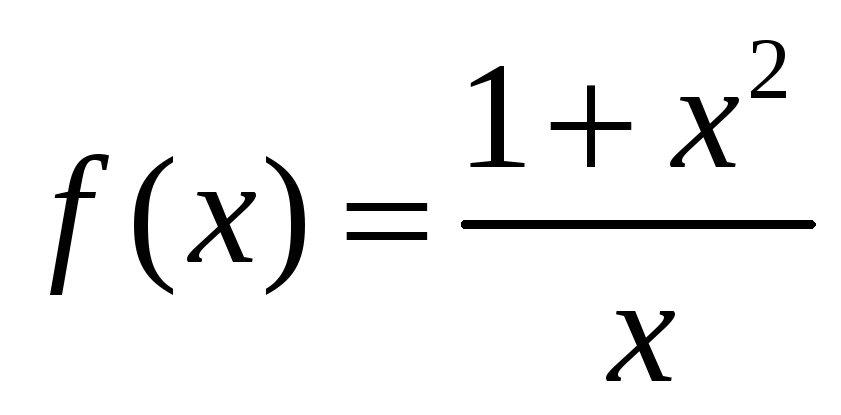 1:
1:

 2:
2:
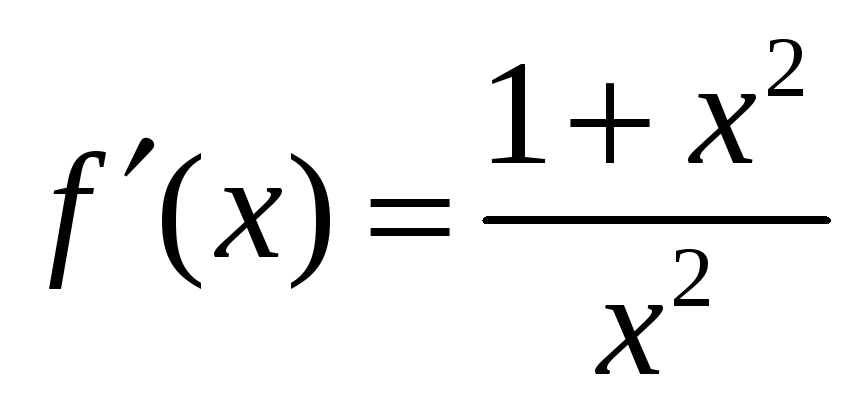
 3:
3:

 ,
где
,
где
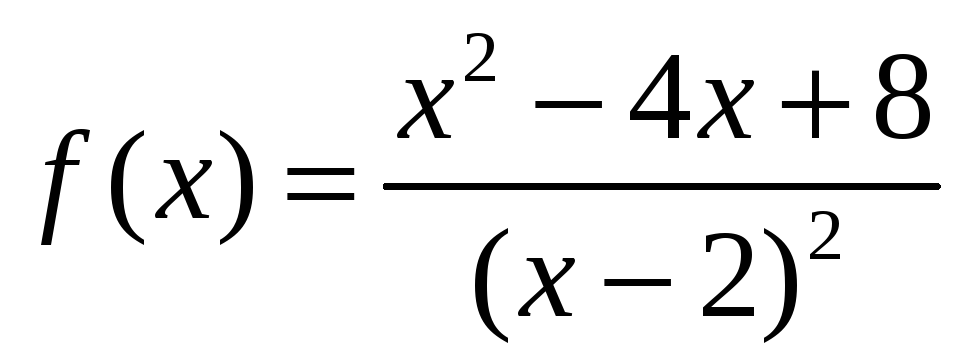 ,
то значение её первой производной
,
то значение её первой производной
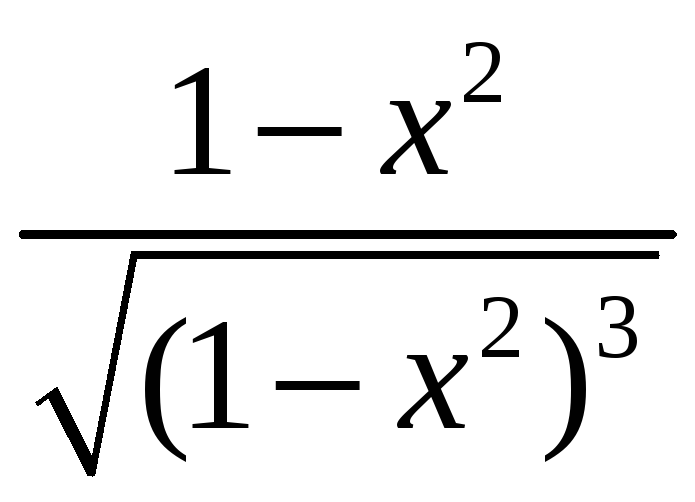 2)
2)
 3)
3)
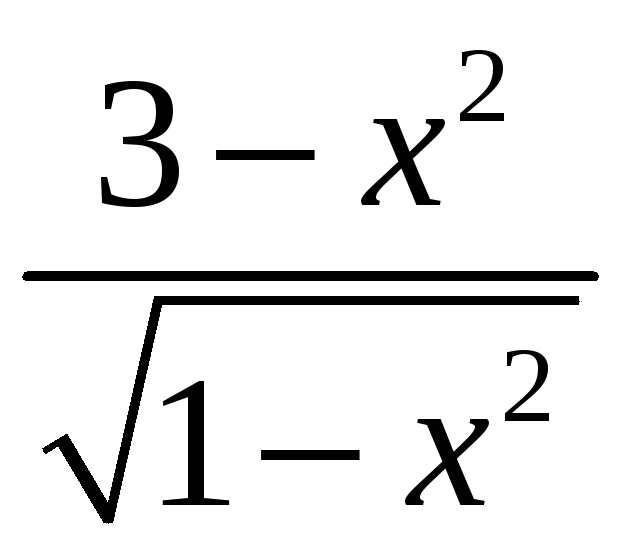 4)
4)
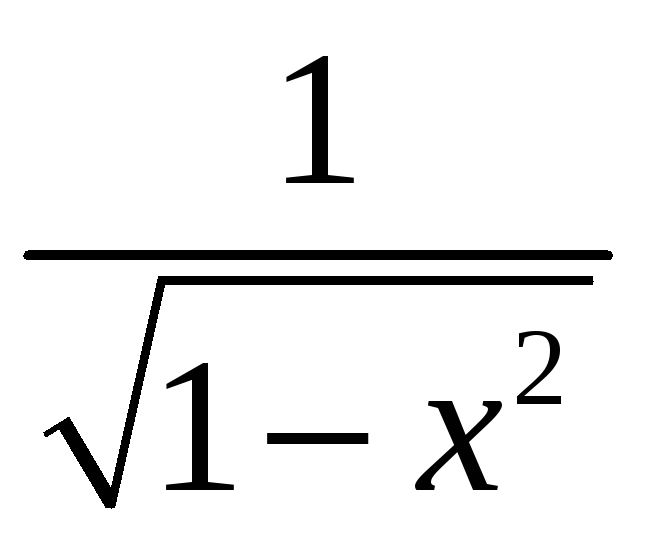 5)
5)
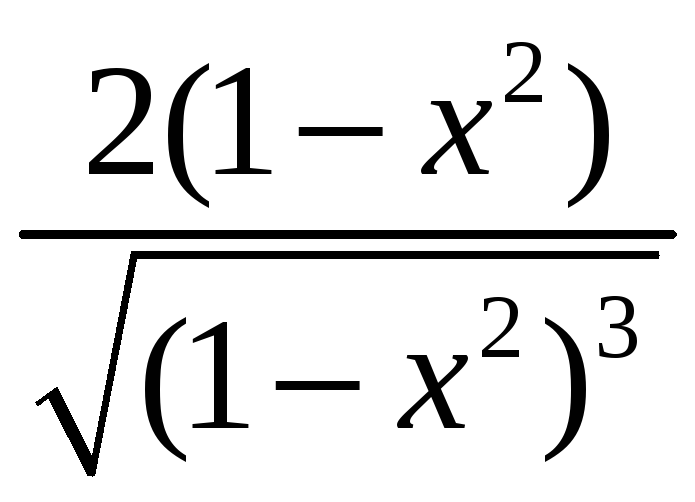
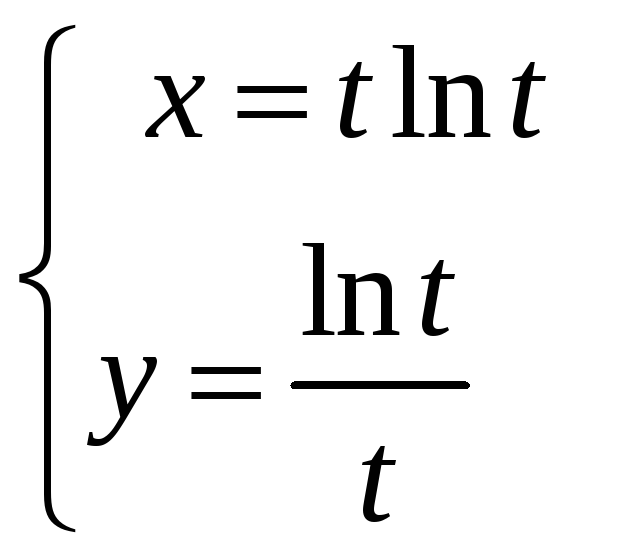 ,
то её параметрическая производная
,
то её параметрическая производная
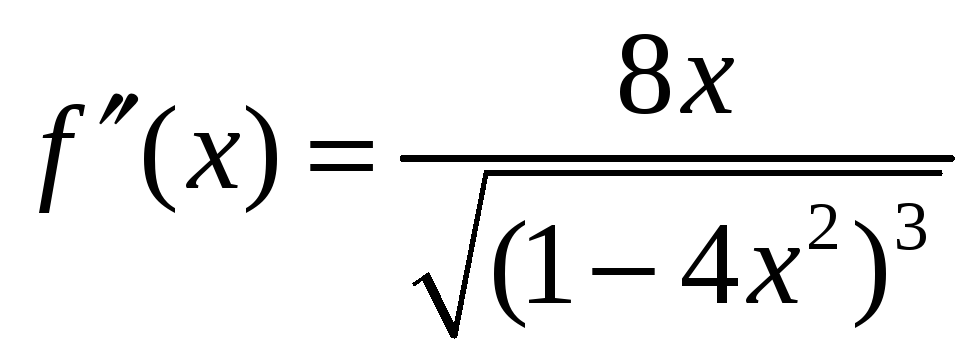 2:
2: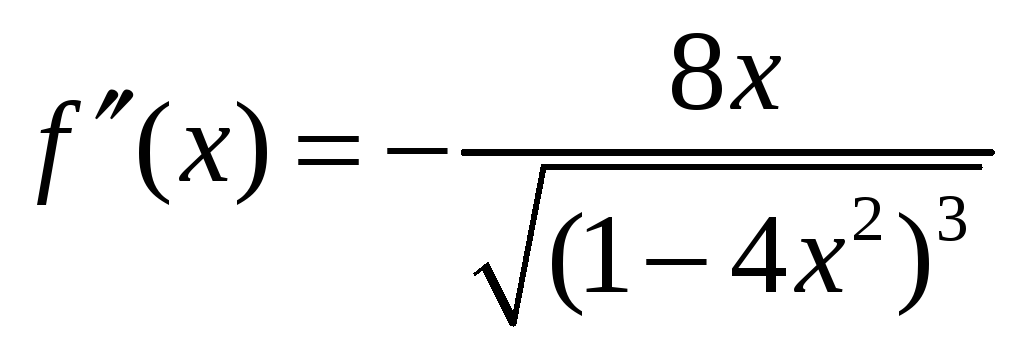 3:
3:

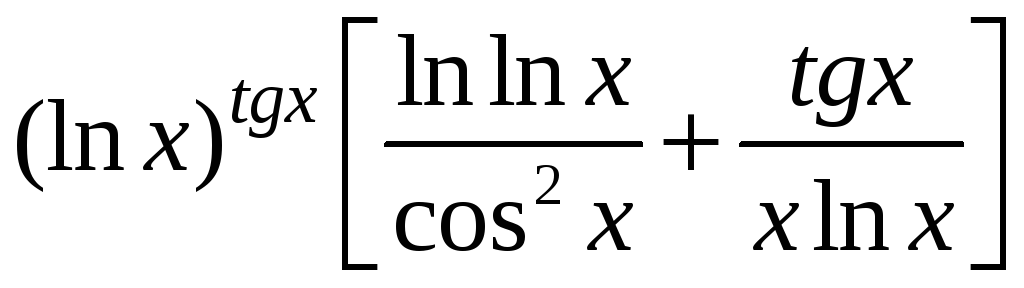 2)
2)
 4)
4)
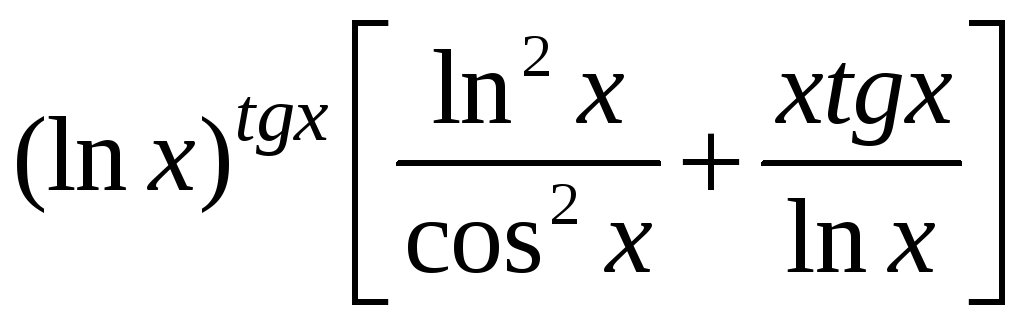
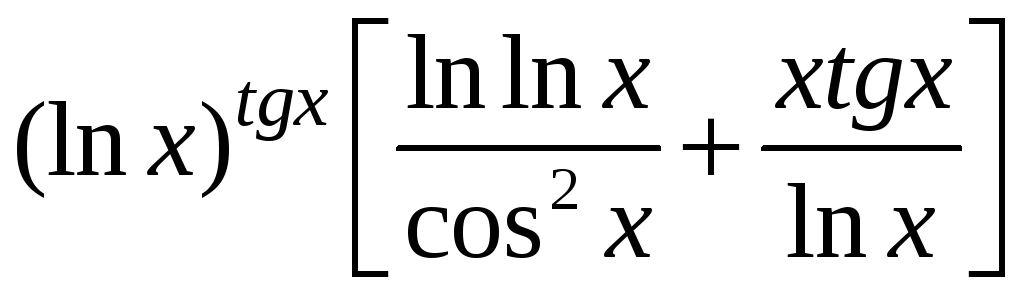
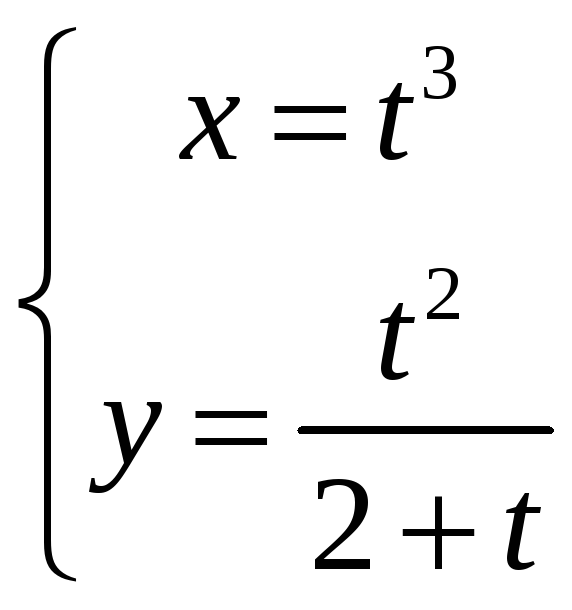 в точке,
соответствующей
значению параметра
в точке,
соответствующей
значению параметра
 на отрезке
на отрезке
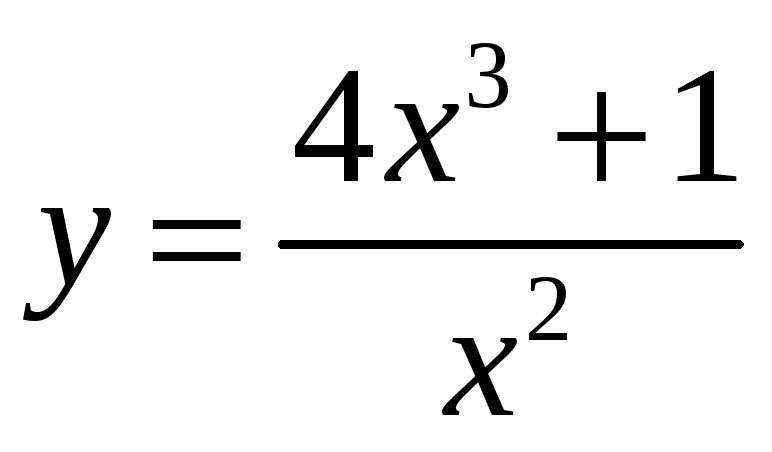 является прямая
является прямая
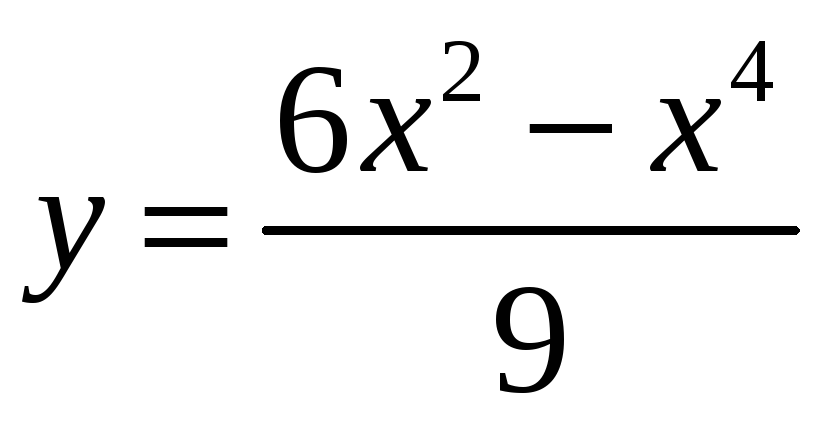 является интервал
является интервал
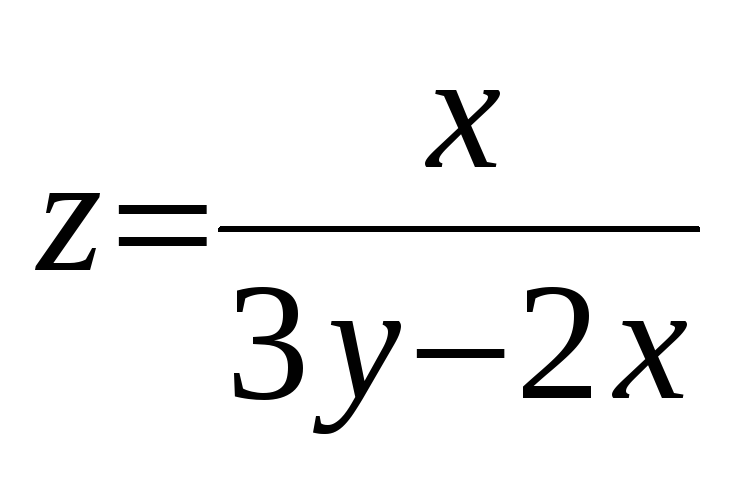 в точке
в точке
 ,
где
,
где
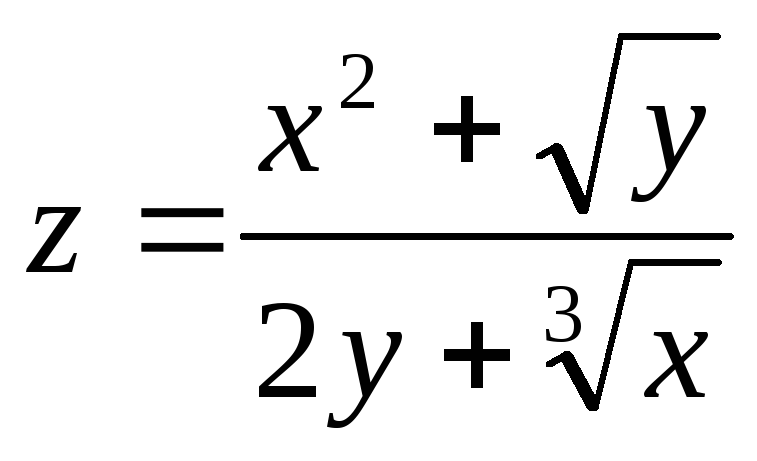 в
точке
в
точке