
36 Методическое изучение степенной функции
.docx-
Обобщение понятия степени
-
Актуализация знаний о степенных функциях изученных в основной школе
-
Методика изучения степенной функции в курсе алгебры и начала анализа
-
В курсе алгебры 7 класса учащиеся знакомятся с натуральным показателем степени
Опр.
A7 класса:
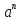 =a*a*a*…*a
=a*a*a*…*a
A8
класса определение в нулевой степени
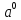 =1,
a≠0
=1,
a≠0
A8
определение в отрицательной степени
 =1/
=1/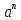
A9 класса определение степени с рациональным показателем
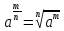 m,n-
натуральные числа, а≥0
m,n-
натуральные числа, а≥0
Свойства степени
-
 a>0
m,n-целые
числа n,q-
натуральные числа
a>0
m,n-целые
числа n,q-
натуральные числа -

-
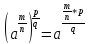
-
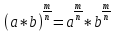
-
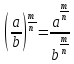 a>0
b>0
a>0
b>0
-
В связи с расширением понятия степени в основной школе учащиеся уже знакомятся с некоторыми степенными функциями, например заданными некоторыми формами
А) y=x˚ x≠0 изобразить
Это прямая параллельная оси ОХ где точка (о;1) выбита
Б)
у=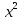 парабола
парабола
В)
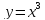
Г)
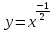
Д)
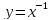
Е)
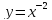 или
или
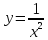
-
Функция вида
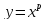 ,
где р- заданное действительное (число
называется степенной функцией.
,
где р- заданное действительное (число
называется степенной функцией.
Рассмотрим виды степенных функций и их свойства.
Если
p=2n-
четное число.
В этом случае степенной функцией
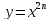 обладает следующими свойствами
обладает следующими свойствами
-
Область определения все действительные числа
-
Множество значений все неотрицательные числа (от 0 включительно и до +бесконечности)
-
Четная
-
Функция убывает от (-∾;0] возрастает [0; +∾)
-
Непрерывная
-
Ограниченна снизу
-
Ymin=0 при x=0
Ymax- не имеет
Если p=2n-1 - четное число
В этом случае степенная функция обладает следующими свойствами
-
Область определения множество действительных чисел
-
Область значений множество действительных чисел
-
Нечетная
-
Возрастает на всей действительной оси
-
Непрерывна
-
Не ограниченная
-
Максимума и минимума не существует
Если p=-2n, где k натуральное число
-
Область определения множество действительных чисел кроме 0
-
Множество значений y>0
-
Нечетная
-
Возрастает на промежутке где x˂0, убывает на х>0
Если p=-(2n-1), где n-натуральное число.
-
область определения (-∾;0) (0; +∾)
-
множество значений (-∾;0) (0; +∾)
-
нечетная
-
функция является убывающей на промежутках x˂0 и х>0
-
неограниченная
-
не убывает
-
асимптота х=0
Показатель р- положительное действительное целое число. В том случае функция обладает следующими свойствами
-
область определения- неотрицательные числа х≥0
-
множество значений- неотрицательные числа у≥0
-
функция является возрастающей на промежутке х≥0
-
область определения непрерывна
-
ограничена у=0
-
ymin в точке (0,0)
Показатель р- отрицательное действительное не целое число. В том случае функция обладает следующими свойствами
-
область определения (0; +∾)
-
множество значений (0; +∾)
-
функция является убывающей на (0; +∾)
-
непрерывная
-
при х→+∾, у→0
-
при х→0, у→+∾
