165. If two random variables X and y have the joint density function, , find the conditional pdf.

• 

166. If two random variables X and y have the joint density function, , find the conditional pdf.

• 

167. A basketball player makes 90% of her free throws. What is the probability that she will miss for the first time on the seventh shot?

• 0.053

168. The joint distribution for two random variables X and Y is given by . Then find P(Y>0.5).

• 0.5

169. Let X be a continuous random variable with probability density given by . Let Y=2X-3. Find P(Y≥4).

• 0.53125

170. Random variable X has the following PDF

Find .

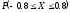• 0.512

171. Random variable X has the following PDF

Find E[X].

• 0

172. Random variable X has the following PDF

Find Var[X].

• 0.6

173. Random variable X has the following PDF

Find .

• 0

174. The joint distribution for two random variables X and Y is given by . Find the marginal density function for X.

• 3x²

175. The joint distribution for two random variables X and Y is given by . Find the marginal density function for Y.

• 2y

176. The joint distribution for two random variables X and Y is given by 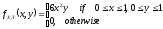. Find the E[X].

• 0.75

177. The joint distribution for two random variables X and Y is given b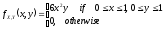y . Find the E[Y].

• 2/3

178. Assume that Z is standard normal random variable. What is the probability P(|Z|>2.53)?

• 0.0114

179. If Z is normal random variable with parameters µ=0, σ²=1 then the value of c such that P(|Z|<c)=0.7994 is

• 1.28

180. The random variable X has the continuous CDF

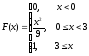. Find P(2≤X≤4).

• 5/9

181. Let X be the random variable for the life in hours for a certain electronic device. The probability density function is

. Find the expected life for a component.

• 2000 hours

182. The joint distribution for two random variables X and Y is given by . Find E[X-Y].

• 0

183. The joint distribution for two random variables X and Y is given by . Find E[X+Y].

• 7/6

184. The joint density function for the random variables X and Y is given by . Find E[X].

• 1

185. A box contains 15 balls, 10 of which are black. If 3 balls are drawn randomly from the box, what is the probability that all of them are black?

• 0.26

186. The Cov(aX,bY) is equal to

• 

187. If A and B are two mutually exclusive events with P(A) = 0.15 and P(B) = 0.4, find the probability P(A and B^c) (i.e. probability of A and B complement).

• 0.15

188. From a group of 5 men and 6 women, how many committees of size 3 are possible with two men and 1 woman if a certain man must be on the committee?

• 

189. Let ,,, be the joint PDF of X and Y. Find the marginal PDF of Y.

• y+1/2

190. Let ,,, be the joint PDF of X and Y. Compute E[X].

• 0.823

191. Let ,,, be the joint PDF of X and Y. Compute E[Y].

• 0.823

192. Let ,,, be the joint PDF of X and Y. Compute E[2X].

• 7/6

193. Let X be continuous random variable with probability density function .Find the expected value of random variable X.

• 28/9

194. The joint distribution for two random variables X and Y is given by . Then find P(X>0.5).

• 0.25

195. Probability mass function for discrete random variable X is represented by the

graph. Find Var(X).

• 1

196. Two dice are rolled, find the probability that the sum is less than 13.

• 1

197. A bag has six red marbles and six blue marbles. If two marbles are drawn randomly from the bag, what is the probability that they will both be red?

• 5/22

198. A man can hit a target once in 4 shots. If he fires 4 shots in succession, what is the probability that he will hit his target?

• 175/256

199. Let random variable X be normal with parameters mean=5, variance=9. Which of the following is a standard normal variable?

• Z=(X-5)/3

Конец формы

1. A coin is tossed 6 times. What is the probability of exactly 2 heads occurring in the 6 tosses.

•