7 раб
.docМетодические рекомендации к выполнению практической работы №7.
Действия над комплексными числами в алгебраической и тригонометрической форме.
-
Понятие комплексного числа и его геометрическая интерпретация.
-
Действия над комплексными числами в алгебраической форме.
-
Тригонометрическая форма комплексного числа.
-
Действия над комплексными числами в тригонометрической форме.
1. Понятие комплексного числа и его геометрическая интерпретация.
Определение 1:
Комплексными числами называются числа
вида
,
где
и
- действительные числа, а число
,
определяемое равенством
,
называется мнимой единицей, если для
этих чисел понятия равенства и действия
сложения и умножения определены следующим
образом:
1). Два комплексных
числа
и
называются равными, если
,
;
2).
Суммой двух комплексных чисел
и
называется комплексное число
;
3).
Произведением двух комплексных чисел
и
называется комплексное число
;
Запись комплексного
числа в виде
называется
алгебраической
формой
записи комплексного числа, где
называется действительной
частью
комплексного числа, а
-мнимой
частью.
Пример1: 7+3i
Любое действительное
число содержится в множестве комплексных
чисел. Поэтому его можно записать так:
.
Пример: 4=4+0i
Определение 2:
Комплексное число
называется комплексно
сопряженным
с
числом
и
обозначается
,
то есть
.
Пример2: 2+5i и 2-5i
Определение 3:
Модулем
комплексного числа
называется число
:
.
Причем
.
Комплексное число можно изобразить двумя способами:
1. Точкой плоскости с координатами (а;в).
При этом действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а чисто мнимые числа- точками оси ординат, которую называют мнимой осью.
2. В виде вектора
с началом в начале координат (
)
и концом в точке М(а;в) (
).
Каждой точке
плоскости с координатами (а;в) соответствует
один и только один вектор с началом в
точке О(0;0) и концом в точке М(а;в),поэтому
комплексное число
можно изобразить в виде вектора
.
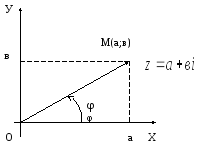
Определение 4:
Угол φ
между действительной осью ОХ и вектором
,
отсчитываемый от положительного
направления действительной оси,
называется аргументом
комплексного числа. Если отсчет ведется
против движения часовой стрелки, то
величина угла считается положительной,
иначе- отрицательной.
Любое комплексное
число имеет бесконечное множество
аргументов, отличающихся друг от друга
на число, кратное
.
Наименьшее по абсолютной величине
значение аргумента из промежутка
называется главным
значением аргумента.
Из определения тригонометрических функций следует:
Пример3:
Изобразить геометрическую интерпретацию комплексного числа, найти модуль комплексного числа и главное значение аргумента.
а).
;
б).
;
в).
.
Решение:
а).
;
б).
;
в).
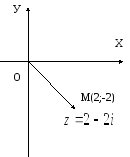
2. Действия над комплексными числами в алгебраической форме.
Сложение и умножение
комплексных чисел мы ввели в определении
комплексного числа. Введем правила
вычитания и деления комплексных чисел:
;
.
Но удобнее всего действия над комплексными числами производить с помощью правил соответствующих действий над многочленами и понятием мнимой единицы.
Пример4:
Выполнить действия:
а).
;
б).
;
в).
;
г).
;
д).
;
е).
;
ж).
;
з).
;
и).
;
к).
.
Решение:
а).
;
б).
;
в).
;
г).
;
д).
;
е).
;
ж).
;
з).
;
и).
;
к).
.
3. Тригонометрическая форма комплексного числа.
Изобразим комплексное
число
геометрически:
Обозначим модуль
комплексного числа
.
Аргументом комплексного числа называется угол φ, который вычисляется с помощью формул:
но
,
тогда
и
Подставим
получившиеся формулы в
,
получим:
,тогда
-
тригонометрическая форма комплексного
числа.
Алгоритм перехода из алгебраической формы комплексного числа в тригонометрическую:
-
Найти:
. -
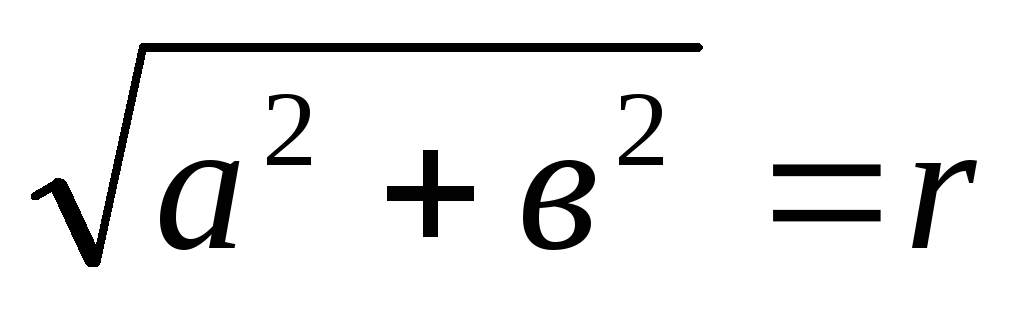Изобразить геометрически число
,
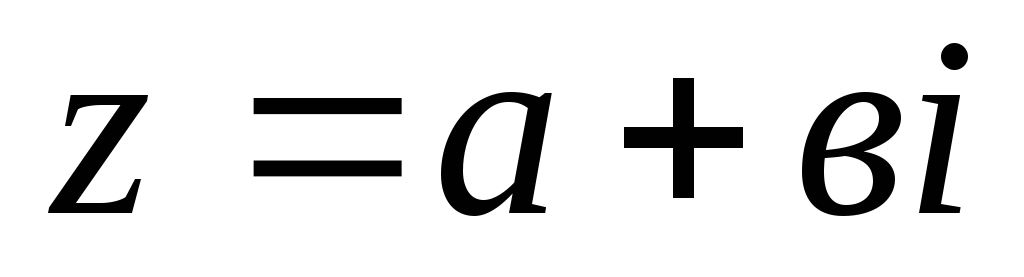для нахождения четверти числа φ. -
Составить уравнения:
и найти φ. -
Записать z в тригонометрической форме
.
Примеры: а).Перевести числа из алгебраической формы в тригонометрическую.
1).
.
1.
.
2. Изобразим геометрически:
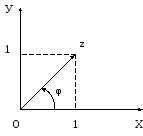
Значит φ принадлежит I четверти.
3.
.
4.
.
2).
.
1.
.
2. Изобразим геометрически:
,
так как z
принадлежит положительной полуоси ОУ.
Значит 3 пункт можно опустить.
4.
.
3).
1.
.
2. Изобразим геометрически:
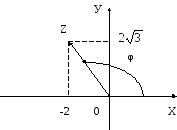
φ принадлежит II четверти.
3.
.
4.
б). перевести из тригонометрической формы в алгебраическую:
1).
Решение:
.
2).
Решение:
.
4. Действия над комплексными числами в тригонометрической форме.
Пусть даны два
числа в тригонометрической форме:
и
.
1). При умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:
.
2). При делении двух комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются:
.
3). При возведении
комплексного числа
в
n-ую
степень используется формула:
,
которая называется формулой Муавра.
4). Для извлечения
корня n-ой
степени из комплексного числа
используется формула:
.
Примеры:
Дано:
,
.
Найти: 1).
,
2).
,
3).
,
4).
.
Решение: 1).
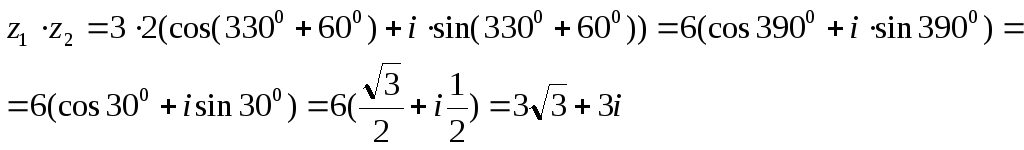
2).
3).
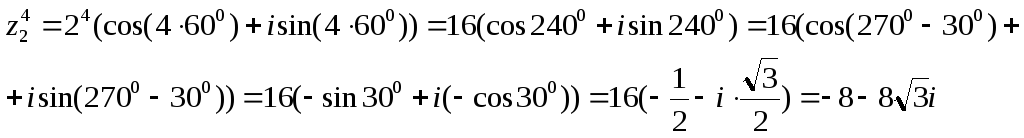
4).
Практическая работа№7.
Тема: Действия над комплексными числами в алгебраической и тригонометрической форме.
Цель: Научить выполнять различные действия с комплексными числами; переводить комплексные числа из алгебраической формы и обратно;
Задания:
I-B II-B
1. Выполнить действия с комплексными числами в алгебраической форме:
1
).
,
1).
,
2).
,
3).
.
2).
,
3).
.
2. Записать комплексные числа в тригонометрической форме:
1).
,
2).
,
3).
.
1).
,
2).
,
3).
.
3. Выполнить
действия с комплексными числами в
тригонометрической форме: 1).
, 2).
,
если:
,
,
.
.
Ответы к практической работе № 6:
I-B. II-B.
1
.
1).
,
1. 1).
2).
,
2).
,
3).
.
3).
.
2. 1).
,
2. 1).
,
2).
,
2).
,
3).
.
3).
.
3. 1).
,
3. 1).
,
2).
.
2).
.