Лабораторная работа №2 Математические расчеты в MathCad
Цель работы
Овладеть навыками работы с ранжированными переменными и функциями в MathCAD.
Задачи:
- умение вводить ранжированные переменные и функции в Mathcad;
Порядок выполнения
Задание №1:
Ввести ранжированную переменную d на отрезке [-2;1] с шагом 0.2.
Ранжированная переменная – это особый вид переменной, которая может принимать множество значений. Она определяется начальным и конечным значениями, а также шагом изменения значения.
Для определения ранжированной переменной необходимо выполнить следующее:
1. Ввести имя ранжированной переменной: а:=
2. Указать начальное значение переменной, например -5
3. Через запятую ввести следующее значение переменной -5, -4.5 т.е. шаг получается 0.5
4. Вставить символ ; и конечное значение переменной, например 5.
5. Нажать Enter.
6. Чтобы увидеть значения созданной ранжированной переменной, необходимо набрать: d= (рис. 7).
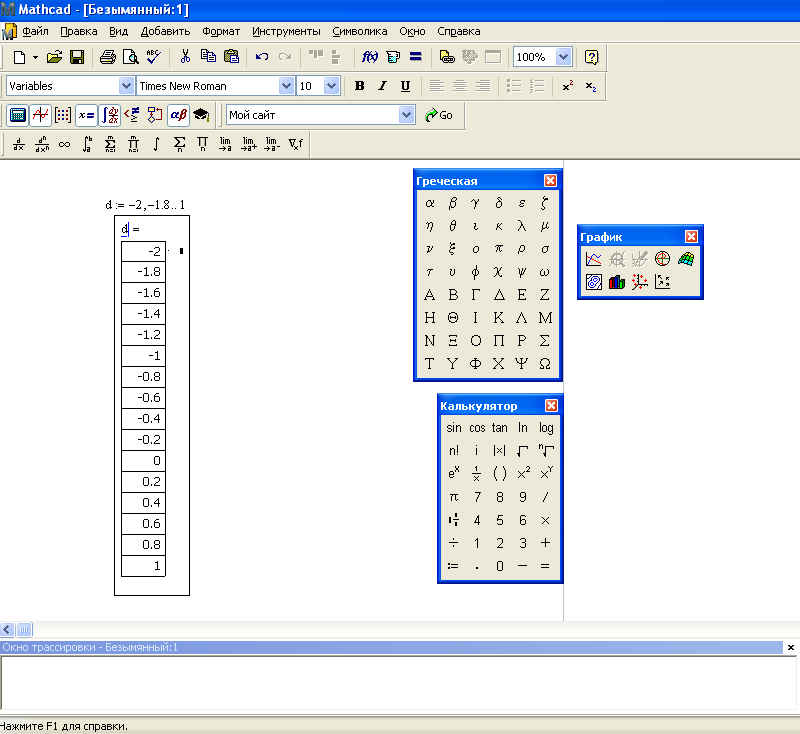
Рис 7. Создание ранжированной переменной
Самостоятельно:
1. Ввести ранжированную переменную а на отрезке [-4;1] с шагом 1.
2. Ввести ранжированную переменную h на отрезке [-7;7] с шагом 1.5.
Задание №2:
Определить функцию от нескольких переменных.
Функции используемые в Mathcad делят на встроенные и определенные пользователем.
Функции можно вставить как с клавиатуры так и с помощью мастера функций.
Таблица 1
Описание функций
-
Функция
Описание функции
Функции для работы с комплексными переменными:
Re(z)
Действительная часть комплексного числа z
Im(z)
Мнимая часть комплексного числа z
arg(z)
Аргумент комплексного числа
csng(z)
Функция вычисления знака комплексного числа
Функции теории чисел и комбинаторики
combin(n,k)
число сочетаний из kэлементов поn
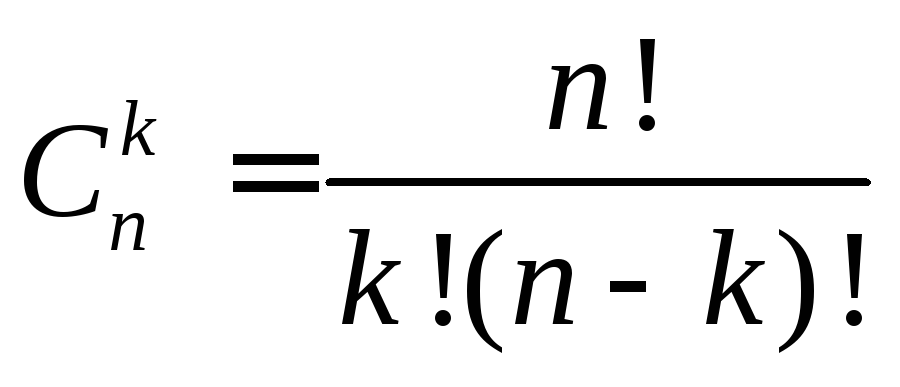
permut(n,k)
число размещений из kэлементов поn
gcd(a,b,c,d,…)
наибольший общий делитель у набора чисел a,b,c,d
lcm(a,b,c,d,…)
наименьшее общее кратное у набора чисел a,b,c,d
mod(x,y)
вычисляет остаток от деления xнаy
Основные строковые функции
concat(s1,s2,s3,…)
формирует строку как объединение строк s1,s2,s3,…
error(s)
строка sвозвращается как сообщение об ошибке
IsString(s)
возвращает: 1 если s– строка,
0 в других случаях
num2str(z)
преобразовывает комплексное или действительное число zв строку
search(s,subs,m)
возвращает номер позиции первого вхождения подстроки subsв строкуsначиная с позицииm
str2num(s)
преобразовывает строку в число
str2vec(s)
возвращает вектор, i-й элемент которого являетсяASCII– кодомi-го символа строки
Существует возможность определять новые функции как одного, так и нескольких аргументов
1. необходимо указать имя функции;
2. в скобках перечислить аргументы;
3. набрать «:=» и определить новую функцию
Например:
Найти значение функций:
1.
f(1.3)=__
2.
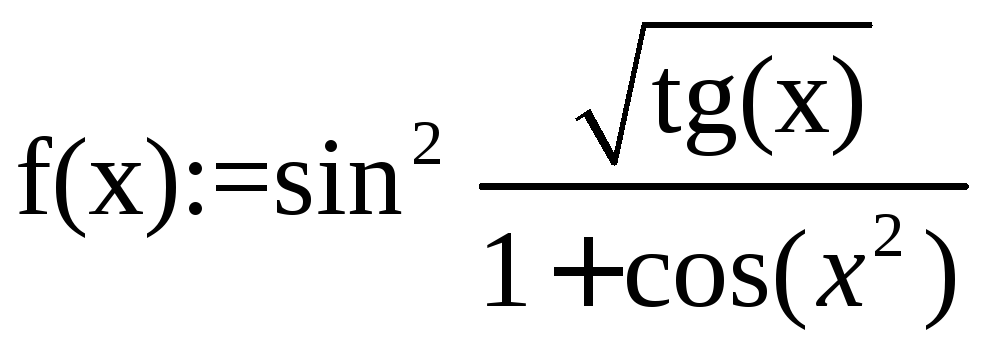
h:=-
,
3.
g(4,2)=__
4.
g(0,1)=__
Ответы:
1. f(1.3)=0.623
2.
3. g(4,2)=-4.017*10-3
4. g(0,1)= -0.189
Задание №3:
С помощью функции If, вывести сообщение, положительное или отрицательное число.
Структура функции If: if (условие, значение1, значение2). Функция возвращает значение1, если условие истинно или значение2 в противном случае.
Например:
x:=-10
if(x<0, «отрицательное», «положительное»)= «отрицательное» (рис. 8)
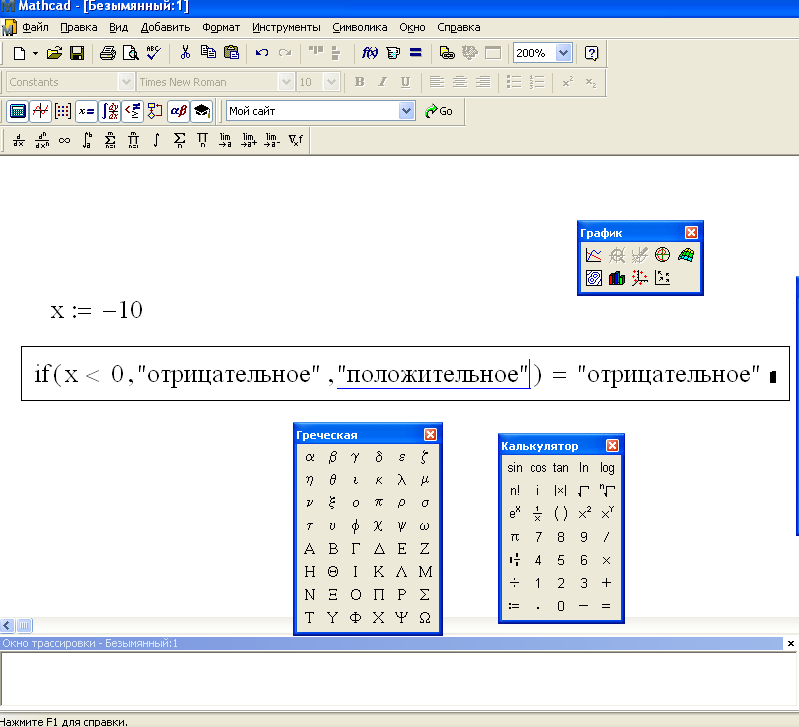
Рис 8. Оператор условия
Задание №4:
При помощи функций
чисел и комбинаторики вычислить:
,
В меню выбрать: Добавить – Функция и в появившемся диалоговом окне выбрать категорию и имя функции ( рис.9)
Рис 9. Вставка функции