
Raschetgraf00 геодезия
.pdf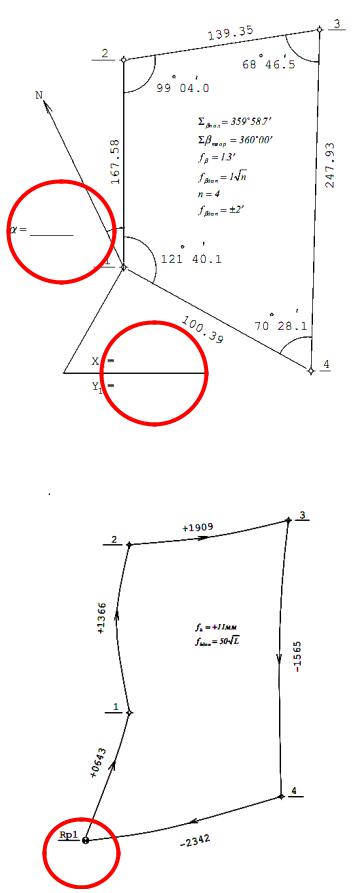
200° 10.5′
235.10
235.10
Рис. 2 - Исходные данные для теодолитного хода
3) Вписать отметку исходного репера в схему нивелирного хода, стр. 10 бланка РГР, рис. 3.
150.210
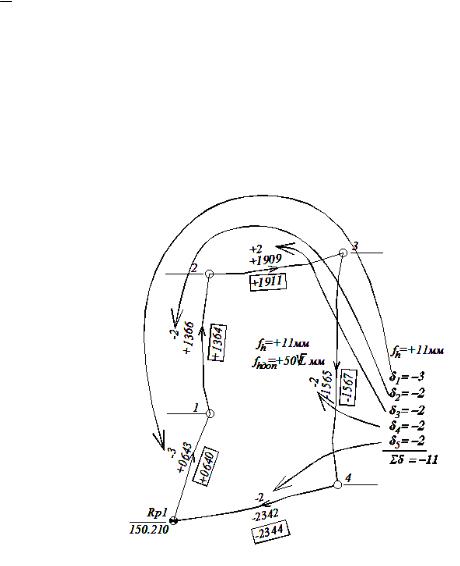
Рис. 3 - Исходные данные для нивелирования

4) Вычислить измеренные углы и средние расстояния в журнале измерения углов, бланк РГР стр.7.
Каждый горизонтальный угол измерен дважды при двух положениях вертикального круга теодолита (КЛ и КП). Углы в полуприемах вычисляются по формулам:
β |
КП |
= O ПЕРЕД − OЗАДН |
, |
(12) |
|
|
КП |
КП |
|||
β |
|
= O ПЕРЕД − OЗАДН |
|||
КЛ |
|
|
|||
|
КЛ |
КЛ |
|
|
|
где βКЛ, βКП - углы при двух положениях (КЛ и КП) вертикального круга теодолита; OКЛ• ПЕРЕД , OКЛ• ЗАДН - отсчеты по теодолиту при положении вертикального круга КЛ при наведении на переднюю и заднюю точки; OКП• ПЕРЕД , OКП• ЗАДН - отсчеты по теодолиту при положении вертикального круга КП при наведении на переднюю и заднюю точки.
Если разность вычисленных углов в полуприемах не превышает 1′ , то вычисляют средние значения измеренных углов β = 0.5(β КП + β КЛ).
Таблица 1 – Журнал измерения горизонтальных углов
дата 19.01.2020
исполнитель Иваненко В. В.
Точка ус- |
Точка визи- |
Отсчет по гори- |
Измеренный |
Средний угол |
Расстояние |
тановки |
рования |
зонтальному кругу |
угол |
|
|
теодолита |
|
|
|
|
|
|
1 |
100 18.5 |
|
|
1-2 |
2КЛ |
|
|
99 04.5 |
|
167.55 |
|
3 |
1 14.0 |
|
99 04.0 |
167.61 |
|
1 |
189 43.0 |
|
|
167.58 |
2КП |
|
|
99 03.5 |
|
|
|
3 |
90 39.5 |
|
|
|
|
2 |
93 21.5 |
|
|
2-3 |
3КЛ |
|
|
68 46.0 |
|
139.37 |
|
4 |
24 35.5 |
|
68 46.5 |
139.33 |
|
2 |
10 18.0 |
|
|
139.35 |
3Кп |
|
|
68 47.0 |
|
|
|
4 |
301 31.0 |
|
|
|
|
3 |
167 56.2 |
|
|
3-4 |
4КЛ |
|
|
70 28.2 |
|
247.97 |
|
1 |
97 28.0 |
|
70 28.1 |
247.89 |
|
3 |
111 15.0 |
|
|
247.93 |
4КП |
|
|
70 28.0 |
|
|
|
1 |
40 47.0 |
|
|
|
|
4 |
21 12.2 |
|
|
4-1 |
1КЛ |
|
|
121 40.2 |
|
100.37 |
|
2 |
259 32.0 |
|
121 40.1 |
100.41 |
|
4 |
165 42.5 |
|
|
100.39 |
1КП |
|
|
121 40.0 |
|
|
|
2 |
44 02.5 |
|
|
|
Вычисляются средние значения измеренных расстояний, допуск 1:2000, то есть разность прямых и обратных расстояний не должна превышать указанный допуск.
Результаты вычислений проверяются по значениям углов, приведенных на схеме теодолитного хода стр. 6 бланка РГР.
Дальнейшую обработку материалов осуществим исходя из принципа трудоемкости. То есть в первую очередь выполним более простые задания, затем – сложные.
5) Вычислить отметки точек теодолитного хода на схеме
хода
Работу начнем с вычисления отметок точек теодолитного хода на схеме нивелирования, стр. 10 бланка РГР. Прежде всего вычислим сумму измеренных превышений
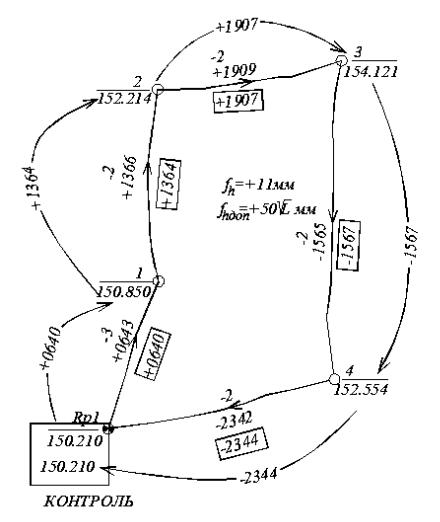
Σ h =+0643+1366+1909-1565-2342=+11мм.
Эта величина будет являться невязкой в превышениях fh = Σ h. После чего проверяется соответствие полученной невязки допуску:
fhдоп = 50
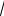 L , где L – длина хода в км. В нашем случае длина хода составляет 0.6км. Таким образом, допустимая невязка будет равна 39мм, а полученная – 11мм, следовательно, нивелирование выполнено верно. После диагностики полученной невязки вычисляем поправки в превышения и исправленные превышения δh = -fh/n, где n – число станций. Полученные поправки вводятся в измеренные превышения hисп = hпол + δh . Вычисление невязок и поправок показаны на рис. 4.
L , где L – длина хода в км. В нашем случае длина хода составляет 0.6км. Таким образом, допустимая невязка будет равна 39мм, а полученная – 11мм, следовательно, нивелирование выполнено верно. После диагностики полученной невязки вычисляем поправки в превышения и исправленные превышения δh = -fh/n, где n – число станций. Полученные поправки вводятся в измеренные превышения hисп = hпол + δh . Вычисление невязок и поправок показаны на рис. 4.
Рис. 4 – Вычисление поправок в превышения
После завершения вычисления исправленных превышений обязательно выполняется контроль Σhисп = 0.
Если сумма исправленных превышений равна нулю, то вычисляются отметки точек.
H |
1 |
= H |
Rp1 |
+ hИСПР |
; |
|||
|
|
|
Rp1−1 |
|
||||
H |
2 |
= H |
1 |
+ hИСПР; |
|
|||
|
|
|
|
|
1−2 |
|
||
H |
3 |
= H |
2 |
|
+ hИСПР; |
(13) |
||
|
|
|
|
|
2−3 |
|
||
H |
4 |
= H |
3 |
|
+ hИСПР; |
|
||
|
|
|
|
|
3−4 |
|
||
H |
Rp1 |
= H |
4 |
+ hИСПР. |
||||
|
|
|
|
4−Rp1 |
|
|||
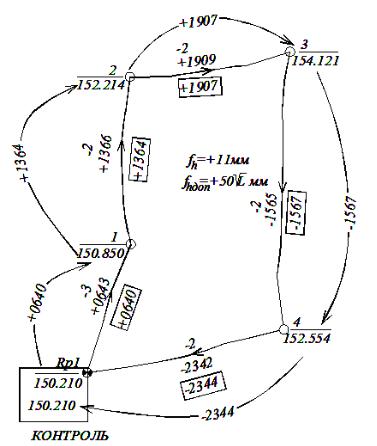
Ввычисления отметок показаны на рис. 5.
Рис. 5 – Вычисление отметок точек теодолитного хода
2.3. Обработка нивелирных журналов
Все нивелирные журналы обрабатываются аналогично, особенность обработки заключается только в вычислениях невязок в превышениях, методика вычисления которых зависит от вида хода. Так нивелирование точек теодолитного хода замкнутый нивелирный ход, опирающийся на одну исходную точку
Rp1. Невязка в превышениях fh вычисляется по формуле: |
|
fh = Σ hср , |
(13) |
где hср - среднее превышение.
Нивелирные хода при нивелировании по квадратам и нивелирование трассы представляют собой разомкнутые нивелирные хода, опирающиеся в первом случае на точки 2 и 3, во втором - на реперы Rp1 и Rp2. Невязка в пре-
вышениях для таких ходов будет равна: |
|
fh = Σ hср - (Нкон - Ннач), |
(14) |
где Нкон, Ннач - отметки, соответственно, начальной и конечной точек. Порядок обработки всех нивелирных журналов следующий.

1) Выполняются контрольные вычисления (постраничный контроль), для чего суммируются отдельно на каждой странице задние (Σ aзадн) и передние
(Σ bпередн) отсчеты, вычисленные (Σ hвычис) и средние (Σ hср) превышения. Контроль:
Σ aзадн - Σ bпередн = Σ hвычис;
Σ hвычис = 2Σ hср .
Результаты контроля записываются в соответствующих колонках, табл. 3.
Таблица 3 - Образец записи результатов постраничного контроля
№ |
№ |
|
Отсчеты по рейкам |
|
|
Превышения |
Отметки |
||||||||
ст |
тчк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
задн |
передн |
|
пром |
|
|
вычиc |
|
средн |
исправ |
ГИ |
точек |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
... |
|
....... |
....... |
|
..... |
|
....... |
...... |
..... |
..... |
..... |
|||
|
т 12 |
|
0635 |
2934 |
|
|
|
-2299 |
+2 |
|
123,755 |
123.120 |
|||
12 |
|
|
5417 |
7720 |
|
|
|
-2303 |
-2302 |
-2300 |
123,754 |
|
|||
|
т13 |
|
4782 |
4786 |
|
|
|
|
|
|
|
|
|
123,754 |
120.820 |
|
21 |
|
|
|
|
1235 |
|
|
|
|
|
|
|
|
122.519 |
|
22 |
|
|
|
|
1195 |
|
|
|
|
|
|
|
|
122.559 |
|
.. |
|
|
|
|
........ |
|
|
|
|
|
|
|
|
.... |
Контроль |
66052 |
70654 |
|
|
-4602 |
-2302 |
-2300 |
|
|
||||||
|
-70654 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
-4602 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fh = -3мм; |
|
|
|
||||||
|
|
|
|
f hдо п = 50 |
|
= 50 × |
|
|
= 70 мм. |
|
|
||||
|
|
|
|
L |
2 |
|
|
||||||||
2) Вычисляется невязка fh |
в превышениях |
|
|
|
|||||||||||
fh = Σ hср - |
для замкнутого нивелирного хода; |
|
|
||||||||||||
fh = Σ hср - (Hкон - Hнач) - для разомкнутого нивелирного хода. |
|
|||||
3) |
Проверяется соответствие вычисленной невязки величине допустимой |
|||||
невязке fh доп . |
|
|
|
|
|
|
fh доп = 50 |
|
|
|
- для нивелирования точек теодолитного хода и трассы; |
|
|
|
L |
|
||||
fh доп = 10 |
|
- для нивелирования по квадратам, |
|
|||
n |
|
|||||
где L - длина хода в км; n - число нивелирных станций. |
|
|||||
4) |
Вычисляются поправки δ h в превышения |
|
||||
|
|
|
|
|
δ h = -fh/n . |
(15) |
5) |
|
|
|
|
Контроль - Σδ h = - fh . |
|
Вычисляются исправленные превышения |
|
|||||
|
|
|
|
|
h иср = h сред + δ h . |
(16) |
Контроль - Σ h иср = (Hкон - Hнач) - для разомкнутого хода, Σ h иср = 0 - для замкнутого хода.
6) Вычисляются отметки связующих точек |
|
H = H0 + h иср , |
(17) |
где H0 - отметка предыдущей точки; H - отметка последующей точки. Контроль - вычисленная отметка исходной точки должна быть равна непосредственно отметке исходной точки.

7) После вычисления отметок всех связующих точек вычисляются отметки промежуточных точек. Для станций, имеющих промежуточные точки, вычисляется отметка горизонта инструмента
H ′ |
= H |
A |
+ a; |
ГИ |
= H |
(18) |
|
H ′′ |
|
||
B |
+ b, |
||
ГИ |
|
|
где HA - отметка задней по ходу связующей точки; HB - отметка передней по ходу точки; a - отсчет по задней точки; b - отсчет по передней точке.
|
H ′ |
− H ′′ |
|
≤ 5 , то вычисляется H |
|
= |
H ′ |
+ H ′′ |
|
Если |
|
|
ГИ |
ГИ |
. |
||||
|
ГИ |
|
|
||||||
|
ГИ |
ГИ |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
8) Вычисляются отметки промежуточных точек |
|||||||||
|
|
|
|
H = HГИ − с , |
|
(19) |
|||
где c - отсчет на промежуточной точке. |
|
|
|
|
|||||
Пример обработанных нивелирных журналов приведен в прил. 1.
5.2.3. Обработка журнала тахеометрической съемки При производстве тахеометрической съемки плановое положение точек
определяется полярным способом, высотное - тригонометрическим нивелированием.
Таблица 4 - Фрагмент журнала топографической съемки
№ |
Дальном. |
Отсчет |
Отсчет по |
МО |
Вертик |
Гориз |
h |
H |
Примечание |
точ |
расстоян |
по |
вертикал |
‘ |
угол |
проекция |
м |
м |
|
|
м |
горизон |
кругу |
|
° ‘ |
расстоян |
|
|
|
|
|
кругу |
° ‘ |
|
|
м |
|
|
|
|
|
° ‘ |
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Станция № 1 i=1.45 |
|
MO=+1’ |
|
Нстан=49,89 |
|
||||
|
|
|
|
|
|
|
|
|
Нземля =49.83 |
|
|
т4 |
100.39 |
0 00 |
0 59 Л |
|
1 |
|
0 58 |
100.39 |
+1.71 |
51.06 |
|
|
|
|
-0 57 П |
|
|
|
|
|
|
|
|
11 |
80.0 |
359 25 |
0 57 |
|
1 |
|
+0 56 |
80.0 |
+1.31 |
51.20 |
угол забора |
12 |
66.4 |
26 48 |
0 33 |
|
1 |
|
+0 32 |
66.40 |
+.061 |
50.50 |
граница пашни |
13 |
90.25 |
74 21 |
-0 03 |
|
1 |
|
-0 08 |
90.25 |
-0.21 |
49.68 |
обочина дороги |
Обработка журнала тахеометрической съемки выполняется в следующей последовательности.
1)Из журнала нивелирования точек теодолитного хода в журнал тахеометрической съемки, образец табл. 4, переписываются отметки станций.
2)Вычисляются вертикальные углы ν, используя для этих целей отсчеты по вртикальному кругу (Овер), колонка 4, и значение место нуля вертикального круга (МО), колонка 5,
ν = Овер - МО. |
(20) |
Вычисленные вертикальные углы ν записываются в колонку 6. |
|
3) Вычисляются горизонтальные проекции расстояний (S) |
|
S = DCosν, |
(21) |
где D - дальномерное расстояние, колонка 2; ν − вертикальный угол, колонка
6.
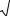
Если ν ≤ 3O , то S = D, в этом случае горизонтальные проекции расстояний приравнивают дальномерным расстояниям.
Горизонтальные проекции расстояний записываются в колонку 7 журна-
ла.
4) Вычисляются превышения
h = STg ν , (22)
Превышения записываются в колонку 8.
5) В колонке 9 записываются отметки всех пикетных точек, полученных по следующей формуле:
Hi = Hст + hi. |
(23) |
5.3. Вычисление координат точек теодолитного хода
На основе журнала измерения углов составлена схема теодолитного хода, прил. 1, включающая в себя измеренные углы, расстояния, техническую характеристику и исходные данные (координаты исходной точки и исходный дирекционный угол).
Вписывается в ведомость вычисления координат, образец табл. 5, из расчетной схемы номера точек (колонка 1), измеренные углы (колонка 2), измеренные расстояния, приведенные к горизонту (колонка 5).
Вычисляется сумма измеренных углов
Σβ ПОЛ = ΣβИЗМ . |
(24) |
Контролем правильности измерений и предварительных вычислений уг- |
|
ловых измерений является выполнение следующего условия: |
|
Σβ ПОЛ = ΣβТЕОР , |
(25) |
где Σβ п о л - полученная сумма измеренных горизонтальных углов; Σβ теор |
- теоре- |
тическая сумма горизонтальных углов. Для замкнутого теодолитного хода она равна
Σβ ПОЛ = 180(n − 2) , |
(26) |
где n - число внутренних углов теодолитного хода.
Разность полученной и теоретической сумм углов образуют угловую невязку f β
fβ = Σβ ПОЛ − ΣβТЕОР , |
(27) |
величина, характеризующая качество угловых измерений. Вычисленная угловая невязка не должна превышать допустимую
fβдоп = 1 |
n |
. |
|
|
(28) |
Если угловая невязка не превышает допустимую, то вычисляются по- |
|||||
правки в измеренные углы |
|
||||
δ β = − |
fβ |
. |
(29) |
||
|
|||||
|
|
|
n |
|
|
Сумма поправок должна равняться угловой невязке, взятой с противоположным знаком,
∑δ β = − fβ . |
(30) |
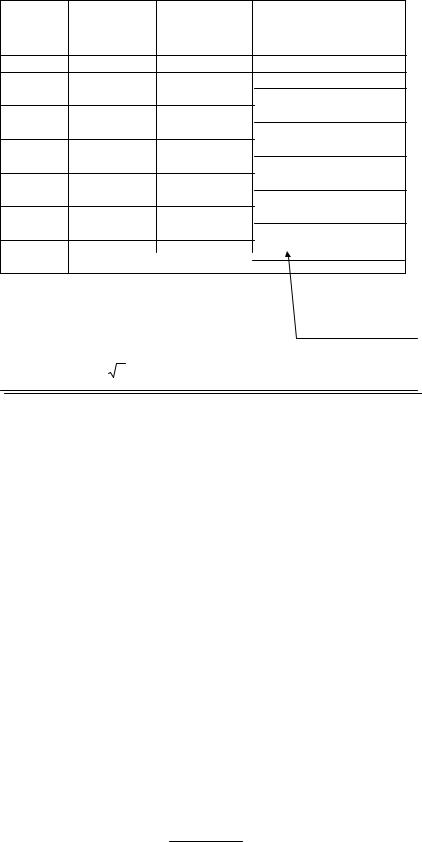
Поправки вводятся в измеренные углы, в табл. 5 поправки записаны над значениями измеренных углов, колонка 2.
|
|
βИСПР = βИЗМ + δβ. |
|
(31) |
|
Правильность введения поправок контролируется условием |
|||||
|
|
|
ΣβИСП = ΣβТЕОР; |
(32) |
|
Таблица 5 - Фрагмент ведомости вычисления координат |
|
||||
№ |
Измерен. |
Исправленные |
Дирекцион |
Расстоян |
|
точки |
|
углы |
углы |
углы |
|
1 |
|
2 |
3 |
4 |
5 |
1 |
|
|
|
135 54.0 |
130.00 |
|
|
+0.5 |
|
||
2 |
54 32 |
54 32.5 |
10 26.5 |
93.50 |
|
|
|
+0.5 |
|
||
3 |
108 33 |
108 33.5 |
299 00.0 |
78.54 |
|
|
|
+0.5 |
|
||
4 |
107 20 |
107 20.5 |
226 20.5 |
53.41 |
|
|
|
+0.5 |
|
||
1 |
89 33 |
89 33.5 |
135 54.0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Σβ |
п о л |
= 359O58′ |
360 00.0 |
Контроль - |
|
|
|
|
|
|
|
Σβтеор = 360O |
|
|
|
||
f β = −1.0′ |
|
|
|
||
f βдоп = 1′ n |
|
|
|
||
Проконтролировав правильность введения поправок в измеренные углы, вычисляются дирекционные углы
α = α 0 |
+ β ле в |
±180 O ; |
α = α 0 |
|
(33) |
− β п рав ±180 O , |
||
где β ле в, βп рав - соответственно, леволежащие и праволежащие по ходу исправ-
ленные горизонтальные углы.
Контроль - вычисленный по ходу дирекционный угол исходной стороны должен быть равен исходному дирекционному углу данной стороны.
Следующий этап вычислений это вычисление приращений координат
X = S cos α;
(34)
Y = S sin α,
при вычислении приращений координат следует обратить внимание на знаки приращений, они соответствуют знакам функций синус и косинус дирекционных углов; для контроля можно воспользоваться следующими соотношениями.
если 0 < α < 90O , то X > 0 , Y > 0 ;
если |
90 O < α < 180 O , то |
X < 0 , |
Y > 0 ; |
если |
180 O < α < 270 O , то |
X < 0 , |
Y < 0 ; |
если |
270 O < α < 360 O , то |
X > 0 , |
Y < 0 . |
Числовое значение приращений контролируется теоремой Пифагора
S = 
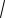 X 2 + Y 2 .
X 2 + Y 2 .

Вычисленные приращения координат записываются в колонки 6,7 ведомости вычисления координат, фрагмент ведомости
с вычисленными приращениями приведен в табл. 5. |
|
|
4 |
|||||||||
|
|
|
|
|||||||||
Сумма приращений |
|
координат позволяет |
|
|
|
|
||||||
осуществить контроль качества линейных измере- |
1’ |
3 |
||||||||||
ний. Если в измеренных линиях есть ошибки, то |
|
|
||||||||||
fX |
|
fS |
||||||||||
последняя точка теодолитного хода не совпадет с |
|
|
|
|||||||||
исходной, рис. 9, |
т.е. |
образуется абсолютная ли- |
|
fY |
1 |
|||||||
|
|
|||||||||||
нейная невязка fS |
по которой осуществляется кон- |
|
|
2 |
||||||||
троль качества линейных измерений |
|
|
||||||||||
Рис. 9. Образование абсолют- |
||||||||||||
|
|
f S |
≤ |
|
1 |
|
, |
|||||
|
|
|
|
|
ной линейной невязки |
|||||||
|
|
S |
|
|
|
|
||||||
|
|
2000 |
|
|
||||||||
где S - длина теодолитного хода ( для замкнутого хода - периметр полигона)
Таблица 6 - Фрагмент ведомости вычисления координат
|
|
|
|
|
|
|
|
Выч. приращения |
Испр. приращения |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
координат |
координат |
|
|
|||||
|
|
|
|
|
|
|
|
X |
|
|
Y |
X |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
6 |
|
7 |
|
8 |
9 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+5 |
|
-2 |
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
-93.36 |
|
+ 90.47 |
|
-93.31 |
+90.45 |
|
|
|
|
|
|
|
|
|
+5 |
|
-2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
+91.95 |
|
+16.94 |
+92.00 |
+16.92 |
|
|
||
|
|
|
|
|
|
+5 |
|
-2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
4 |
|
|
|
|
|
+38.08 |
|
-68.69 |
|
+38.13 |
-68.71 |
|
|
|
|
|
|
|
|
|
+5 |
|
-2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
-36.87 |
|
-38.64 |
|
-36.82 |
-38.66 |
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контроль |
|
|
ΣΔX=-0.20 ΣΔY=+0.08 ΣΔX=0.0 |
ΣΔY=+0.0 |
||||||||||
|
|
|
|
|
|
|
f X =-0.20 |
|
f Y =+0.08 |
|
|
|
|
|||
Согласно рис. 9 абсолютная линейная невязка равна |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
, |
|
|
|||
|
|
|
|
|
|
|
|
f S |
f X2 + fY2 |
|
(35) |
|||||
где fX, fY - соответственно, невязки в приращениях координат
Для замкнутого теодолитного хода теоретическая сумма приращений координат равна нулю, следовательно, невязки в приращениях координат равны
|
|
|
|
f X |
= ∑ X , |
|
|
|
||
|
|
|
|
f y |
= ∑ Y ; |
|
|
|
||
|
Контроль качества теодолитного хода осуществляется по допуску |
|
||||||||
|
|
|
|
|
|
f S |
≤ |
1 |
, |
(36) |
|
|
|
|
|
|
|
2000 |
|||
|
|
|
|
|
|
S |
|
|
||
где |
f S |
= |
1 |
; P - периметр полигона. |
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|||
|
S |
|
|
|
|
|
|
|
||
|
|
|
f S |
|
|
|
|
|
|
|
