Дополнительный код
Дополнительным называется код, в котором для положительного числа в знаковом разряде пишется "0", в цифровых - модуль числа, а для отрицательного в знаковом разряде пишется "1", в цифровых - дополнение числа до единицы.
Если некоторое X- = -0,x1x2...xn нужно представить в дополнительном коде, то
где: 1 - 0,x1x2...xn = 0, Z1Z2...Zn
Диапазоны представленных чисел:
Х+ min = 0,0...0 - положительный нуль
Х+ max = 0,11...1 = 1-2-n - максимальное положительное число.
X- min = 1,11...1 = 2-2-n - минимальное отрицательное число
X- max = 1,0...0 - наибольшее(по модулю) отрицательное число
Таким образом, нуль имеет единственное представление.
В самом деле, так как
X-X = [X+]дк + [X-]дк = 0, то в дополнительном коде: |X+| + 10 - |X-| = 10, если в разрядной сетке ЭВМ нет второго знакового разряда, то это переполнение теряется, и в знаковом разряде будет только нуль.
Важная особенность в получении дополнительного кода отрицательного числа состоит в следующем:
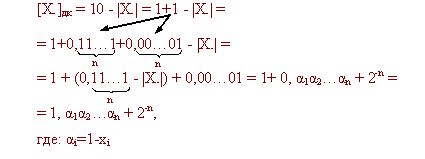
Таким образом, для записи дополнительного кода отрицательного числа необходимо в знаковом разряде поставить единицу, проинвертировать все цифровые разряды числа и прибавить единицу в младший разряд. Это также правило перевода из дополнительного кода в прямой код.
Рассмотрим на примерах выполнение операции сложения двух чисел с разными знаками.
Возможны следующие случаи:
X+ + Y+ = S+
X+ + Y- = S+
X+ + Y- = S-
X- + Y- = S-
Необходимо помнить, что нельзя, выполняя операции, выходить за диапазон представляемых в данной разрядной сетке чисел, записанных сфиксированной запятой.
Положим n = 3, 1 - знаковый разряд и 2 - цифровых.
X+ = 0,10
Y+ = 0,01
В дополнительном коде
То есть, нет никаких особенностей.
X+ = 0,10
Y- = -0,01
В дополнительном коде
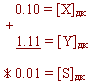
Переполнение теряется и получается верный результат.
X+ = 0,01
Y- = -0,11
В дополнительном коде
X- = -0,10
Y- = -0,01
В дополнительном коде
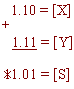
Возникающее переполнение теряется и общий результат отрицательный.
Таким образом, важной особенностью дополнительного кода является то, что знаковый разряд в процессе выполнения операции рассматривается совместно с цифровыми. Возникающие переносы теряются и не влияют на результат операции.
Обратный код
Обратным называется код, для которого в знаковом разряде положительного числа пишется "0", в цифровых - модуль числа, а для отрицательного - в знаковом разряде пишется единица, в цифровых - инвертированные разряды исходного числа.
Определим диапазоны чисел:
X+ min = 0,00...0 - положительный нуль.
X+ max = 0,111...1 = 1 - 2-n
X- min = 1,11...1 0 = 2 - 2-n+1
X- max = 1,00...00 = 1
В обратном коде есть два изображения нуля:
"Положительный" нуль:
[X]ок = 0,0...0
и "отрицательный" нуль:
[X]ок = 1,11...11
При этом
X - X = [X+]ок + [X-]ок = |X+| + 10 - (10)-n - |X-| = +10 - (10)-n = 0
То есть, единица переноса в знаковом разряде эквивалентна единице младшего разряда. Поэтому при выполнении операции сложения-вычитания необходимо возникающий перенос циклически прибавлять в младший разряд частичного результата.
Рассмотрим прежние четыре случая, помня о том, что сумма двух слагаемых по модулю должна быть меньше единицы.
X+ = 0,10
Y- = -0,01
X+ + Y- = S+
В обратном коде:
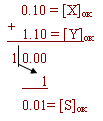
Возникающее переполнение должно быть добавлено к младшему разряду частичной суммы.
X+ = 0,10
Y+ = +0,01
X+ + Y+ = S+
В обратном коде:
Нет никаких особенностей по сравнению с прямым кодом.
X+ = 0,01
Y- = -0,10
X+ + Y- = S-
В обратном коде:
То есть, не возникает циклического переноса.
X- = -0,01
Y- = -0,10
X- + Y- = S-
В обратном коде:
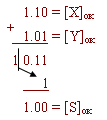
Возникает переполнение знакового разряда, которое добавляется в младший разряд частичной суммы.
Заметим, что получение обратного кода проще, чем дополнительного. Это поразрядно выполняемая микрооперация инверсии кода. Как станет ясно из схемного решения, эта микрооперация выполняется так же быстро, как и передача кода.
Поскольку результатом операции является совокупность результатов по всем разрядам, то данную операцию можно выполнять одновременно над всеми цифровыми разрядами числа.